Mean Value Theorem
Mean Value Theorem is an important theorem in calculus. The first form of the mean value theorem was proposed in the 14th century by Parmeshwara, a mathematician from Kerela, India. Further, a simpler version of this was proposed by Rolle in the 17th century: Rolle's Theorem, which was proved only for polynomials and was not a part of the calculus. Finally, the present version of the Mean Value Theorem was proposed by Augustin Louis Cauchy in the year 1823.
The mean value theorem states that for a curve passing through two given points there is one point on the curve where the tangent is parallel to the secant passing through the two given points. Rolle's theorem has been derived from this mean value theorem.
| 1. | What Is Mean Value Theorem? |
| 2. | Mean Value Theorem Proof |
| 3. | Graphical Representation of Mean Value Theorem |
| 4. | Difference Between Mean Value Theorem and Rolle's Theorem |
| 5. | FAQs on Mean Value Theorem |
What is Mean Value Theorem?
The mean value theorem states that for any function f(x) whose graph passes through two given points (a, f(a)), (b, f(b)), there is at least one point (c, f(c)) on the curve where the tangent is parallel to the secant passing through the two given points. The mean value theorem is defined herein calculus for a function f(x): [a, b] → R, such that it is continuous and differentiable across an interval.
- The function f(x) is continuous over the interval [a, b].
- The function f(x) is differentiable over the interval (a, b).
- There exists a point c in (a, b) such that f'(c) = [ f(b) - f(a) ] / (b - a)
Here we have proved that the tangent at c is parallel to the secant passing through the points (a, f(a)), (b, f(b)). This mean value theorem is used to prove a statement across a closed interval. Further, the mean value theorem is derived from the Rolle's theorem.
Mean Value Theorem Proof
Statement: The mean value theorem states that if a function f is continuous over the closed interval [a, b], and differentiable over the open interval (a, b), then there exists at least one point c in the interval (a, b) such that f '(c) is the average rate of change of the function over [a, b] and it is parallel to the secant line over [a, b].
Proof: Let g(x) be the secant line to f(x) passing through (a, f(a)) and (b, f(b)). We know that the equation of the secant line is y - y1 = m (x - x1).
g(x) - f(a) = [ f(b) - f(a) ] / (b - a) (x-a)
g(x) = [ f(b) - f(a) ] / (b - a) (x-a) + f(a) ----->(1)
Let h(x) be f(x) - g(x)
h(x) = f(x) - [[ f(b) - f(a) ] / (b - a) (x-a) + f(a)] (From (1))
h(a) = h(b) = 0 and h(x) is continuous on [a, b] and differentiable on (a, b).
Thus applying the Rolles theorem, there is some x = c in (a, b) such that h'(c) = 0.
h'(x) = f'(x) - [ f(b) - f(a) ] / (b - a)
For some c in (a, b), h'(c) = 0. Thus
h'(c) = f'(c) - [ f(b) - f(a) ] / (b - a) = 0
f'(c) = [ f(b) - f(a) ] / (b - a)
Thus the mean value theorem is proved.
Note: The result may not hold if the function is not differentiable, even at a single point in the open interval.
Graphical Representation of Mean Value Theorem
The graphical representation of the function f(x) helps in understanding the mean value theorem. Here we consider two distinct points (a, f(a)), (b, f(b)). The line connecting these points is the secant of the curve, which is parallel to the tangent cutting the curve at (c, f(c)). The slope of the secant of the curve joining these points is equal to the slope of the tangent at the point (c, f(c)). We know that the derivative of the tangent is the slope at that point.
Slope of the Tangent = Slope of the Secant
f'(c) = [ f(b) - f(a) ] / (b - a)
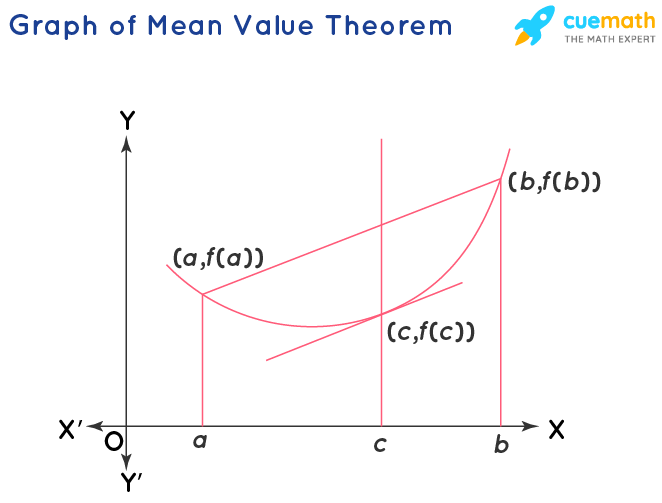
Here we observe that the point (c, f(c)), lies between the two points (a, f(a)), (b, f(b)).
Difference Between Mean Value Theorem and Rolle's Theorem
Both the mean value theorem and Rolle's theorem define the function f(x) such that it is continuous across the interval [a, b], and it is differentiable across the interval (a, b). In the mean value theorem, the two referred points (a, f(a)), (b, f(b)) are distinct and f(a) ≠ f(b). In Rolle's theorem, the points are defined such that f(a) = f(b).
The value of c in the mean value theorem is defined such that the slope of the tangent at the point (c, f(c)) is equal to the slope of the secant joining the two points. The value of c in Rolle's theorem is defined such that the slope of the tangent at the point (c, f(c)) is equal to the slope of the x-axis. The slope in the mean value theorem is f'(c) = [ f(b) - f(a) ] / (b - a), and the slope in Rolle's theorem is equal to f'(c) = 0.
☛Related Topics:
FAQs on Mean Value Theorem
What Does the Mean Value Theorem State?
The mean value theorem states that if a function f is continuous over the closed interval [a, b], and differentiable over the open interval (a, b), then there exists a point c in the interval (a, b) such that f'(c) is the average rate of change of the function over [a, b] and it is parallel to the secant line over [a, b].
What is the Mean Value Theorem Equation?
The mean value theorem is defined for a function f(x): [a, b]→ R, such that it is continuous in the interval [a, b], and differentiable in the interval (a, b). For a point c in (a, b), the equation for the mean value theorem is as follows: f'(c) = [ f(b) - f(a) ] / (b - a)
What is the Difference Between Rolle's Theorem and Mean Value Theorem?
If f(x) is a function that is continuous on [a, b] and differentiable on (a, b),
- and if f(a) = f(b), then by Rolle's theorem, then there exists a 'c' in the interval (a, b) such that f'(c) = 0.
- then by mean value theorem, there exists a 'c' in the interval (a, b) such that f'(c) = [ f(b) - f(a) ] / (b - a).
What Does Mean Value Theorem Mean?
The mean value theorem states that for a curve passing through two given points there is one point on the curve where the tangent is parallel to the secant passing through the two given points. Rolle's theorem is used to derive the mean value theorem.
What is the Hypothesis of the Mean Value Theorem?
The hypothesis for the mean value theorem is that, for a continuous function f(x), it is continuous in the interval [a, b], and it is differentiable in the interval (a, b).
How to Find the Values that Satisfy Mean Value Theorem?
The values satisfying the mean value theorem are calculated by finding the differential of the given function f(x). The given function is defined in the interval (a, b), and the value satisfying the mean value theorem is the point c, which belongs to the interval (a, b). And we can find its value from f'(c) = [ f(b) - f(a) ] / (b - a)
How to Derive Rolle's Theorem From Mean Value Theorem?
Consider a function f(x) that is continuous on [a, b] and differentiable on (a, b). Then by mean value theorem, there exists a 'c' such that f'(c) = [ f(b) - f(a) ] / (b - a). To derive Rolle's theorem from this, let us take the additional condition in the hypothesis of Rolle's theorem that f(a) = f(b). Substituting this in the above equation, f'(c) = [ f(a) - f(a) ] / (b - a) = 0 and hence the Rolle's theorem is proved.
What is the Difference Between Mean Value Theorem and Intermediate Value Theorem?
If f(x) is continuous on [a, b] and differentiable on (a, b),
- then by mean value theorem, there exists a 'c' in the interval (a, b) such that f'(c) = [ f(b) - f(a) ] / (b - a).
- then by intermediate value theorem, for any L between f(a) and f(b), there exists a 'c' in the interval (a, b) such that f(c) = L.
How to Find C for Mean Value Theorem in Integrals?
As per the mean value theorem for the function f(x) defined in the interval (a, b), the value of C belongs to (a, b), and is calculated using the slope of the secant connecting the points (a, f(a)), (b, f(b)). The value of c is calculated from the derivative formula of f'(c) = [ f(b) - f(a) ] / (b - a)
What is the Difference Between Mean Value Theorem and Cauchy's Mean Value Theorem?
If f(x) and g(x) are two continuous functions over [a, b] and differentiable over (a, b) then:
- according to mean value theorem, ∃ c ∈ (a, b) such that f'(c) = [ f(b) - f(a) ] / (b - a).
- according to Cauchy's mean value theorem, ∃ c ∈ (a, b) such that f'(c) / g'(c) = [ f(b) - f(a) ] / [ g(b) - g(a) ], where g'(x) ≠ 0, ∀ x ∈ (a, b).