Intermediate Value Theorem
The intermediate value theorem (IVT) in calculus states that if a function f(x) is continuous over an interval [a, b], then the function takes on every value between f(a) and f(b). This theorem has very important applications like it is used:
- to verify whether there is a root of a given equation in a specified interval.
- to verify the existence of x-intercept of a function over a given interval, etc.
Let us learn more about the intermediate value theorem along with its proof and limitations along with examples.
| 1. | What is Intermediate Value Theorem? |
| 2. | Intermediate Value Theorem Proof |
| 3. | Application of Intermediate Value Theorem |
| 4. | Limitations of IVT Theorem |
| 5. | FAQs on Intermediate Value Theorem |
What is Intermediate Value Theorem?
The intermediate value theorem (also known as IVT or IVT theorem) says that if a function f(x) is continuous on an interval [a, b], then for every y-value between f(a) and f(b), there exists some x-value in the interval (a, b). i.e., if f(x) is continuous on [a, b], then it should take every value that lies between f(a) and f(b). Recall that a continuous function is a function whose graph is a curve that can be drawn without lifting a pencil. Mathematically, this theorem is stated as follows:
Intermediate Value Theorem: "Suppose f(x) is a continuous function on [a, b] and L is a number that lies between f(a) and f(b), then there exists at least one 'c' such that c ∈ (a, b) (or a < c < b) and f(c) = L"
It is so obvious (because of continuity) how the theorem works and we can understand it from the following figure.
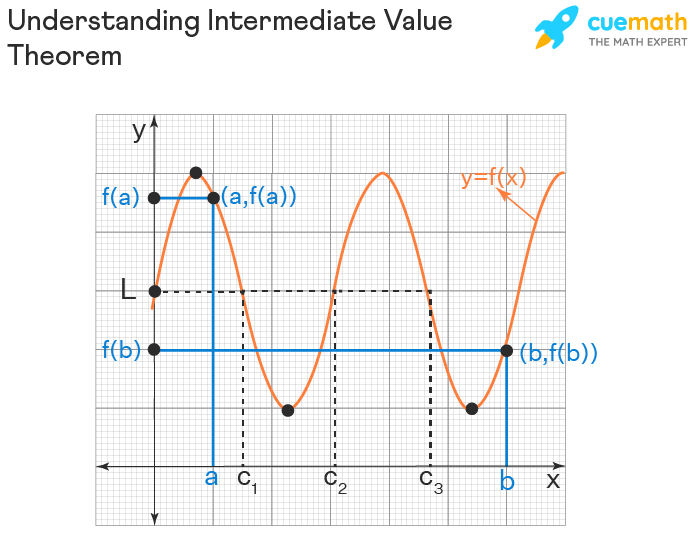
When the graph of f(x) can be drawn without lifting a pencil within the interval [a, b], it is so obvious that f(x) takes every value L that lies between f(a) and f(b). In fact, it is also possible that the equation f(c) = L can be possible for more than one value of 'c'. In the above figure, it is pretty clear that:
- f(c1) = L
- f(c2) = L
- f(c3) = L
It means that there are three values c1, c2, and c3 in the interval [a, b] whose function value is L.
Intermediate Value Theorem Proof
Though the proof of the intermediate value theorem is so pretty straight forward as mentioned earlier, here is the mathematical proof of the IVT theorem using the limit definition. Without loss of generality, assume that f(a) < L < f(b) and consider the following set:
A = { x ∈ [a, b]: f(x) < L}.
Notice that A is non-empty as a ∈ A (as f(a) < L) and also A is bounded above by 'b'.
Then it must have a supremum and let us assume it to be 'c'.
Proving c ∈ (a, b)
Because of the continuity of the function f(x) at 'a' and 'b', f(c) ≠ a and f(c) ≠ b.
Thus, c ∈ (a, b).
Proving f(c) = L
For this, we prove both f(c) ≤ L and f(c) ≥ L.
Proof of f(c) ≤ L:
Since 'c' is the supremum, by extreme value theorem, there is a sequence xn ∈ A with xn → c.
Since f(x) is continuous, f(xn) → f(c).
But xn ∈ A, and by definition of A, f(xn) < L.
⇒ f(c) = limn → ∞ f(xn) ≤ L.
Thus, we proved that f(c) ≤ L ... (1)
Proof of f(c) ≥ L:
Notice that c < b. Thus, for a very small 'n', tn = c + (1/n) < b.
Again, tn > c ⇒ tn > supremum of A. Thus, tn ∉ A.
Thus, f(tn) ≥ L.
Since 'n' is very small and f(x) is continuous, f(tn) → f(c). From this,
f(c) = limn → ∞ f(tn) ≥ L ... (2)
From (1) and (2), we have can conclude that f(c) = L.
Thus, the intermediate value theorem is proved.
Application of Intermediate Value Theorem
The important application of the intermediate value theorem is to verify the existence of a root of an equation in a given interval. In particular, the IVT theorem is used to see whether a given function has its zero (x-intercept (or) f(x) = 0) within the given interval (a, b). To verify this, we follow the steps below:
- Step 1: Find f(a) and f(b).
- Step 2: If f(a) < 0 < f(b) (i.e., f(a) is negative and f(b) is positive) then f(x) has a zero (i.e., f(x) = 0) in the interval (a, b).
Let us examine the following example.
Example: Use the IVT to verify whether the function f(x) = x3 - 3x - 19 has a zero in the interval [1, 5].
Solution:
The interval is [1, 5]. Find f(1) and f(5).
f(1) = 13 - 3(1) - 19 = -21
f(5) = 53 - 3(5) - 19 = 91
Since f(1) is positive and f(5) is negative, by the intermediate value theorem, we can say that there must be some 'c' in [1, 5] such that f(c) = 0.
i.e., f(x) has a zero in the interval [1, 5].
Limitations of IVT Theorem
Observe the above example. Using the intermediate value theorem, we could only find whether the function f(x) has a root in the interval [1, 5]. But we couldn't find what root it is. Also, we couldn't verify how many roots f(x) has within the given interval (as we have seen in the figure of the first section, the function can take a value for more than one value of x). Further, there is one more limitation of the IVT theorem which can be understood from the example below:
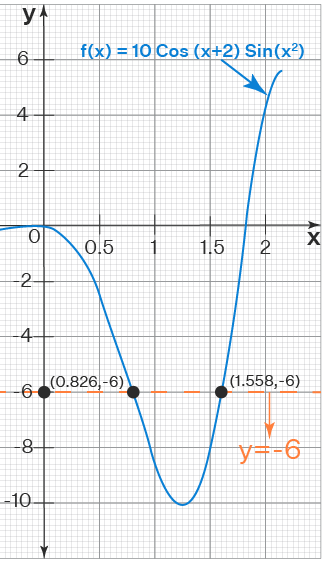
Example: Use the intermediate value theorem to verify whether the equation 10 cos (x + 2) sin (x2) = -6 has a root in the interval [0.5, 2]?
Solution:
Let f(x) = 10 cos (x + 2) sin (x2).
The given interval is [0.5, 2]. So we will find f(0.5) and f(2).
f(0.5) = 10 cos (0.5 + 2) sin (0.52) = -1.98
f(2) = 10 cos (2 + 2) sin (22) = 4.95
We wanted to know whether f(x) = -6 has a solution in the given interval. We can see that -6 does NOT lie between -1.98 and 4.95. What do the values of f(0.5) and f(2) tell about the existence of the root of f(x) = -6 in the given interval? Unfortunately, the intermediate value theorem does not mean anything in this case. This theorem can guarantee only whether the function takes the value, but it cannot guarantee about a value that a function cannot take.
Thus, in the above example, we cannot say using the IVT theorem that f(x) = -6 does NOT have a root in the interval [0.5, 2]. In fact, it has two roots (0.826 and 1.558) in the given interval as shown in the graph below.
Important Notes on Intermediate Value Theorem:
- Using the intermediate value theorem, we can just know if the root exists; but it cannot guarantee if the root does not exist (see the above example).
- The IVT theorem cannot be applied when the function is NOT continuous.
- It does not help in finding the roots of an equation.
- We cannot say how many roots the equation has in the given interval using this theorem.
☛ Related Topics:
Intermediate Value Theorem Examples
-
Example 1: Use the intermediate value theorem to verify whether a function f(x) = x + 1/x has a zero in the interval [-1, 1]?
Solution:
The first condition to apply the IVT theorem is the function should be continuous in the given interval.
But the given function f(x) = x + 1/x is NOT continuous over [-1, 1] as f(0) is NOT defined here.
Thus, we cannot apply IVT here.
Answer: IVT cannot be applied here.
-
Example 2: Does the equation x4 + 3x2 - 2 = 0 has a solution in the interval [0, 1]? Explain your reasoning using IVT theorem.
Solution:
Let us assume that f(x) = x4 + 3x2 - 2.
Since f(x) is a polynomial function, it is continuous.
We will find f(0) and f(1).
f(0) = 04 + 3(0)2 - 2 = -2
f(1) = 14 + 3(1)2 - 2 = 2
We want to know whether f(x) = 0 has any roots in the given interval. i.e., we have to see whether the function takes in the value 0. It is clear that -2 < 0 < 2 and hence by the intermediate value theorem, the given equation has at least one root in the given interval.
Answer: Yes, it has a root in [0, 1].
-
Example 3: Support your answer for Example 2 by graphing it.
Solution:
In Example 2, we have already proved by IVT that the given equation has a root in [0, 1]. Let us graph f(x) = x4 + 3x2 - 2 and see whether it has any roots (i.e., see whether it intersects the x-axis).

Since the graph cuts the x-axis at (0.749, 0), 0.749 is a root of the given function and it lies in the interval [0, 1].
Answer: The existence of the root is verified using the graph.

FAQs on Intermediate Value Theorem
What is IVT Calculus?
IVT (Intermediate Value Theorem) in calculus states that a function f(x) that is continuous on a specified interval [a, b] takes every value that is between f(a) and f(b). i.e., for any value 'L' lying between f(a) and f(b), there exists at least one value c such that a < c < b and f(c) = L.
How Do You Know When to Use Intermediate Value Theorem?
If we want to know whether a function has a root in the given interval, then we can use the intermediate value theorem. Note that this theorem only when the function is continuous.
Can the IVT Theorem be Applied for Discontinuous Functions?
No, the intermediate value theorem cannot be applied for discontinuous functions. Because "continuity" is what is making a function f(x) on an interval [a, b] to take any value between f(a) and f(b).
What are the Conditions of the Intermediate Value Theorem?
The conditions of IVT to apply on a function f(x) over an interval [a, b] are:
- f(x) should be continuous on [a, b]
- f(a) ≠ f(b)
When Cannot We Use Intermediate Value Theorem?
The intermediate value theorem :
- says "yes the function takes a value" if it really takes
- but it cannot say "no the function doesn't take a value" if it doesn't take
Thus, for a function f(x) that is continuous on [a, b], if a value L does not lie between f(a) and f(b), it is not always true that there is no value such that f(c) = L. Sometimes, there can be values of 'c' satisfying f(c) = L.
How Can We Find Zeros Using IVT Theorem?
IVT theorem is used just to verify if the function has a zero in the given interval. But it is neither used in finding the number of zeros nor used in finding the number of zeros.
What is the Difference Between Mean Value Theorem and Intermediate Value Theorem?
The mean value theorem talks about the differentiable and continuous functions and the intermediate value theorem talks only about the continuous functions. For more information, click here.
visual curriculum