Average Rate of Change Formula

The average rate of change describes the average rate at which one quantity is changing with respect to another. It gives an idea of how much the function changed per unit in the given interval. In simple terms, in the rate of change, the amount of change in one item is divided by the corresponding amount of change in another. Let's look into the average rate of change formula in detail.

What is the Average Rate of Change?

The average rate of change of a function f(x) over an interval [a, b] is defined as the ratio of "change in the function values" to the "change in the endpoints of the interval". i.e., the average rate of change can be calculated using [f(b) - f(a)] / (b - a). In other words, the average rate of change (which is denoted by A(x)) is the "ratio of change in outputs to change in inputs". i.e.,

A(x) = (change in outputs) / (change in inputs)

= Δy / Δx

= [f(b) - f(a)] / (b - a)

Here, Δy is the change in y-values (or) change in the function values and Δx is the change in x-values (or) the change in the endpoints of the interval. Some examples of the average rate of change are:

• A bus travels at a speed of 80 km per hour.
• The number of fish in a lake increases at the rate of 100 per week.
• The current in an electrical circuit decreases 0.2 amperes for a decrease of 1-volt voltage.

Average Rate of Change Formula

The average rate of change function describes the average rate at which one quantity is changing with respect to something another quantity. The average rate of change formula is given as,

A(x) = [f(b) - f(a)] / (b - a)

where,

• A(x) = Average rate of change
• f(a) = Value of function f(x) at a
• f(b) = Value of function f(x) at b

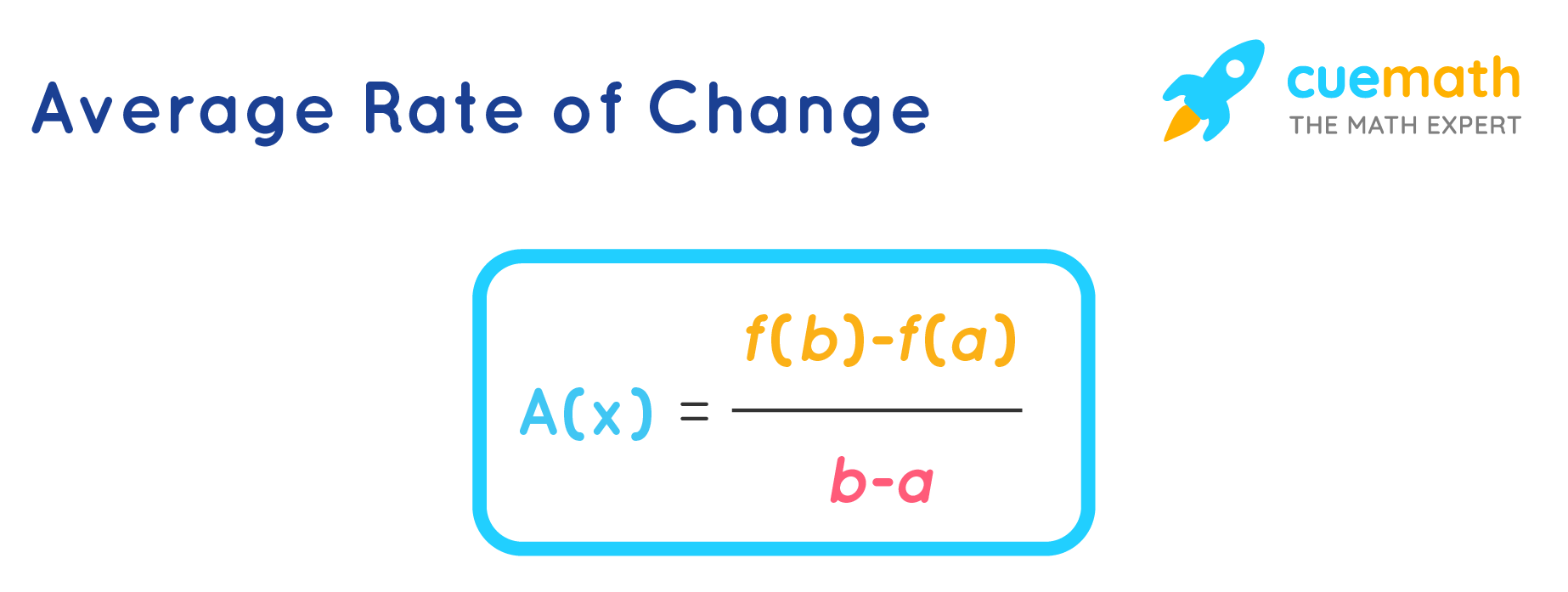
Examples Using Average Rate of Change Formula

Example 1: Calculate the average rate of change of a function, f(x) = 2x + 10 as x changes from 3 to 7.

Solution:

Given:

f(x) = 2x + 10, a = 3, b = 7.

• f(3) = 2(3) + 10 = 6 + 10 = 16
• f(7) = 2(7) + 10 = 14 + 10 = 24

Using the average rate of change formula,

A(x) = [f(b)−f(a)] / (b−a)

A(x) = [f(7)−f(3)]/ (7−3)

A(x) = (24 - 16) / 4

A(x) = 8/4

A(x) = 2

Therefore, the rate of change is 2.

Example 2: Evaluate the average rate of change of the function f(x) = x² – 5x in the interval 4 ≤ x ≤ 8.

Solution:

Given: f(x) = x² – 5x, a = 4, b = 8.

• f(4) = f(4) = (4)² – 5(4) = 16 – 20 = -4
• f(8) = f(8) = (8)² – 5(8) = 64 – 40 = 24

Using the average rate of change formula,

A(x) = [f(b)−f(a)] / (b−a)

= (24−(−4)) / (8−4)

= 28/4

= 7

Therefore, rate of change A(x) = 7.

Example 3: Find the rate of change of a function, f(x) = 25x + 18 as x changes from 5 to 8

Solution: Given,

f(x) = 25x + 18, a = 5 and b = 8

• f(5) = 25×5 + 18 = 143
• f(8) = 25×8 + 18 = 218

Using the average rate of change formula,

A(x) = [f(b)−f(a)] / (b−a)

= [218 - 143] / (8 - 5)

= 75 / 3

= 25

Therefore, the average rate of change A(x) = 25