Slope of the Secant Line Formula

Before going to learn the slope of the secant line formula, let us recall what is slope and what is a secant. The slope of a line is defined as rise over run. A secant line of a curve is a line that passes through any two points of the curve. When one of these points is approaching the other, then the slope of the secant line would become the slope of the tangent line at that particular point. Let us learn more about the slope of the secant line formula in the upcoming sections.

What Is the Slope of the Secant Line Formula?

We use the slope of a line formula to find the slope of a secant line formula because secant line is also a line. There are multiple formulas to find the slope of a secant line depending on the available information. Let us consider a curve y = f(x) and consider a secant line drawn to this curve. 

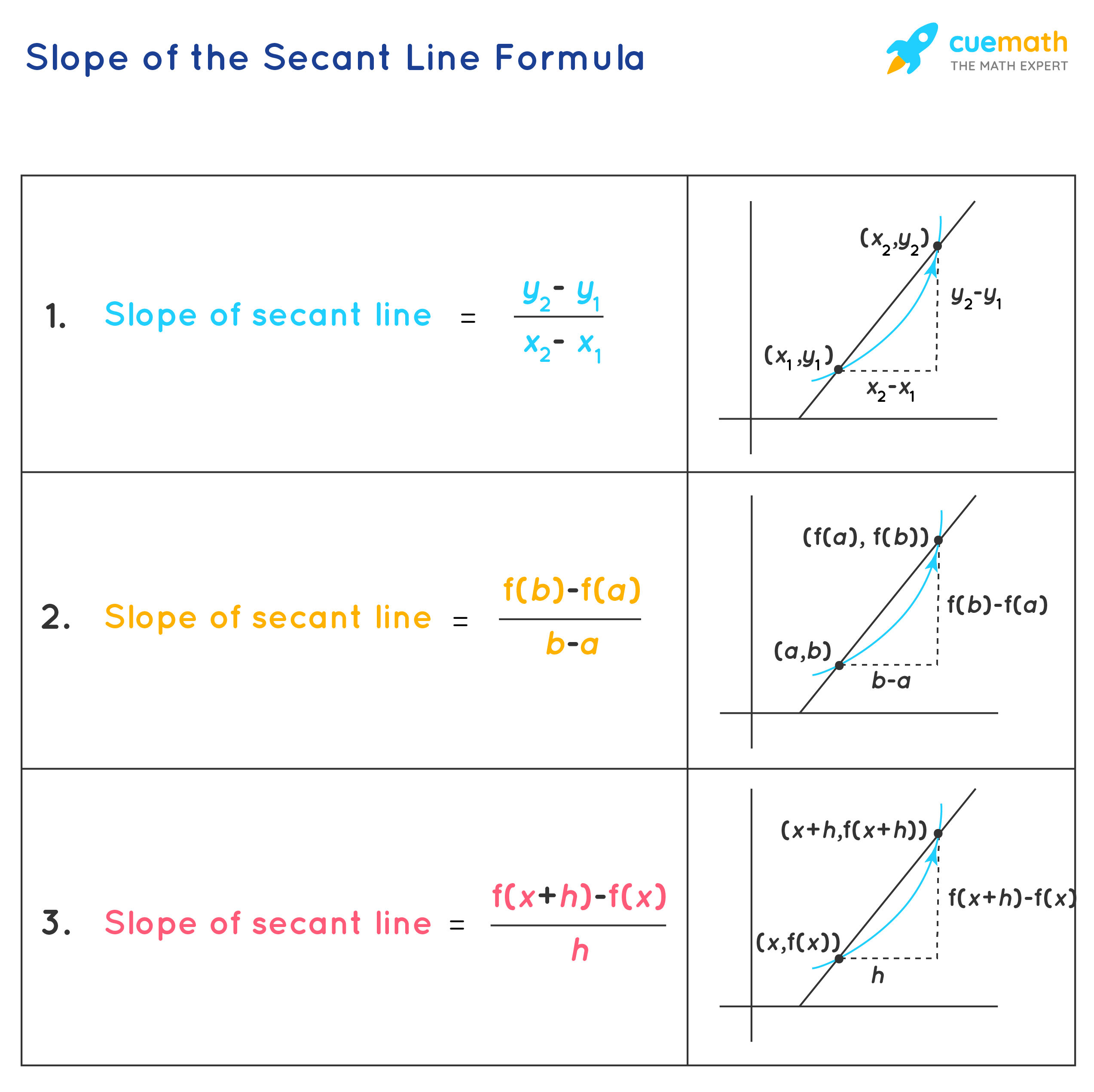
• If \((x_1,y_1)\) and \((x_2,y_2)\) are two points on the curve y = f(x) through which the secant line is passing, then:

  Slope of the secant line = \(\dfrac{y_2-y_1}{x_2-x_1}\)

• If the secant line is passing through two points (a, f(a)) and (b, f(b)), then:

  Slope of the secant line = \(\dfrac{f(b)-f(a)}{b-a}\)

  This is also referred to as "average rate of change of f(x)" from x = a to x = b.

• If the secant line is passing through two points P and Q, where P = (x, f(x)) and Q = (x + h, f(x + h)), then:

  Slope of the secant line = \(\dfrac{f(x+h)-f(x)}{x+h-x}\) = \(\dfrac{f(x+h)-f(x)}{h}\)

  Here, \(\dfrac{f(x+h)-f(x)}{h}\) is also referred to as "difference quotient".

Note: The slope of the secant line formula gives the slope of the tangent line formula (which is also nothing but the derivative of the function at that point) when \(x_2 \rightarrow x_1\), (or) b → a, (or) h → 0.

Let us have a look at a few solved examples to understand secant line formula better.