Logarithmic Functions

The logarithmic function is an important medium of math calculations. Logarithms were discovered in the 16^th century by John Napier a Scottish mathematician, scientist, and astronomer. It has numerous applications in astronomical and scientific calculations involving huge numbers. Logarithmic functions are closely related to exponential functions and are considered as an inverse of the exponential function. The exponential function a^x = N is transformed to a logarithmic function log_aN = x.

The logarithm of any number N if interpreted as an exponential form, is the exponent to which the base of the logarithm should be raised, to obtain the number N. Here we shall aim at knowing more about logarithmic functions, types of logarithms, the graph of the logarithmic function, and the properties of logarithms.

The basic logarithmic function is of the form f(x) = log_ax (r) y = log_ax, where a > 0. It is the inverse of the exponential function a^y = x. Log functions include natural logarithm (ln) or common logarithm (log). Here are some examples of logarithmic functions:

• f(x) = ln (x - 2)
• g(x) = log₂ (x + 5) - 2
• h(x) = 2 log x, etc.

Some of the non-integral exponent values can be calculated easily with the use of logarithmic functions. Finding the value of x in the exponential expressions 2^x = 8, 2^x = 16 is easy, but finding the value of x in 2^x = 10 is difficult. Here we can use log functions to transform 2^x = 10 into logarithmic form as log₂10 = x and then find the value of x. The logarithm counts the number of occurrences of the base in repeated multiples. The formula for transforming an exponential function into a logarithmic function is as follows.

The exponential function of the form a^x = N can be transformed into a logarithmic function log_aN = x. The logarithms are generally calculated with a base of 10, and the logarithmic value of any number can be found using a Napier logarithm table. The logarithms can be calculated for positive whole numbers, fractions, decimals, but cannot be calculated for negative values.

Let us consider the basic (parent) common logarithmic function f(x) = log x (or y = log x). We know that log x is defined only when x > 0 (try finding log 0, log (-1), log (-2), etc using your calculator. You will come up with an error). So the domain is the set of all positive real numbers. Now, we will observe some of the y-values (outputs) of the function for different x-values (inputs).

• When x = 1, y = log 1 = 0
• When x = 2, y = log 2 = 0.3010
• When x = 0.2, y = -0.6990
• When x = 0.01, y = -2, etc

We can see that y can be either a positive or negative real number (or) it can be zero as well. Thus, y can take the value of any real number. Hence, the range of a logarithmic function is the set of all real numbers. Thus:

• The domain of log function y = log x is x > 0 (or) (0, ∞).
• The range of any log function is the set of all real numbers (R)

Example: Find the domain and range of the logarithmic function f(x) = 2 log (2x - 4) + 5.

Solution:

For finding domain, set the argument of the function greater than 0 and solve for x.

2x - 4 > 0
2x > 4
x > 2

Thus, domain = (2, ∞).

As we have seen earlier, the range of any log function is R. So the range of f(x) is R.

We have already seen that the domain of the basic logarithmic function y = log_a x is the set of positive real numbers and the range is the set of all real numbers. We know that the exponential and log functions are inverses of each other and hence their graphs are symmetric with respect to the line y = x. Also, note that y = 0 when x = 0 as y = log_a1 = 0 for any 'a'. Thus, all such functions have an x-intercept of (1, 0). A logarithmic function doesn't have a y-intercept as log_a0 is not defined. Summarizing all these, the graphs of exponential functions and logarithmic graph look like below.

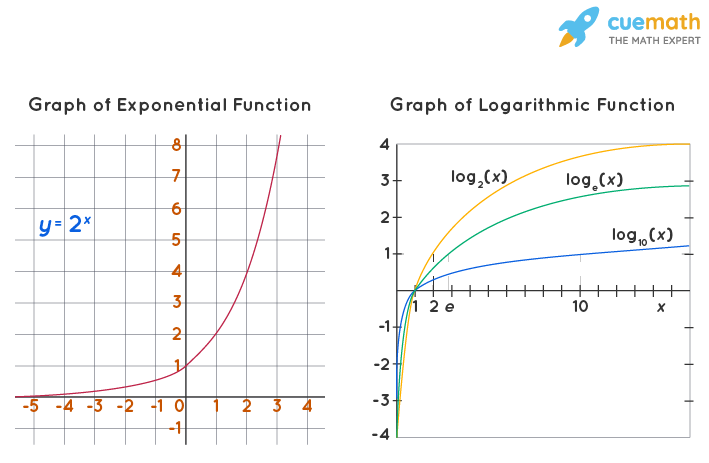
Properties of Logarithmic Graph

• a > 0 and a ≠ 1
• The logarithmic graph increases when a > 1, and decreases when 0 < a < 1.
• The domain is obtained by setting the argument of the function greater than 0.
• The range is the set of all real numbers.

Before drawing a log function graph, just have an idea of whether you get an increasing curve or decreasing curve as the answer. If the base > 1, then the curve is increasing; and if 0 < base < 1, then the curve is decreasing. Here are the steps for graphing logarithmic functions:

• Find the domain and range.
• Find the vertical asymptote by setting the argument equal to 0. Note that a log function doesn't have any horizontal asymptote.
• Substitute some value of x that makes the argument equal to 1 and use the property log_a 1 = 0. This gives us the x-intercept.
• Substitute some value of x that makes the argument equal to the base and use the property log_a a = 1. This would give us a point on the graph.
• Join the two points (from the last two steps) and extend the curve on both sides with respect to the vertical asymptote.

Example: Graph the logarithmic function f(x) = 2 log₃ (x + 1).

Solution:

Here, the base is 3 > 1. So the curve would be increasing.

For domain: x + 1 > 0 ⇒ x > -1. So domain = (-1, ∞).

Range = R.

Vertical asymptote is x = -1.

• At x = 0, y = 2 log₃ (0 + 1) = 2 log₃ 1 = 2 (0) = 0
• At x = 2, y = 2 log₃ (2 + 1)= 2 log₃ 3 = 2 (1) = 2

If we want more clarity, we can form a table of values with some random values of x and substitute each of them in the given function to compute the y-values. This way, we get more points on the graph and it helps in getting the perfect shape of the graph.

Thus, (0, 0) and (2, 2) are two points on the curve. Thus, the log function graph looks as follows.

Logarithmic function properties are helpful to work across complex log functions. All the general arithmetic operations across numbers are transformed into a different set of operations within logarithms. The product of two numbers, when taken within the logarithmic functions is equal to the sum of the logarithmic values of the two functions. Similarly, the operations of division are transformed into the difference of the logarithms of the two numbers. Let us list the important properties of log functions in the below points.

• log ab = log a + log b
• loga/b = log a - log b
• log_ba = (log_c a)/(log_c b) (change of base rule)
• loga^x = x loga
• log_a 1 = 0
• log_a a = 1

The derivation of the logarithmic function gives the slope of the tangent to the curve representing the logarithmic function. The formula for the derivative of the common and natural logarithmic functions are as follows.

• The derivative of ln x is 1/x. i.e., d/dx. ln x = 1/x.
• The derivative of logₐ x is 1/(x ln a). i.e., d/dx (logₐ x) = 1/(x ln a).

The integral formulas of logarithmic functions are as follows:

• The integral of ln x is ∫ ln x dx = x (ln x - 1) + C.
• The integral of log x is ∫ log x dx = x (log x - 1) + C.

Related Topics:

• Exponents
• Exponent Rules
• Properties of Logarithms
• Logs in calculations

How to Solve Logarithmic Functions?

The logarithmic function can be solved using the logarithmic formulas. The product of functions within logarithms is equal (log ab = log a + log b) to the sum of two logarithm functions. The division of two logarithm functions(loga/b = log a - log b) is changed to the difference of logarithm functions. The logarithm functions can also be solved by changing it to exponential form.

How to Graph Logarithmic Functions?

The graph of log function y = log x can be obtained by finding its domain, range, asymptotes, and some points on the curve. To find some points on the curve we can use the following properties:

• log 1 = 0
• log 10 = 1

What are Asymptotes of a Logarithmic Function?

Here are the asymptotes of a logarithmic function f(x) = a log (x - b) + c:

• The vertical asymptote is x = b.
• There is no horizontal asymptote.

How Are Exponential and Logarithmic Functions Related?

The exponential function of the form a^x = N can be transformed into a logarithmic function log_aN = x. Here the exponential functions 2^x = 10 is transformed into logarithmic form as log₂10 = x, to find the value of x. The logarithm counts the numbers of occurrences of the base in repeated multiples.

What is the Difference Between Natural Logarithmic and Common Logarithmic Functions?

The logarithmic functions are broadly classified into two types, based on the base of the logarithms. We have natural logarithms and common logarithms. Natural logarithms are logarithms to the base 'e', and common logarithms are logarithms to the base of 10. Further logarithms can be calculated with reference to any base, but are often calculated for the base of either 'e' or '10'. The natural logarithms are written as log_ex (or) ln x, and the common logarithms are written as log₁₀x (or) log x. To obtain the value of x from natural logarithms, it is equal to the power to which e has to be raised to obtain x.

• e = 2.718
• log_eN = 2.303 ×log₁₀N
• log₁₀N = 0.4343 × log_eN

The value of e = 2.718281828459, but is often written in short as e = 2.718. Also, the above formulas help in the interconversion of natural logarithms and common logarithms.

How to Differentiate Logarithmic Functions?

The differentiation of a logarithmic function results in the inverse of the function. The differentiation of ln x is equal to 1/x. (d/dx .ln x = 1//x). Also, the antiderivative of 1/x gives back the ln function.

What Is the Range of Logarithmic Functions?

The range of a logarithmic function takes all values, which include the positive and negative real number values. Thus the range of the logarithmic function is from negative infinity to positive infinity.

What Is the Domain of Logarithmic Functions?

The logarithms can be calculated for positive whole numbers, fractions, decimals, but cannot be calculated for negative values. Hence the domain of the logarithmic function is the set of all positive real numbers.

What is the Formula for Logarithmic Functions?

The following formulas are helpful to work and solve the log functions.

• log ab = log a + log b
• loga/b = log a - log b
• log_ba = (log a)/(log b)
• loga^x = x loga

What Are Logarithmic Functions Used For?

Logarithmic functions have numerous applications in physics, engineering, astronomy. The numeric measurements in astronomy include huge numbers with decimals and exponents. The huge scientific calculations can be easily simplified and calculated using log functions. The logarithmic functions help in transforming the product and division of numbers into sum and difference of numbers.