Horizontal Asymptote

The horizontal asymptote of a function is a horizontal line to which the graph of the function appears to coincide with but it doesn't actually coincide. The horizontal asymptote is used to determine the end behavior of the function.

Let us learn more about the horizontal asymptote along with rules to find it for different types of functions.

The horizontal asymptote of a function y = f(x) is a line y = k when if either lim ₓ→∞ f(x) = k or lim ₓ→ -∞ f(x) = k. i.e., it is a line which the graph (curve) of the function seems to approach as x→∞ or x→ -∞. It is usually referred to as HA. Here, k is a real number to which the function approaches to when the value of x is extremely large or extremely small. A function may or may not have a horizontal asymptote. But the maximum number of asymptotes that a function can have is 2. i.e., a function can have 0, 1, or 2 asymptotes. Here are some examples of horizontal asymptotes that will give us an idea of how they look like. A horizontal line is usually represented by a dotted horizontal line. When the x-axis itself is the HA, then we usually don't use the dotted line for it.

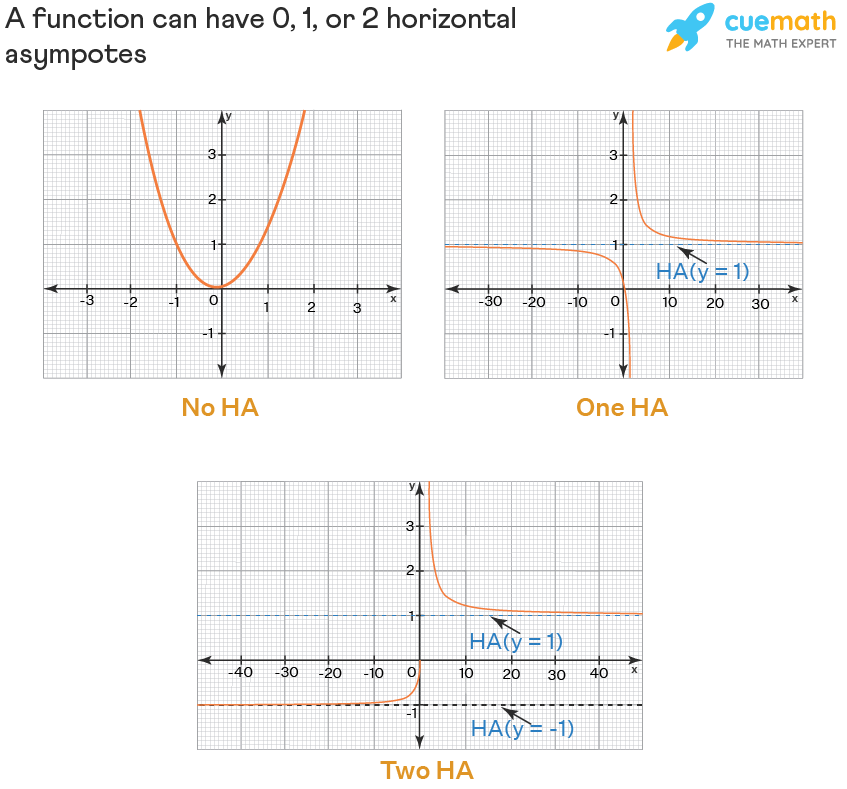
Note that we find the HA while graphing a curve just to represent the value to which the function is approaching. But it is not compulsory to draw it while graphing the curve because it is NOT a part of the curve. Even the graphing calculators do not show a horizontal line for the horizontal asymptote. In other words, a horizontal line is an imaginary line.

Yes, a horizontal asymptote y = k of a function y = f(x) can cross the curve (graph). i.e., there may exist a value of x such that f(x) = k. Note that this is NOT the case with any vertical asymptote as a vertical asymptote never intersects the curve. Here is an example where the horizontal asymptote (HA) is intersecting the curve.

Here, the curve has a horizontal asymptote as x-axis (whose equation is y = 0) and it crosses the curve at (0, 0). Try solving the equation x/(x²+1) = 0 and we will get x = 0.

Here are the steps to find the horizontal asymptote of any type of function y = f(x).

• Step 1: Find lim ₓ→∞ f(x). i.e., apply the limit for the function as x→∞.
• Step 2: Find lim ₓ→ -∞ f(x). i.e., apply the limit for the function as x→ -∞.
• Step 3: If either (or both) of the above limits are real numbers then represent the horizontal asymptote as y = k where k represents the value of the limit.

If either (or both) of the above cases give ∞ or -∞ as the answer then just ignore them and they are NOT the horizontal asymptotes. Sometimes, each of the limits may give the same value and in that case (as in the following example), we have only one HA. To know how to evaluate the limits click here.

Finding Horizontal Asymptote From Graph

In all the above graphs, we can see a common thing. A horizontal asymptote is a parallel line to which a part of the curve is parallel and very close. But note that a HA should never touch any part of the curve (but it may cross the curve).

Example: Find the horizontal asymptote of the function f(x) = 2x / (x - 3).

Solution:

lim ₓ→∞ f(x) = lim ₓ→∞ 2x / (x - 3)
= lim ₓ→∞ 2x / [x (1 - 3/x) ]
= lim ₓ→∞ 2 / (1 - 3/x)
= 2 / (1 - 0)
= 2

So y = 2 is the HA of the function. Now we will find the other limit.

lim ₓ→-∞ f(x) = lim ₓ→-∞ 2x / (x - 3)
= lim ₓ→-∞ 2x / [x (1 - 3/x) ]
= lim ₓ→-∞ 2 / (1 - 3/x)
= 2 / (1 + 0)
= 2

Again, we have got a 2 which gives the same HA to be y = 2.

Thus, the function has only one horizontal asymptote which is y = 2. Here is the graphical verification.

In fact, we use the horizontal asymptote to find the range of a rational function. We just use the fact that the HA is NOT a part of the function's graph. From the above graph, the range of f(x) is {y ∈ R | y ≠ 2}.

But do we need to apply the limits always to find the HA? Isn't any easy method available? Here are some tricks/shortcuts to find the horizontal asymptotes of some specific types of functions.

A rational function can have a maximum of 1 horizontal asymptote. Though we can apply the limits to find the HAs, the other easier way to find the horizontal asymptotes of rational functions is to apply the following tricks:

• If the degree of the numerator > degree of the denominator, then the function has no HA.
• If the degree of the numerator < degree of the denominator, then the function has one HA which is y = 0.
• If the degree of the numerator = degree of the denominator, then the function has one HA which is y = the ratio of the leading coefficients of numerator and denominator.

In the above example from the previous section (where f(x) = 2x / (x - 3) ), the degree of numerator = the degree of the denominator ( = 1). So the HA of f(x) is y = 2/1 = 2. Note that we had got the same answer even when we applied the limits. Here are a few more examples.

• y = (x²+3) / (2x) has no HA.
• HA of y = (2x) / (x² + 3) is y = 0.
• HA of y = (2x²) / (x² + 3) is y = 2.

An exponential function always has exactly one horizontal asymptote. The parent exponential function is of the form f(x) = b^x, but when transformations take place, it can be of the form f(x) = ab^kx + c. Here 'c' represents the vertical transoformation of the parent exponential function and this itself is the horizontal asymptote. To conclude:

• HA of f(x) = b^x is y = 0.
• HA of f(x) = ab^kx + c is y = c.

Using the above hint, the horizontal asymptote of the exponential function f(x) = 4^x + 2 is y = 2 (Technically, y = lim ₓ→ -∞ 4^x + 2 = 0 + 2 = 2).

Here are some examples.

• HA of f(x) = 2^x - 3 is y = -3.
• HA of f(x) = 3^-x + 5 is y = 5.
• HA of f(x) = 0.5^2x - (2/3) is y = -2/3.

Let us summarize all the horizontal asymptote rules that we have seen so far.

• To find the horizontal asymptote of a rational function, find the degrees of the numerator (n) and degree of the denominator (d).
  If n < d, then HA is y = 0.
  If n > d, then there is no HA.
  If n = d, then HA is y = ratio of leading coefficients.
• The horizontal asymptote of an exponential function of the form f(x) = ab^kx + c is y = c.
• A polynomial function (like f(x) = x+3, f(x) = x²-2x+3, etc) cannot have any horizontal asymptote as the limits of these functions as x tends to ∞ or -∞ do not give real numbers.
• To find the horizontal asymptote of any miscellaneous functions other than these, we just apply the common procedure of applying limits as x→∞ and x→ -∞.

Important Notes on Horizontal Asymptote:

• A function doesn't necessarily have a horizontal asymptote.
• The maximum number of asymptotes a function can have is 2.
• A function has two horizontal asymptotes when there is a square root function. For example: f(x) = \(\frac{x+1}{\sqrt{x^{2}-1}}\).
• No polynomial function has a horizontal asymptote. i.e., linear functions, quadratic functions, cubic functions, etc have no HA.
• No basic trigonometric function has a horizontal asymptote.
• No basic logarithmic function has a horizontal asymptote.

☛ Related Topics:

• Horizontal Asymptote Calculator
• Graphing Calculator
• Graphing Functions Calculator

What is Horizontal Asymptote of a Function?

The horizontal asymptote (HA) of a function y = f(x) is the limit of the function f(x) as x→∞ or x→ -∞. A function can have a maximum of 2 HAs.

What are Horizontal Asymptote Rules?

The general rule to find the horizontal asymptote (HA) of y = f(x) is usually given by y = lim ₓ→∞ f(x) and/or y = lim ₓ→ -∞. But here are some tricks that may be helpful in finding the HA of some specific functions:

• The HA of a rational function
  is y = 0 when its numerator's degree is less than the denominator's degree
  does not exist when the numerator's degree is greater than the denominator's degree
  is y = k when both degrees are equal and k = ratio of leading coefficients.
• The HA of an exponential function f(x) = a^x + k is y = k.

What is the Difference Between Vertical and Horizontal Asymptotes?

Asymptotes are lines to which the function seems to be coinciding but actually doesn't coincide. A horizontal asymptote is a horizontal line and is of the form y = k. A vertical asymptote is a vertical line and is of the form x = k.

How to Calculate Horizontal Asymptote?

To find horizontal asymptotes of a function y = f(x), we use the formulas y = lim ₓ→∞ f(x) and y = lim ₓ→ -∞. If any of these limits results in a non-real number, then just ignore that limit.

How to Find Horizontal Asymptote of a Rational Function?

The degree of the numerator (n) and the degree of the denominator (d) are very helpful in finding the HA of a rational function y = f(x).

• if n = d, then HA is, y = ratio of leading coefficients.
• if n > d, then f(x) has no HA.
• if n < d, then HA is y = 0.

How to Find Horizontal Asymptote of an Exponential Function?

The basic exponential function is of the form y = a^x. If some vertical transformation happens, then the function is of the form y = a^x + k. Its HA is just y = k.

How to Find the Range of a Function Using Horizontal Asymptote?

Horizontal asymptote is used to determine the range of a function just in case of a rational function. For example, the HA of f(x) = (2x) / (x²+1) is y = 0 and its range is {y ∈ R | y ≠ 0}.