Domain and Range
Functions in mathematics can be compared to the operations of a vending (soda) machine. When you put in a certain amount of money, you can select different types of sodas. Similarly, for functions, we input different numbers and we get new numbers as the result. Domain and range are the main aspects of functions.
- You can use quarters and one-dollar bills to buy a soda. The machine will not give you any flavor of the soda if pennies are input. Hence, the domain represents the inputs we can have here, that is, quarters and one-dollar bills.
- No matter what amount you pay, you won't get a cheeseburger from a soda machine. Thus, the range is the possible outputs we can have here, that is, the flavors of soda in the machine.
Let us learn to find the domain and range of a function, and also graph them.
What is Domain and Range?
The domain and range of a relation are the sets of all the x-coordinates and all the y-coordinates of ordered pairs respectively. For example, if the relation is, R = {(1, 2), (2, 2), (3, 3), (4, 3)}, then:
- Domain = the set of all x-coordinates = {1, 2, 3, 4}
- Range = the set of all y-coordinates = {2, 3}
We can visualize this here:
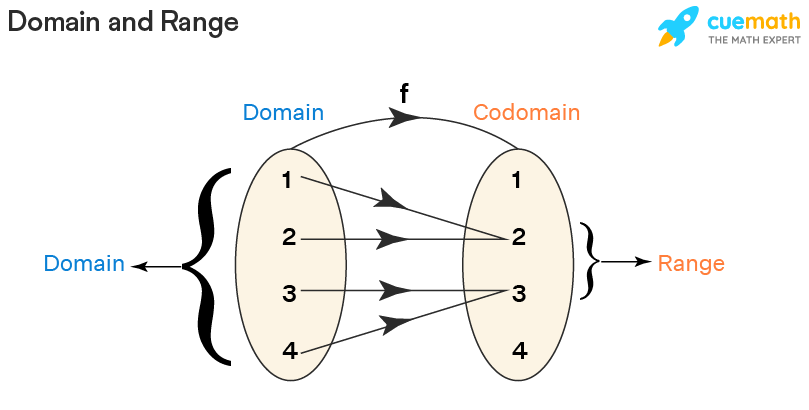
The concept of domain and range is further implemented for functions as well.
Domain and Range of a Function
The domain and range of a function are the components of a function. The domain is the set of all the input values of a function and the range is the possible output given by the function. Domain→ Function →Range. If there exists a function f: A →B such that every element of set A is mapped to elements in set B, then A is the domain and B is the co-domain. The image of an element 'a' under a relation R is given by 'b', where (a,b) ∈ R. The range of the function is the set of images. The domain and range of a function are denoted in general as follows: Domain(f) = {x ∈ R : Condition} and range(f)={f(x) : x ∈ domain(f)}
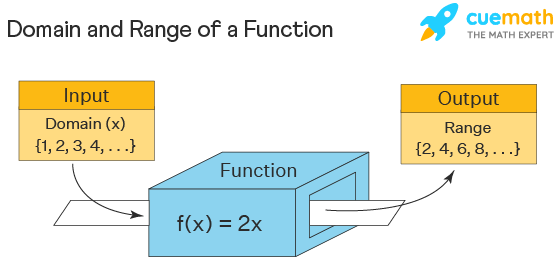
The domain and range of this function f(x) = 2x is given as domain D = {x ∈ N} , range R = {y ∈ N: y = 2x}
Domain of a Function
A domain of a function refers to "all the values" that can go into a function without resulting in undefined values. i.e., The domain in math is the set of all possible inputs for the function. Consider the above box as a function f(x) = 2x . Inputting the values x = {1,2,3,4,...}, the domain is simply the set of natural numbers. But in general (if the domain is not specified as natural numbers), f(x) = 2x is defined for all real values of x and hence its domain is the set of all real numbers which is denoted by (-∞, ∞). Here are the general formulas used to find the domain of different types of functions. Here, R is the set of all real numbers.
Rules of Finding Domain of a Function
- Domain of any polynomial (linear, quadratic, cubic, etc) function is ℝ (all real numbers).
- Domain of a square root function √x is x ≥ 0.
- Domain of an exponential function is ℝ.
- Domain of logarithmic function is x>0.
- To find the domain of a rational function y = f(x), set the denominator ≠ 0.
How to Find Domain of a Function?
To find the domain of a function, we simply apply one of the above-mentioned rules of finding domain depending on the type of the function. Here are some examples:
Example 1: To find the domain of a function f(x) = √(x + 3), we apply the rule 2 mentioned above. Then we get: x + 2 ≥ 0. Solving this inequality, we get x ≥ -2. Thus, the domain of f(x) is [-2, ∞).
Example 2: To calculate the domain of a function g(x) = (2x + 1) / (x - 2), we apply the rule 5 mentioned above. Then we get x - 2 ≠ 0. Solving this, we get x ≠ 2. Thus, its domain is the set of all real numbers except 2 which in interval notation can be written as (-∞, 2) ∪ (2, ∞).
Range of a Function
The range of a function is the set of all its outputs. Example: Let us consider the function f: A→ B, where f(x) = 2x and each of A and B = {set of natural numbers}. Here we say A is the domain and B is the co-domain. Then the output of this function becomes the range. The range = {set of even natural numbers}. The elements of the domain are called pre-images and the elements of the co-domain which are mapped are called the images. Here, the range of the function f is the set of all images of the elements of the domain (or) the set of all the outputs of the function.
Rules of Finding Range of a Function
The best way to determine the range of a function is by graphing it and looking at the y-value that the graph covers. But here are the general rules used to find the range of some popular functions. Note that ℝ is the set of all real numbers here.
- Range of a linear function is ℝ.
- Range of a quadratic function y = a(x - h)2 + k is:
y ≥ k, if a > 0 and
y ≤ k, if a < 0 - Range of a square root function is y ≥ 0.
- Range of an exponential function is y > 0.
- Range of logarithmic function is ℝ.
- To find the range of a rational function y = f(x), solve it for x and set the denominator ≠ 0.
How to Find Range of a Function?
If a function is present in one of the functions mentioned in the above rules, we can straight away apply the rules and find its range. Otherwise, we can graph it and look at the y-values the graph covers to calculate range. Here are some examples:
Example 1: To calculate the range of the function f(x) = 2 (x - 3)2 - 5, apply rule 1 mentioned above. Then its range is y ≥ -5 (or) [-5, ∞).
Example 2: To find the range of a function g(x) = ln (2x - 3) + 4, we apply the rule 4. Then we get its range to be the set of all real numbers (ℝ).
How To Calculate Domain And Range?
Suppose X = {1, 2, 3, 4, 5} and Y = {1, 2, 3, 4, 5, 6}. Consider the function f: X → Y, where R = {(x,y) : y = x+1}.
- Domain = the input values. Thus Domain = X = {1, 2, 3, 4, 5}
- Range = the output values of the function = {1 + 1, 2 + 1, 3 + 1, 4 + 1, 5 + 1} = {2, 3, 4, 5, 6}
Note that Y is the codomain here but NOT range.
Let's understand the domain and range of some special functions taking different types of functions into consideration.
Domain and Range of Exponential Functions
The function y = ax, a ≥ 0 is defined for all real numbers. Hence, the domain of the exponential function is the entire real line. The exponential function always results in a positive value. Thus, the range of the exponential function is of the form y= ax is {y ∈ ℝ: y > 0}. Therefore, Domain = ℝ, Range = (0, ∞)
Example: Look at the graph of this function f: 2x
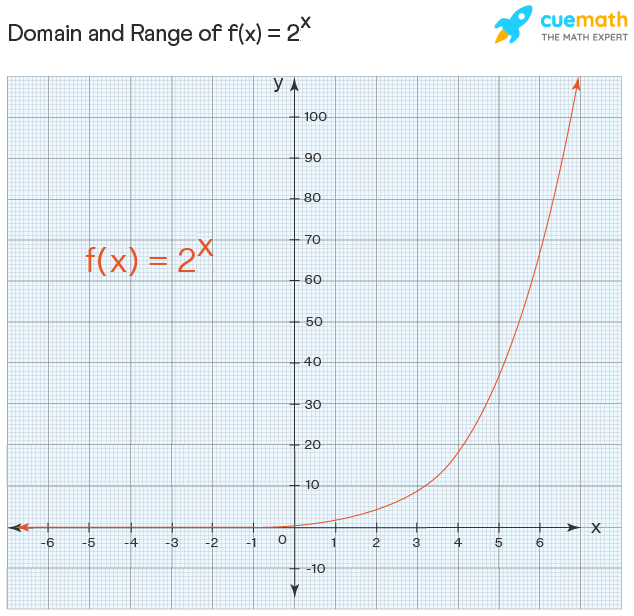
Observe that the value of the function is closer to 0 as x tends to ∞ but it will never attain the value 0. The domain and range of exponential functions are given as follows:
- Domain: The domain of the function is the set ℝ.
- Range: The exponential function always results in positive real values.
Domain and Range of Trigonometric Functions
Look at the graph of the sine function and cosine function. Notice that the value of the functions oscillates between -1 and 1 and it is defined for all real numbers.
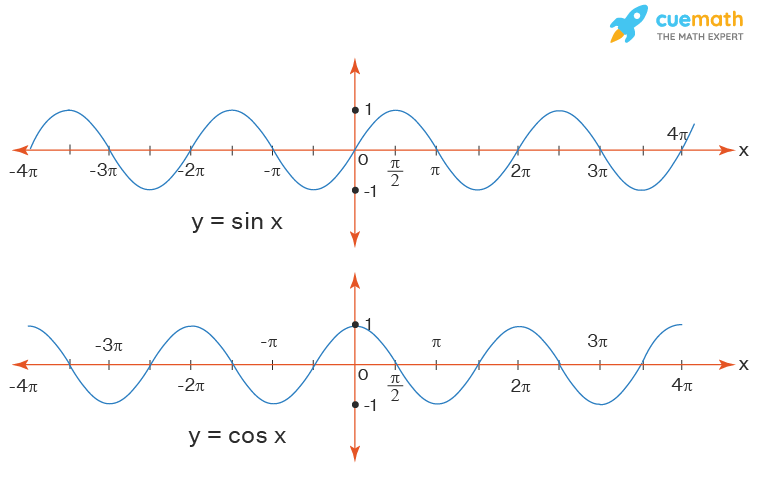
Thus, for each of the sine and cosine functions:
- Domain: The domain of the functions is the set ℝ (or) (-∞, + ∞).
- Range: The range of the functions is [-1, 1]
The domain and range of all trigonometric functions are shown below:
| Trigonometric Functions | Domain | Range |
|---|---|---|
| sin θ | (-∞, + ∞) | [-1, +1] |
| cos θ | (-∞ +∞) | [-1, +1] |
| tan θ | ℝ - (2n + 1)π/2 | (-∞, +∞) |
| cot θ | ℝ - nπ | (-∞, +∞) |
| sec θ | ℝ - (2n + 1)π/2 | (-∞, -1] U [+1, +∞) |
| cosec θ | ℝ - nπ | (-∞, -1] U [+1, +∞) |
Domain and Range of an Absolute Value Function
The function y = |ax + b| is defined for all real numbers. So, the domain of the absolute value function is the set of all real numbers. The absolute value of a number always results in a non-negative value. Thus, the range of an absolute value function of the form y= |ax+b| is {y ∈ ℝ | y ≥ 0}. The domain and range of an absolute value function are given as follows
- Domain = ℝ
- Range = [0, ∞)
Example: Find the domain and range of the function f(x) = |6 - x|.
- Domain: The domain of the function is the set ℝ.
- Range: Its range is [0, ∞)
Domain and Range of a Square Root Function
A square root function is of the form f(x) = √(ax+b). We know that the square root of a negative number is not defined. So the function y= √(ax+b) is defined only when ax + b ≥ 0. When we solve this for x, we get x ≥ -b/a.
So, the domain of the square root function is the set of all real numbers greater than or equal to -b/a. We know that the square root of something always results in a non-negative value. Thus, the range of a square root function is the set of all non-negative real numbers. Hence, the domain and range of a square root function are given as: Domain = [-b/a,∞), Range = [0,∞)
Example: Calculate the domain and range of the function h(x) = 2- √(-3x+2).
Domain: A square root function is defined only when the value inside it is a non-negative number. So for a domain,
-3x+2 ≥ 0
-3x ≥ -2
x ≤ 2/3
Range: We already know that the square root function results in a non-negative value always.
√(-3x+2) ≥ 0
Multiply -1 on both sides
-√(-3x+2) ≤ 0
Adding 2 on both sides
2-√(-3x+2) ≤ 2
y≤ 2
Thus, the domain of h(x) = (-∞, 2/3] and range of h(x) = (-∞, 2].
Domain and Range From Graph
It is very easy to find the domain and range of a graph. The set of values of x covered by the graph gives the domain and the set of values of y covered by the graph gives the range. But keep a note of the following things while writing the domain and range from a graph.
- See whether the graph passes the vertical line test. Otherwise, it is not a function and we do not usually define domain and range for such curves.
- If there is any hole on the graph, then its coordinates shouldn't be in the domain and range.
- If there is a vertical asymptote, then the corresponding value of x shouldn't be there in the domain.
- If there is a horizontal asymptote, then the corresponding value of x shouldn't be there in the range.
- If the graph is broken into pieces, then we get multiple sets/intervals in the domain and range and we club all such sets/intervals by "union" symbol (∪).
- If there is an arrow at the end of a curve, then it means that the curve is supposed to be extended infinitely in that particular direction.
Example 1:
Here is an example of a graph and we will find the domain and range of the graph.
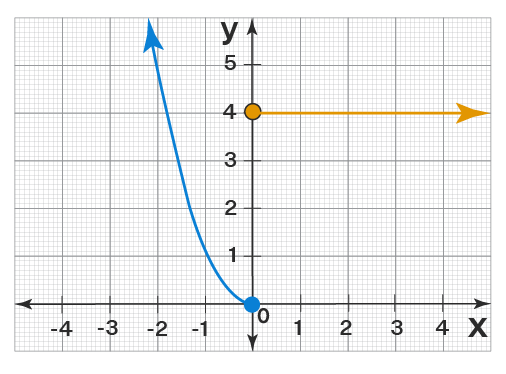
In the above graph:
- All the x-values from -∞ to ∞ are covered by the graph (because of arrows, the two curves extend infinitely in the given directions). Hence, the domain = (-∞, ∞).
- All the y-values greater than or equal than or equal to 0 are covered by the graph (see there is no part of the curve that is below the y-axis). Hence, the range = [0, ∞).
Example 2: Using the same process mentioned above, the domain of the graph below is [-5, ∞) and its range from graph is (-∞, 5].
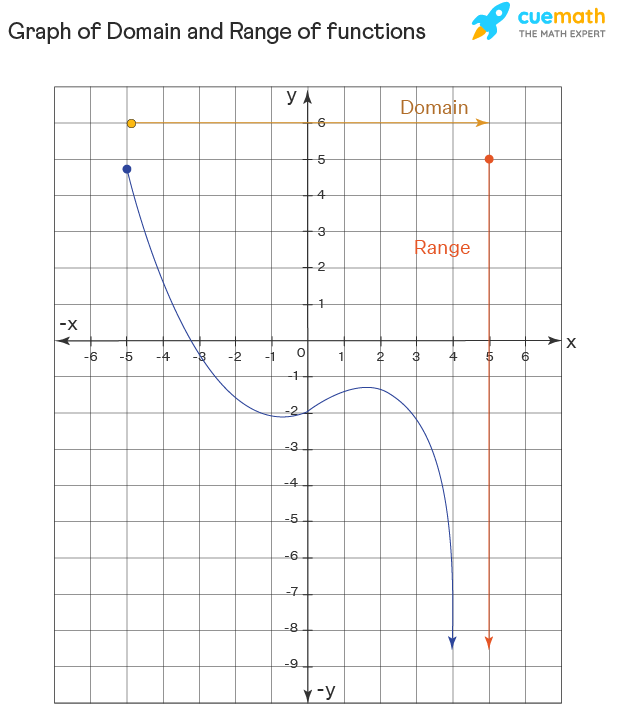
Important Notes on Domain and Range:
- The domain and range of a function is the set of all possible inputs and outputs of a function respectively.
- To find the domain of a function f(x), think for what values of x it is defined.
- To calculate the range of a function f(x), think of what y values it will produce. The most easiest way to find the range of a function is to graph it.
☛ Related Topics:
Examples on Domain and Range
-
Example 1. Find the domain and range of the real function f defined by f(x) = √(x - 1)
Solution:
Method 1:
Given the function is real. Thus the domain and range of the function are also real.
x √(x-1) Real Number(Yes/No) 2 √(2-1) = 1 Yes 1 √(1-1) =0 Yes 0 √(0-1) =√-1 No -1 √(-1-1) = √-2 No -2 √(-2-1) = √-3 No The minimum value it could take is 1 and the maximum value is ∞. Thus domain = [1, ∞).
Since f(x) is always non-negative, the minimum value of the range is 0 and it can range up to infinity. Thus range = [0, ∞)
Method 2:
Using the rules of finding domain, the domain of f(x) is obtained by solving x - 1 ≥ 0. Then we get x ≥ 1. Thus, the domain is [1, ∞).
Range of a square root is always the set of all non-negative numbers. Thus, the range is [0, ∞).
Answer: The domain and the range of the function f defined by f(x) = √(x - 1) is domain = [1, ∞) and range = [0, ∞)
-
Example 2: We define a function f: R - {0} → R as f(x)=1/x. Complete the table shown below. Find the domain and range of the function.
x -2 -1.5 -1 -0.5 0.25 0.5 1 1.5 2 Solution:
Let's complete the given table by finding the values of the function at the given values x. Plugging in the values of x in the given function, we find the range of f(x) = 1/x.
x y=1/x -2 0.5 -1.5 -0.67 -1 -1 -0.5 -2 0.25 4 0.5 2 1 1 1.5 0.67 2 0.5 Let's draw the graph of the function to determine the domain and range of the function.
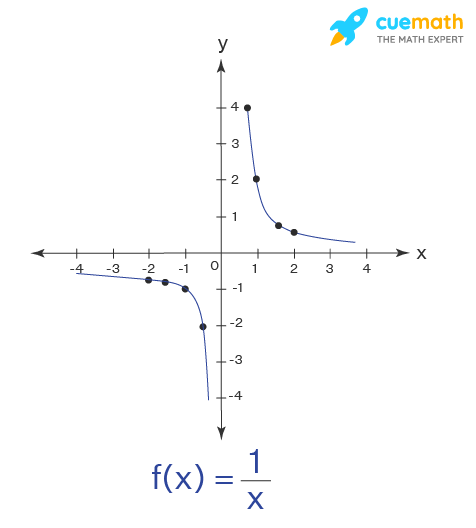
From the graph, we can observe that the domain and range of the function are all real numbers except 0.
Answer: So, the domain and range of f(x) = 1/x is R - {0} (or) (-∞,0) ∪ (0, ∞).
-
Example 3: Find the domain and range of the function y = (x + 1)/(3 - x).
Solution:
A rational function is defined only when its denominator is NOT 0.
Thus, we will set the denominator NOT equal to 0, and then we will solve for x.
3 - x ≠ 0
- x ≠ - 3 ⇒ x ≠ 3
So, the domain is the set of real numbers x except 3, i.e., domain = (-∞, 3) ∪ (3, ∞).
Let's find the range of y = (x + 1)/(3 - x)
Let us solve the given equation for x
(3 - x)y = x + 1
3y - xy = x + 1
3y-1 = x + xy
x(1 + y) = 3y - 1
x = (3y - 1)/(1 + y)
The final equation is a fraction and a fraction is NOT defined when its denominator is zero.
So 1 + y ≠ 0 ⇒ y ≠ -1
Therefore, the range of the given function is the set of all real numbers excluding -1. i.e., the range = (-∞,-1) ∪ (-1, ∞).
Answer: Domain = (-∞, 3) ∪ (3, ∞), Range = (-∞,-1) ∪ (-1, ∞)

FAQs on Domain and Range
What is the Domain and Range of a Function?
The domain and range of a function are the set of all the inputs and outputs a function can give respectively. i.e., for any function y = f(x):
- the domain is the set of all x-values for which f(x) is defined.
- the range is the set of all y-values that the function f(x) produce.
How Do You Write the Domain and Range?
We write the domain and range of a function as the set of all the inputs a function can take and the outputs of the functions respectively. Since these are nothing but sets, we can write them either in roaster form or set builder notation. The domain and range in the interval notation involve open and square brackets.
How to Find Domain and Range of a Graph?
The domain from a graph is the set of all x-values the graph covers and the range of a graph is the set of all y-values that it covers.
What is The Domain and Range of a Constant Function?
Let the constant function be f(x) = k. The domain of a constant function is given by ℝ, that is, the set of real numbers. The range of a constant function is given by the singleton set, {k}. The domain and range of a constant function is given as domain = ℝ and range = {k}, which is a singleton set.
What is the Definition of Domain in Math?
The domain in math is usually defined for relations/functions. The domain of a function is the set of all values that are possible to input into it. For example, for the function f(x) = √x, it is possible to input only non-negative values into it. Thus, its domain is the set of all non-negative real numbers.
How to Find the Domain of a Function which is Rational?
To find the domain of a rational function, we just set the denominator not equal to zero. For example, to find the domain of f(x) = 2/(x-3), we set x-3 ≠ 0, by solving this, we get x≠3. So the domain is the set of all rational numbers except 3. This can be written in the interval notation as (-∞, 3) U (3, ∞).
What are the Rules to Find the Domain of a Function?
Here are some general rules used to find domain of different types of functions:
- f(x) = polynomial, the domain is the set of all real numbers.
- f(x) = 1/x, domain if the set of all real numbers but x≠0.
- f(x) = √x, domain if the set of all real numbers such that x ≥ 0.
- f(x) = ln x, domain is the set of all real numbers such that x > 0.
How to Find Domain and Range of Function?
To find the domain of a function y = f(x), we need to look for set of all possible values of x that does not make the function undefined. The common examples include dividing by 0, taking the square root of negative numbers, etc. To calculate the range of a function, imagine what y-values the function produces. When imagination is not possible, graph the function and take a look at the y-values that the graph covers.
How to Find Range of a Rational Function?
To find the range of a rational function, we just solve the equation for x and set the denominator not equal to zero. For example, to find the range of y=2/(x-3), solve it for x first. Then we get, x-3 = 2/y and from this, x = (2/y) + 3. Then its range is y≠0 (or) in interval notation, (-∞, 0) U (0, ∞).
How to Find Domain and Range of an Equation?
To find the domain and range of an equation y = f(x), determine the values of the independent variable x for which the function is defined. To calculate the range of the function, we simply express the equation as x = g(y) and then find the domain of g(y).
How to Calculate the Domain and Range From the Graph of a Function?
The set of all x-coordinates of all points of the curve would give the domain and the set of all y-coordinates of all points of the curve would give the range. Each of domain and range can be either written as a set or an interval.
What is The Difference Between Domain and Range of a Function?
Domain and Range of a function are the components of a function. The domain of a function is the set of all possible inputs for the function, whereas the range of function is the set of all the outputs a function can give.
What is The Domain and Range of a Relation?
The domain and range of a relation is found as follows. Let R be the relation from a non-empty set A to a non-empty set B. The domain and range of the relation are the set of first elements and the second elements respectively in the ordered pairs in relation R is called the domain.
What is the Domain and Range of Composite Functions?
Let the composite function be h(x) = (f ∘ g)(x). The domain and range of h are determined as follows. The domain of h is either same as f or lies within the domain of f. The range h must lie within the range of g. Let f(x) = x2 and g(x) = x+ 3. We know that g: X →Y and f: Y →Z. Then fog: X →Z. f(g(x)) = (x+3)2. Thus the domain and range are: domain= {All the elements in set X}, range= {all the elements in set Z}
What is the Domain and Range of a Quadratic Function?
The domain and range of a quadratic function y = a(x - h)2 + k determine the nature of the parabola: whether it is upwards or downwards.
- y ≥ k, if the function has a minimum value, that is, when a > 0 (parabola opens up)
- y ≤ k, if the function has a maximum value, that is, when a < 0 (parabola opens down)
How to Find the Range of a Graph?
The y-axis is responsible for range. Thus, to find the range of a graph look at the y-values covered by the graph. The highest and lowest values of the graphs are helpful in writing the range of a graph.
visual curriculum