Ordered Pair
An ordered pair, as its name suggests, is a pair of elements that have specific importance for the order of their placements. Ordered pairs are usually used in coordinate geometry to represent a point on a coordinate plane. Also, they are used to represent elements of a relation.
Let us learn more about ordered pairs along with its definition, meaning, properties, and more.
What is an Ordered Pair?
An ordered pair is a pair formed by two elements that are separated by a comma and written inside the parantheses. For example, (x, y) represents an ordered pair, where 'x' is called the first element and 'y' is called the second element of the ordered pair. These elements have specific names according to what context they are being used and they can be either variables or constants. The order of the elements has a certain importance in an ordered pair. It means (x, y) may not be equal to (y, x) all the time.

(2, 5), (a, b), (0, -5), etc are some examples of ordered pairs.
Ordered Pair in Coordinate Geometry
An ordered pair in coordinate geometry is used to represent the position of a point on the coordinate plane with respect to the origin. A coordinate plane is formed by two perpendicular intersecting lines among which one is horizontal (x-axis) and the other line is vertical (y-axis). The intersecting point of both axes is the origin. Every point on the coordinate plane is represented by an ordered pair (x, y) where the first element x is called the x-coordinate and the second element y is called the y-coordinate. We can see more differences between the elements of the ordered pair used in geometry here.
| First Element of Ordered Pair | Second Element of Ordered Pair |
|---|---|
| It is called x-coordinate. | It is called y-coordinate. |
| Another name for this is "abscissa". | Another name for this is "ordinate". |
| It represents the horizontal distance of the point from the origin. | It represents the vertical distance of the point from the origin. |
| This number is one of the numbers on the x-axis. | This number is one of the numbers on the y-axis. |
| It represents the distance of the point from the y-axis. | It represents the distance of the point from the x-axis. |
| Example: If (2, 4) is a point on the coordinate plane, then 2 is the distance of the point from the y-axis.  |
Example: If (2, 4) is a point on the coordinate plane, then 2 is the distance of the point from the y-axis.  |
Graphing Ordered Pairs
Now, we understood the difference between the x-coordinate and y-coordinate of an ordered pair in coordinate geometry. Let us now see the steps to graph ordered pairs.
- Step 1: Always start from the origin and move horizontally by |x| units to the right if x is positive and to the left if x is negative. Stay there.
- Step 2: Start from where you have stopped in Step 1 and move vertically by |y| units to up if y is positive and to down if y is negative. Stay there.
- Step 3: Place a dot exactly at the point where you have stopped in Step 2 and that dot represents the ordered pair (x, y)
In these steps, |x| and |y| represent the absolute values of x and y respectively.
Example: Graph the ordered pair (4, -3).
Let's start from the origin, move to the right by 4 units (as 4 is positive) and then move down by 3 units (as 3 is negative).

The order of the elements in an ordered pair is important and hence the name "ordered" pair. For example, (4, -3) and (-3, 4) are located at different positions on the plane as shown below.
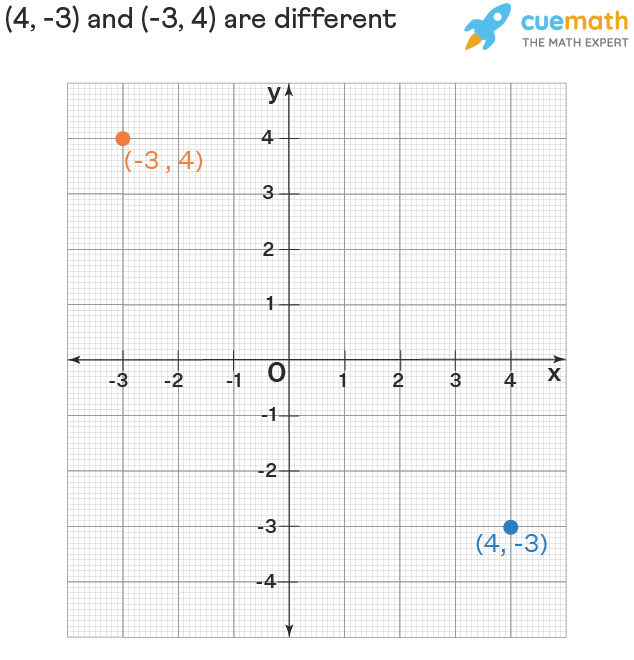
Ordered Pairs in Different Quadrants
We can see in the above figure that the coordinate plane is divided into 4 parts by the x and y axes. Each of these 4 parts is known as a quadrant. The signs of x and y in an ordered pair (x, y) of a point differs depending upon the quadrant and they are shown in the table below.
| Quadrant | Ordered Pair Signs |
|---|---|
| I | x > 0, y > 0 |
| II | x < 0, y > 0 |
| III | x < 0, y < 0 |
| IV | x > 0, y < 0 |
For example, (2, -4) refers to 2 on the x-axis (positive) and -4 on the y-axis (negative). So (2, -4) is a point in quadrant IV.
Ordered Pair in Sets
Till now we have seen that ordered pairs are used in coordinate geometry to locate a point. But they are used in set theory as well in a different context. The set of all possible ordered pairs from a set A to a set B is called the cartesian product. For example, if A = {1, 2, 3} and B = {a, b, c}, then the cartesian product is A x B = {(1, a), (1, b), (1, c), (2, a), (2, b), (2, c), (3, a), (3, b), (3, c)} and it is a set formed by all ordered pairs (x, y) where x is in A and y is in B. Any subset of the cartesian product is called a relation. For example, {(1, a), (1, b), (3, c)} is a relation.
Examples:
- If (2, 4) belongs to a relation "divides", it means that 2 divides 4.
- If (4, 2) belongs to a relation "greater than", it means that 4 is greater than 2.
- If (x, y) belongs to a relation "is a sister of", it means that x is a sister of y.
Equality Property of Ordered Pairs
For any two ordered pairs (x, y) and (a, b) (either in coordinate geometry or in relations), if (x, y) = (a, b) then x = a and y = b. i.e., if two ordered pairs are equal, then their corresponding elements are equal. This is called "equality property of ordered pairs". For example:
- If (x, y) = (2, -3) then x = 2 and y = -3.
- If (x + 1, y - 2) = (-3, 5) then x + 1 = -3 and y - 2 = 5.
Important Notes on Ordered Pairs:
- An ordered pair (x, y) is used to represent the location of a point in coordinate geometry where x is the horizontal distance and y is the vertical distance of the point.
- An ordered pair (x, y) represents an element of a relation R which is denoted by xRy (x "is related to" y).
- If (x, y) = (a, b) then x = a and y = b.
Related Topics:
Ordered Pair Examples
-
Example 1: Plot the point with the ordered pair (-2, 3). State the quadrant in which it lies.
Solution:
To plot the point (-2, 3):
- Move 2 units left from the origin (as -2 is negative)
- Thereby, move 3 units to up (as 3 is positive)
- Place a dot where you have reached.
Then the point on the graph looks like this.

Answer: We have plotted (-2, 3) and it lies in the Quadrant II.
-
Example 2: Find the values of x and y if (2x - 3, 3y + 2) = (5, 8).
Solution:
It is given that (2x - 3, 3y + 2) = (5, 8).
By the equality property of ordered pairs,
2x - 3 = 5 ... (1)
3y + 2 = 8 ... (2)
From (1),
2x = 8 (or) x = 4
From (2),
3y = 6 (or) y = 2
Answer: x = 4 and y = 2.
-
Example 3: Identify the quadrants in which the following ordered pairs lie without plotting them. (a) (2, -3) (b) (-2, -3).
Solution:
In (2, -3), x-coordinate is positive and y-coordinate is negative. So it lies in Quadrant IV.
In (-2, -3), both x and y coordinates are negative. So it lies in Quadrant III.
Answer: (a) lies in IV (b) lies in III.

FAQs on Ordered Pair
What is the Definition of Ordered Pair?
An ordered pair refers to a pair of two numbers (or variables) written inside brackets and are separated by a comma. For example, (1, 2) is an ordered pair. In coordinate geometry, it represents a point and in set theory, it represents an element of a relation/cartesian product.
What is an Ordered Pair in Math?
In math, an ordered pair is a pair of two elements (numbers or variables or combination of both number and variable) that is of the form (x, y) where the order of the elements x and y is important. It means (x, y) may/may not be equal to (y, x).
What is the Process of Graphing Ordered Pairs?
To graph an ordered pair (a, b), calculate their absolute values |a| and |b| first. Then graph it using the following steps:
- Start from (0, 0) and move to left/right by |a| units depending on whether 'a' is negative/positive respectively.
- Start from where you have stopped in the previous step and thereby move up/down by |b| units depending on whether b is positive/negative respectively and stop there.
- Place a dot at the point where you stopped. That is your (a, b).
What are the Applications of Ordered Pair?
The ordered pairs in math are used:
- to represent points on coordinate planes.
- to represent data in statistics.
- to represent an element of a relation/a function.
- to locate a pixel on computer/TV screens.
What is the Equality Property of Ordered Pairs?
The equality property of ordered pairs says that if two ordered pairs are equal then their corresponding elements are equal. i.e., if (x₁, y₁) = (x₂, y₂), then x₁ = x₂ and y₁ = y₂. i.e., the first elements of both pairs are equal and the second elements of both pairs are equal.
Give Examples of Ordered Pairs in Different Contexts.
An ordered pair gives different meanings depending upon different contexts. For example, the ordered pair (10, 20)
- in coordinate geometry represents a point on the coordinate plane that is at a horizontal distance of 10 units and a vertical distance of 20 units from the origin.
- in a relation R that is defined as "is a factor of" represents that 10 is a factor of 20.
- in a table of data with the columns "weeks" and "cars sold" in statistics means that in 10 weeks, 20 cars are sold.
visual curriculum