Piecewise Function
A piecewise function is a function with multiple pieces of curves in its graph. It means it has different definitions depending upon the value of the input. i.e., a piecewise function behaves differently for different inputs.
Let us learn more about piecewise function along with how to graph it, how to evaluate it, and how to find its domain and range.
| 1. | What is Piecewise Function? |
| 2. | Piecewise Function Graph |
| 3. | Domain and Range of Piecewise Function |
| 4. | Evaluating Piecewise Function |
| 5. | Piecewise Continuous Function |
| 6. | FAQs on Piecewise Function |
What is Piecewise Function?
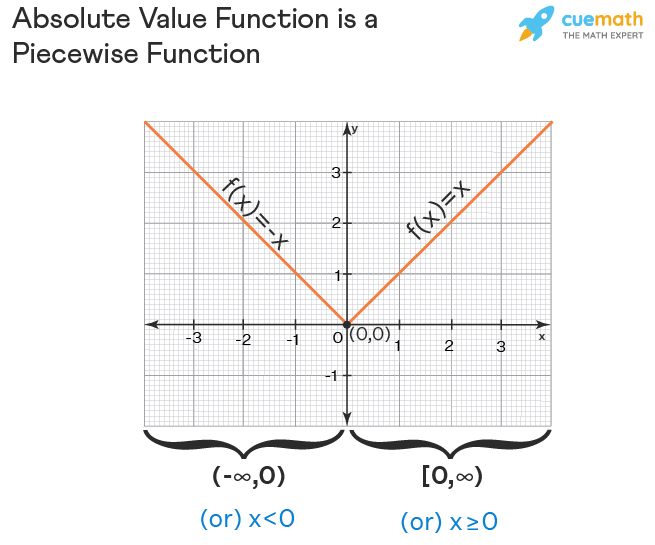
A piecewise function is a function f(x) which has different definitions in different intervals of x. The graph of a piecewise function has different pieces corresponding to each of its definitions. The absolute value function is a very good example of a piecewise function. Let us see why is it called so. We know that an absolute value function is f(x) = |x| and it is defined as: \(f(x)=\left\{\begin{array}{ll}
x, & \text { if } x \geq 0 \\
-x, & \text { if } x < 0
\end{array}\right.\). We should read this piecewise function as
- f(x) is equal to x when x is greater than or equal to 0 and
- f(x) is equal to -x when x is lesser than 0
Then the graph of absolute value function of f(x) has two pieces one corresponds to x (when x is in the interval [0, ∞) ) and the other piece corresponds to -x (when x is in the interval (-∞, 0)). Its graph looks as follows:
Piecewise Function Graph
We already know that the graph of a piecewise function has multiple pieces where each piece corresponds to its definition over an interval. Here are the steps to graph a piecewise function.
- First, understand what each definition of the function represents. For example, f(x) = ax + b represents a linear function (which gives a line), f(x) = ax2 + bx + c represents a quadratic function (which gives a parabola), etc, so that we will have an idea of what shape the piece of the function would result in.
- Write the intervals that are shown in the definition of the function along with their definitions.
- Make a table with two columns labeled x and y corresponding to each interval. Include the endpoints of the interval without fail. If the endpoint is excluded from the interval then note that we get an open dot corresponding to that point in the graph.
- In each table, take more numbers (random numbers) in the column of x that lie in the corresponding interval to get the perfect shape of the graph. If the piece is a straight line, then 2 values for x are sufficient. Take 3 or more numbers for x if the piece is NOT a straight line.
- Substitute each x value from every table in the corresponding definition of the function to get the respective y values.
- Now, just plot all the points from the table (taking care of the open dots) in a graph sheet and join them by curves.
Here is an example to understand these steps.
Example: Graph the piecewise defined function \(f(x)=\left\{\begin{array}{ll}
-2^{x}, & x<-2 \\
-|x|, & -2 \leq x \leq 0 \\
2-x^{2}, & x>0
\end{array}\right.\).
Solution:
f(x) has 3 definitions:
- -2x when x is less than -2 and this is an exponential function.
- -|x| when -2 is less than or equal to x less than or equal to 0 and this is an absolute value function.
- 2-x2 when x is greater than 0 and this is a quadratic function.
Let us write the intervals and their corresponding definitions. Also, let us frame tables that include the endpoints of the intervals and also several other random numbers from each interval. We will calculate the value of y in each case using the corresponding definition.

Now, let us plot all these points on the graph keeping in mind the general shapes of the respective functions. Note that we have to put open dots at (-2, -0.25) (first table) and (0, 2) (last table) as their corresponding x-coordinates are excluded from the interval. Also, extend the graph in the respective intervals beyond the points shown in the tables where required.
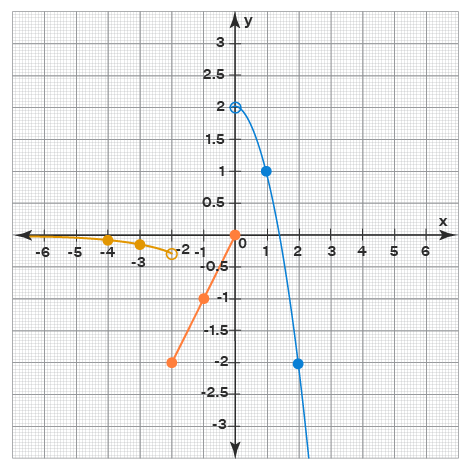
Note that the left most (light orange colored) curve is extended to the left side as it corresponds to the interval x < -2. Also, the right-most (blue-colored) curve is extended in the interval x > 0. The middle (dark orange colored) curve is NOT extended on either side as it belongs to the interval -2 ≤ x ≤ 0.
Domain and Range of Piecewise Function
To find the domain of a piecewise function, we can just look at the given function's definition. Take the union of all intervals with x and that will give us the domain. In the above example, the domain of f(x) is, {x | x < -2} U {x | -2 ≤ x ≤ 0} U {x | x > 0}. The union of all these sets is just the set of all real numbers. So the domain of f(x) (in the above example) is R.
To find the range of a piecewise function, the easiest way is to graph it and look at the y-axis. See what y-values are covered by the graph. In the above example, all y-values less than 2 (exclude 2 as there is an open dot at (0, 2)) are covered by the graph. So its range is {y | y < 2} (or) (-∞, 2).
Similarly, we can find the domain and range of any piecewise function just by graphing it.
Evaluating Piecewise Function
To evaluate a piecewise function at any given input,
- first, see which of the given intervals (or inequalities) the given input belongs to.
- Then just substitute the given input in the function definition corresponding to that particular interval.
Here is an example to understand the steps.
Example: Evaluate f(4) if \(f(x)=\left\{\begin{array}{l} -x^2, \text { if } x<0 \\-2 \sqrt{x}, \text { if } x>0 \\ 5, \text { if } x=0\end{array}\right.\).
Solution:
We have to find f(4). Here x = 4 and it satisfies the condition x > 0. So the corresponding function is f(x) = -2√x.
Substitute x = 4 in this definition:
f(4) = -2 √4 = -2 (2) = -4.
Therefore, f(4) = -4.
Piecewise Continuous Function
A piecewise continuous function, as its name suggests, is a piecewise function that is continuous, It means, its graph has different pieces in it but still we will be able to draw the graph without lifting the pencil. Here is an example of a piecewise continuous function.
\(f(x)=\left\{\begin{array}{l} x-1, \text { if } x<-2 \\-3, \text { if } x\geq -2\end{array}\right.\).
Its graph is shown below.

Important Notes on Piecewise Functions
- To evaluate a piecewise function at an input, see which interval it belongs to and substitute it in the respective definition of the function.
- While graphing a piecewise function, use open dots at the points whose x-coordinates do not belong to the corresponding intervals. An open dot at a point means that a particular point is NOT a part of the function.
- To find the domain of a piecewise function, just take the union of all intervals given in the definition of the function.
- To find the range of a piecewise function, just graph it and look for the y-values that are covered by the graph.
☛ Related Topics:
Piecewise Function Examples
-
Example 1: Graph the piecewise function \(f(x)=\left\{\begin{array}{ll}
-2 x, & -1 \leq x<0 \\
x^{2}, & 0 \leq x<2
\end{array}\right.\).Solution:
Let us make tables for each of the given intervals using their respective definitions of the function.

Let us just plot them and join them by curves. We do not need to extend any of the curves here as none of the intervals have the limits as ∞ or -∞.
Note that we have not an open dot at (0, 0) in the first table because its a closed point in the second table and both curves meet there.

Note that there was supposed to be an open dot at (0, 0) from the first table. But it has become a part of the function from the second table and hence there shouldn't be open dot at (0, 0) and the function is continuous at (0, 0).
Answer: The given function is graphed.
-
Example 2: Find the domain and range of the piecewise function that is given in Example 1.
Solution:
The given intervals are -1 ≤ x < 0 and 0 ≤ x < 2. So their union is -1 ≤ x < 2. This is the domain. The domain in interval notation is [-1, 2).
For the range, look at the graph in Example 1 and see what y-values are being covered. All y-values less than 4 and greater than or equal to 0 are covered. Hence range is [0, 4)
Answer: Domain is [-1, 2) and range is [0, 4).
-
Example 3: Consider the following function: \(f(x)=\left\{\begin{aligned}
1, & x \in \mathbb{Q} \\
-1, & x \notin \mathbb{Q}
\end{aligned}\right.\). Compute the values of (i) f(1), (ii) f(√2), and (iii) f(π).Solution:
The given function is piecewise and so we have to look for the intervals in which each of the given inputs lie in.
(i) Since 1 is a rational number (i.e., 1 ∈ Q), f(1) = 1.
(ii) Since √2 is an irrational number (i.e., √2 ∉ Q), f(√2) = -1.
(ii) Since π is an irrational number (i.e., π ∉ Q), f(π) = -1.
Answer: (i) f(1) = 1; (ii) f(√2) = -1; (iii) f(π) = -1.

FAQs on Piecewise Function
What is Piecewise Defined Function?
A piecewise defined function (which is also known as a piecewise function) is a function that has different definitions over different intervals of inputs. An example of a piecewise function is \(f(x)=\left\{\begin{array}{ll}
2x-3 & \text { if } x<-2 \\
-|x|+5 & \text { if }-2 \leq x<3 \\
x^2-2 & \text { if } x \geq 3
\end{array}\right.\).
How to Graph Piecewise Functions?
To draw a piecewise function graph:
- Make a table (with two columns x and y) for each definition of the function in the respective intervals.
- Include endpoints (in the column of x) of each interval in the respective table along with several other random numbers from the interval.
- Substitute every x value in the corresponding expression of f(x) that gives value in the y-column.
- Plot all the points (put open dots for the x-values that are excluded) and join them by curves.
- If the left/right endpoint is ∞ or -∞ then extend the curve on that side accordingly.
How to Solve Piecewise Functions?
To solve the value of a piecewise function at a specific input:
- Just see which of the given intervals that input lies in.
- Take the corresponding function.
- Substitute the given input in the function from the last step.
Give an Example of a Piecewise Linear Function.
A piecewise linear function is a piecewise function in which all pieces correspond to straight lines. For example, the absolute value function, step function (floor function or greatest integer function), ceiling function, etc are examples of piecewise linear functions.
What is a Piecewise Continuous Function?
A piecewise continuous function is a function that is piecewise and continuous. Its graph has more than one part and yet it is possible to graph it without lifting the pencil.
How to Find Domain and Range of a Piecewise Function?
The domain of a piecewise function is the union of all intervals that are given in its definition. The range is the set of all y-values that its graph covers. So to find the range of a piecewise function, graph it first.
visual curriculum