Greatest Integer Function
The greatest integer function is also known as the step function. It rounds up the number to the nearest integer less than or equal to the given number. The graph of the greatest integer function is a step curve which we will explore in the following sections. The domain of the greatest integer function is ℝ and its range is ℤ.
Therefore the greatest integer function is simply rounding off the given number to the greatest integer that is less than or equal to the given number. Here we shall learn more about the greatest integer function, its graph, and its properties.
What is Greatest Integer Function?
Greatest integer function is a function that gives the greatest integer less than or equal to a given number. The greatest integer less than or equal to a number x is represented as ⌊x⌋. We will round off the given number to the nearest integer that is less than or equal to the number itself. Mathematically, the greatest integer function ⌊x⌋ can be defined as follows:
- ⌊x⌋ = n, where n ≤ x < n + 1 and 'n' is an integer.
Here, 'x' can be any real number but 'n' is always an integer. i.e., irrespective of what number is being set as input to the function, the output is always an integer.
For example, ⌊3.02⌋ = 3, as 3 ≤ 3.02 < 4.
☛Note: The greatest integer function results in the same number if the input is an integer. Examples: ⌊3⌋ = 3, ⌊-4⌋ = -4, etc.
Clearly, the input variable x can take on any real value. However, the output will always be an integer. Also, all integers will occur in the output set.
Domain and Range of Greatest Integer Function
The greatest integer function has the domain of the function as the set of all real numbers (ℝ), while its range is the set of all integers (ℤ). Let us understand the domain and range of the function by observing the following examples of the greatest integer function in the following table:
| Values of x | f(x)=⌊x⌋ |
|---|---|
| 3.1 | f(3.1) = ⌊3.1⌋ = 3 |
| 2.999 | f(2.999) = ⌊2.999⌋ = 2 |
| −2.7 | f(−2.7) = ⌊−2.7⌋ = −3 |
| 4 | f(4) = ⌊4⌋ = 4 |
| −7 | f(−7) = ⌊−7⌋ = −7 |
Here, the values of x can be any real number, and hence the domain of the greatest integer function is ℝ. But observe that all the values of f(x) (y-values) are integers and hence the range is ℤ.
Greatest Integer Function Graph
The greatest integer function graph is known as the step curve because of the step structure of the curve. Let us plot the greatest integer function graph. First, consider f(x) = ⌊x⌋, if x is an integer, then the value of f will be x itself. If x is a non-integer, then the value of x will be the integer just before x (on the left side of x).
For example,
- For all numbers lying in the interval [0, 1), the value of f will be 0.
- For the entire interval [1, 2), f will give the value 1.
- For the interval [−1, 0), f will be the value −1 and so on.
So for an integer n, all the numbers that lie in the interval [n, n+1) will have the value of the greatest integer function as n. The function has a constant value between any two integers. As soon as the next integer comes, the function value jumps by one unit. This means that the value of f at x = 1 is 1 (and not 0) hence there will be a hollow dot at (1, 0) and a solid dot at (1, 1) where a hollow dot means not including the point and solid dot represents including the point. These observations lead us to the following graph.
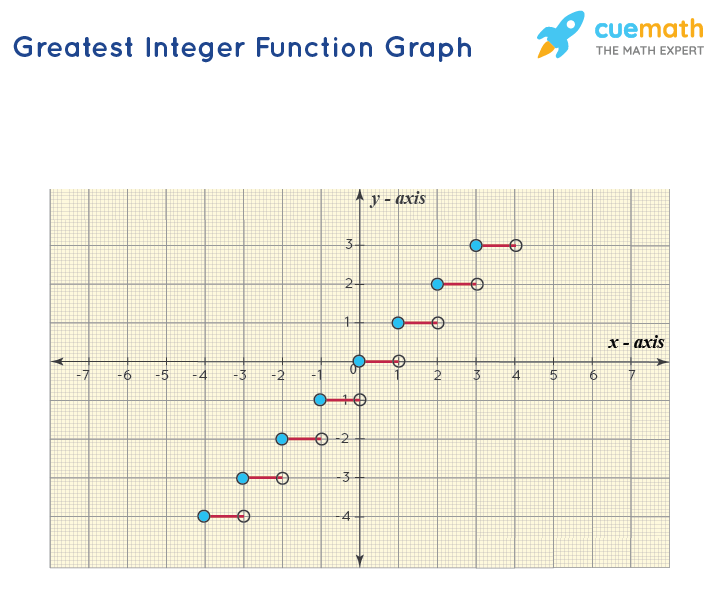
From the graph above we can clearly see that inputs of the function can be any real number but the output will always be an integer. Thus, the domain of this function is real numbers (ℝ), while its range will be integers (ℤ).
Greatest Integer Function Properties
The greatest integer function has numerous properties. Some of the important properties are listed below.
- ⌊x+n⌋ = ⌊x⌋+n, where, \(n \in \mathbb{Z}\)
- ⌊−x⌋ = \(\begin{cases} & {-\left\lfloor x\right\rfloor}, & \text{if } x \in \mathbb{Z} \\ &{-\left\lfloor x \right\rfloor-1}, & \text{if } x \notin \mathbb{Z} \\ \end{cases}\)
- If ⌊f(x)⌋ ≥ L, then f(x) ≥ L
- If ⌊f(x)⌋ ≤ L, then f(x) < L + 1.
Greatest Integer Function and Smallest Integer Function
Let us understand the smallest integer function along with seeing how it is different from the greatest integer function.
| Greatest Integer Function | Smallest Integer Function |
|---|---|
| It is denoted by ⌊x⌋. | It is denoted by ⌈x⌉. |
| If the input is x, then the output is the immediate integer that is less than or equal to x. | If the input is x, then the output is the immediate integer that is greater than or equal to x. |
| It is also known as the floor function. | It is also known as the ceiling function. |
| Examples: ⌊5.3⌋ = 5; ⌊-5.3⌋ = -6 | Examples: ⌈5.3⌉ = 6; ⌈-5.3⌉ = -5 |
Important Notes on Greatest Integer Function:
The following points are helpful to summarize the important points of the greatest integer function.
- If x is a number between successive integers n and n+1, then ⌊x⌋=n. If x is an integer, then ⌊x⌋=x
- The domain of the greatest integer function is ℝ and its range is ℤ.
- The graph of the greatest integer function contains steps made of horizontal lines with one end as an open dot and the other end as a solid dot.
☛Related Topics:
The following links are related to the greatest integer function
FAQs on Greatest Integer Function
What is the Meaning of Greatest Integer Function?
The greatest integer function of x is a function that gives the largest integer which is less than or equal to x. This function is denoted by ⌊x⌋. The given number needs to be rounded off to the nearest integer that is less than or equal to the number itself.
How to Calculate the Greatest Integer Function of a Negative Number?
Let us find the greatest integer function of -3.2. i.e., ⌊-3.2⌋. Don't think that this is equal to -3. By the definition, we have ⌊x⌋ = n, where n ≤ x < n + 1. So think about which integer comes on the immediate left side of -3.2, and the answer is -4. Therefore, ⌊-3.2⌋ = -4.
What is the Other Name of the Greatest Integer Function?
The greatest integer function is also called a floor function. Here the function takes the lowest integral value on rounding the function value and hence it is called a floor function.
How to Graph Greatest Integer Function?
Plotting the graph of the greatest integer function is easy. It is a step curve. Here, f(x) = ⌊x⌋, if x is an integer, then the value of f will be x itself and if x is a non-integer, then the value of x will be the integer just before x. Hence for an integer n, all the numbers of [n, n+1) will have the value of the greatest integer function as n. So for every pair of n and n + 1 on the x-axis, we get a small piece of horizontal line corresponding to y = n. But note that every horizontal line has a closed dot on the left and open dot on the right side.
What is Smallest Integer Function?
The smallest integer function of x is the nearest integer that is greater than or equal to the given number. It is denoted by ⌈x⌉. Here are some examples of smallest integer function's usage.
- ⌈4.2⌉ = 5
- ⌈-2.5⌉ = -2
- ⌈0⌉ = 0
To find the smallest integer function value of a number, just put the number on the number line and pick the very next integer that lies on the right side of the number.
Why is the Greatest Integer Function Not Differentiable?
As we check the graph of the greatest integer function, we can see that it is jumping whenever it reaches an integer. Since the curve is discontinuous at integers, it is not differentiable at those points. Therefore at each integer, the greatest integer function is not differentiable.
Is the Floor Function Differentiable?
The floor function or the greatest integer function is not differentiable at integers. The floor function has jumping values at integers, so its curve is known as the step curve. The curve of floor function is discontinuous at integers and hence not differentiable at integers.
How to Find Greatest Integer Function of a Number?
The easiest way to find the greatest integer function of a number is, just to plot it on the number line and select the first integer that comes on its left side. For example, ⌊4.15⌋ = 4, ⌊-4.15⌋ = -5.
What is the Domain and Range of the Greatest Integer Function?
The input of the greatest integer function can be any real number whereas the greatest integer function's output is always an integer. Thus, the domain of this function is real numbers (ℝ), and its range is integers (ℤ).