Greater Than or Equal to
The greater than or equal to symbol is used to represent inequality in math. It tells us that the given variable is either greater than or equal to a particular value. For example, if x ≥ 3 is given, it means that x is either greater than or equal to 3. It defines a range of values that x can take which starts from 3 and goes up till infinity.
| 1. | What does Greater Than or Equal to Mean? |
| 2. | Greater Than or Equal to Symbol |
| 3. | Greater Than or Equal to Application |
| 4. | FAQs on Greater Than or Equal to |
What Does Greater Than or Equal to Mean?
'Greater than or equal to', as the name suggests, means the variable is either greater than or equal to a particular value. The term 'greater than' is used to express that one quantity is greater than the other quantity. The term 'is equal to' is used to express that two quantities are equal. When these terms are combined with each other they make a new term that is Greater Than Or Equal To and this term is used to show that, the quantity or amount value limit could be equal to or greater than the given limit.
For example, for a person to be elected as president he or she should be a minimum of 35 years old. This means that a person should be either greater than or equal to 35 years old.
Greater Than or Equal to Symbol
The 'Greater than or equal to' symbol is used in linear inequalities when we do not know whether the value of a variable is greater than or equal to a particular value. It is expressed by the symbol '≥'. This symbol is the 'greater than' symbol ( >) with a sleeping line under it. The sleeping line below the greater-than sign means 'equal to'.
Here are a few examples for 'Greater than or equal to'.
- x ≥ 100 means the value of x should be greater than or equal to 100.
- a ≥ - 2 means the value of 'a' should be greater than or equal to -2.
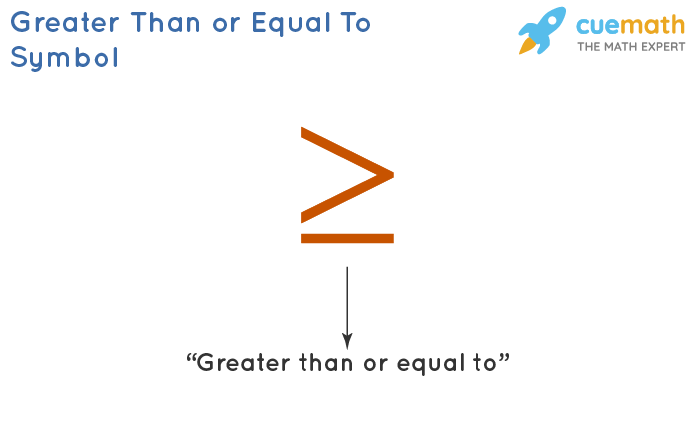
Greater Than or Equal to Application
The 'Greater than or equal to' symbol is used in mathematics to express the relationship between 2 expressions. The following table shows where and how the 'greater than or equal to' symbol is used along with examples and meanings.
| Symbol | Example | Meaning |
|---|---|---|
| Greater than or equal to, ≥ |
x ≥ 2 2 ≥ x ≥ −1 |
The value of x is greater than or equal to 2. The value of x is between -1 and 2 inclusive of both values. |
☛Related Articles
Greater Than or Equal to Examples
-
Example 1: If the value of x is greater than or equal to 9, how will this be shown in an expression?
Solution:
The statement says that the value of x is greater than or equal to 9. So this can be expressed as, x ≥ 9
-
Example 2: State true or false:
a.) If the value of 'a' is greater than or equal to 10, this can be expressed as, a ≥ 10
b.) 6 ≥ x ≥ -1 means that the value of x is between -1 and 6 inclusive of both values.
Solution:
a.) True, if the value of 'a' is greater than or equal to 10, this can be expressed as, a ≥ 10
b.) True, 6 ≥ x ≥ -1 means that the value of x is between -1 and 6 inclusive of both values.
-
Example 3: What does the following expression mean? x ≥ 3 where x ∈ N?
Solution: We know that N is the symbol for the set of natural numbers like 1, 2, 3, 4, and so on
It is given that x ≥ 3 and x ∈ N
This means that x is a natural number that is greater than or equal to 3.

FAQs on Greater Than or Equal to
What is Greater Than or Equal to in Math?
Greater than or equal to, as the name suggests, means something is either greater than or equal to some quantity. Greater than or equal to is represented by the symbol "≥". For example, x ≥ −2 means the value of x is greater than or equal to -2.
What is the Symbol for Greater Than or Equal to?
The symbol of 'greater than or equal to' looks like '≥ '. The open side of the symbol should be in front of the bigger value. The line below the symbol shows that the value could be equal to or more than the limit. For example, x ≥ 5.
Here, the value of x should either equal to or more than 5.
How do you Explain Greater Than or Equal to?
Greater than or equal to is something either greater than or equal to a given quantity. For example, if a florist earns $5 or more than $5 in a day, then it can be either $5, or more than $5. Now, if we assume the earning to be x, then this can be expressed as x ≥ $5.
What is the Difference Between Greater Than and Greater Than or Equal to?
The greater than symbol is written as > whereas the greater than or equal to is represented as ≥. 'Greater than' means that some variable or number can have any value that is greater than the given limit. Whereas the 'greater than or equal to' symbol states that the number or variable can be equal to or more than the given limit.
What is the Difference Between Greater Than or Equal to and Less Than or Equal to?
The 'greater than or equal to' sign tells that the amount is either more than or equal to the minimum limit whereas the 'less than or equal to' sign is just the opposite of this sign. Less than or equal to means, the amount is equal to or less than the maximum limit.
What is the Difference Between Greater Than or Equal to and Equal to?
The 'Greater than or equal to' ( ≥) symbol signifies that the value is either more than or equal to the given limit; whereas the equal to (=) symbol means the quantity is fixed. It is neither less than nor greater than the given value, it is exactly equal to the value.
Is 4 Greater Than or Equal to 3?
No, we cannot say that 4 is greater than or equal to 3. Because 4 is bigger than 3 and not equal to 3. Therefore, the correct sentence will be 4 is greater than 3.
What is the use of Greater Than or Equal to?
Greater than or equal to is used to show that one variable is greater than or equal to a given quantity. For example, if a company has a policy to launch the product either at the same price or more than the old price. It can be said that the new product price is greater than or equal to the old price.
What is the Solution to 3x + 2.4 Greater than or Equal to 3.0?
In order to solve this inequality, we need to write it in the form of a mathematical expression, that is, 3x + 2.4 ≥ 3.0. After this, we can solve for the value of x and we get the result as follows.
3x + 2.4 ≥ 3.0
3x ≥ 3.0 - 2.4
3x ≥ 0.6
x ≥ 0.2
This means the value of x is greater than or equal to 0.2
visual curriculum