Product Rule
Product rule in calculus is a method to find the derivative or differentiation of a function given in the form of the product of two differentiable functions. That means, we can apply the product rule, or the Leibniz rule, to find the derivative of a function of the form given as: f(x)·g(x), such that both f(x) and g(x) are differentiable. The product rule follows the concept of limits and derivatives in differentiation directly. Let us understand the product rule formula, its proof using solved examples in detail in the following sections.
What is the Product Rule?
Product rule in calculus is a method used to find the derivative of any function given in the form of a product obtained by the multiplication of any two differentiable functions. The product rule in words states that the derivative of a product of two differentiable functions is equal to the sum of the product of the second function with differentiation of the first function and the product of the first function with the differentiation of the second function. That means if we are given a function of the form: f(x)·g(x), we can find the derivative of this function using the product rule derivative as,
\(\frac{d}{dx}\) f(x)·g(x) = [g(x) × f'(x) + f(x) × g'(x)]
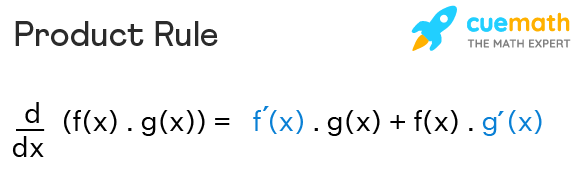
Product Rule Formula
We can calculate the derivative or evaluate the differentiation of the product of two functions using the product rule formula in Calculus. The product rule formula is given as,
\(\frac{d}{dx}\) f(x) = \(\frac{d}{dx}\) {u(x)·v(x)} = [v(x) × u'(x) + u(x) × v'(x)]
where,
- f(x) = Product of differentiable functions u(x) and v(x)
- u(x), v(x) = Differentiable functions
- u'(x) = Derivative of function u(x)
- v'(x) = Derivative of the function v(x)
Derivation of Product Rule Formula
In the previous section, we learned about the product formula to find derivatives of the product of two differentiable functions. For any two functions, product rule may be given in Lagrange's notation as
(u v)' = u'·v + u·v'
or in Leibniz's notation as
\(\dfrac {d}{dx}\) (u·v) = \(\dfrac {du}{dx}\)·v + u·\(\dfrac {dv}{dx}\)
Let us see the proof of the product rule formula here. There are different methods to prove the product rule formula, given as,
- Using the first principle
- Using chain rule
Product Rule Formula Proof Using First Principle
To prove product rule formula using the definition of derivative or limits, let the function h(x) = f(x)·g(x), such that f(x) and g(x) are differentiable at x.
⇒ h'(x) = \(\mathop {\lim }\limits_{Δx \to 0}\) [h(x + Δx) - h(x)]/Δx
= \(\mathop {\lim }\limits_{Δx \to 0}\) \(\frac{f(x+Δx)g(x+Δx) - f(x)g(x)}{Δx}\)
= \(\mathop {\lim }\limits_{Δx \to 0}\) \(\frac{f(x+Δx)g(x+Δx) - f(x)g(x+Δx) + f(x)g(x+Δx) - f(x)g(x)}{Δx}\)
= \( \mathop {\lim }\limits_{Δx \to 0} \frac{[f(x+Δx) - f(x)]g(x+Δx) + f(x)[g(x+Δx) - g(x)]}{Δx}\)
= \( \mathop {\lim }\limits_{Δx \to 0} \frac{[f(x+Δx) - f(x)]g(x+Δx)}{Δx} + \mathop {\lim }\limits_{Δx \to 0} \frac{f(x)[g(x+Δx) - g(x)]}{Δx}\)
= \( (\mathop {\lim }\limits_{Δx \to 0} \frac{[f(x+Δx) - f(x)]}{Δx})( \mathop {\lim }\limits_{Δx \to 0} g(x+Δx) )+ (\mathop {\lim }\limits_{Δx \to 0}f(x)) (\mathop {\lim }\limits_{Δx \to 0} \frac{[g(x+Δx) - g(x)]}{Δx})\)
= \( g(x)\mathop {\lim }\limits_{Δx \to 0} \frac{[f(x+Δx) - f(x)]}{Δx} + f(x)\mathop {\lim }\limits_{Δx \to 0}\frac{[g(x+Δx) - g(x)]}{Δx}\)
∵ \(\mathop {\lim }\limits_{Δx \to 0} \frac{[f(x+Δx) - f(x)]}{Δx}\) = f'(x) and \(\mathop {\lim }\limits_{Δx \to 0}\frac{[g(x+Δx) - g(x)]}{Δx}\) = g'(x)
⇒ \(\frac{d}{dx}\) f(x)·g(x) = [g(x) × f'(x) + f(x) × g'(x)]
Hence, proved.
Product Rule Formula Proof Using Chain Rule
We can derive the product rule formula in calculus using the chain rule formula by considering the product rule as a special case of the chain rule. Let f(x) be a differentiable function such that h(x) = f(x)·g(x).
\(\frac{d}{dx}\) (f·g) = [δ(fg)/δf][df/dx] + [δ(fg)/δg][dg/dx] = g(df/dx) + f(dg/dx)
Hence, proved.
Product Rule for Product of More Than Two Functions
The product rule can be generalized to products of more than two factors using the same product rule formula. For example, for three functions, u(x), v(x), and w(x), product given as u(x)v(x)w(x), we have,
\( \frac{d(uvw)}{dx}=\frac{du}{dx}vw+u\frac {dv}{dx}w+uv\frac {dw}{dx}{\frac {d(uvw)}{dx}}={\frac {du}{dx}}vw+u{\frac {dv}{dx}}w+uv{\frac {dw}{dx}}\)
How to Apply Product Rule in Differentiation?
In order to find the derivative of the function of the form h(x) = f(x)g(x), both f(x) and g(x) should be differentiable functions. We can apply the following given steps to find the derivation of a differentiable function h(x) = f(x)g(x) using the product rule.
- Step 1: Note down the values of f(x) and g(x).
- Step 2: Find the values of f'(x) and g'(x) and apply the product rule formula, given as: h'(x) = \(\frac{d}{dx}\) f(x)·g(x) = [g(x) × f'(x) + f(x) × g'(x)]
Let us have a look at the following example given below to understand the product rule better.
Example: Find f'(x) for the following function f(x) using the product rule: f(x) = x·log x.
Solution:
Here, f(x) = x·log x
u(x) = x
v(x) = log x
⇒u'(x) = 1
⇒v'(x) = 1/x
⇒f'(x) = [v(x)u'(x) + u(x)v'(x)]
⇒f'(x) = [log x•1 + x•(1/x)]
⇒f'(x) = log x + 1
Answer: The derivative of x log x using the product rule is log x + 1.
☛ Topics Related to Product Rule:
Examples on Product Rule
-
Example 1: Find the derivative of x· cos(x) using the product rule formula.
Solution:
Let f(x) = cos x and g(x) = x.
⇒f'(x) = -sin x
⇒g'(x) = 1⇒[f(x)g(x)]' = [g(x)f'(x) + f(x)g'(x)]
⇒[f(x)g(x)]' = [(x•(-sin x) + cos x•(1)]
⇒[f(x)g(x)]' = - x sin x + cos xAnswer: The derivative of x cos x using product rule is (- x sin x + cos x).
-
Example 2: Differentiate x2 log x using the product rule formula.
Solution:
Let f(x) = log x and g(x) = x2.
⇒f'(x) = (1/x)
⇒g'(x) = 2x⇒[f(x)g(x)]' = [g(x)f'(x) + f(x)g'(x)]
⇒[f(x)g(x)]' = [(x2•(1/x) + log x•(2x)]
⇒[f(x)g(x)]' = x + 2x log xAnswer: The derivative of x2 log x using product rule is (x + 2x log x).
-
Example 3: Apply the product rule to differentiate (1 - 2x)·sin x.
Solution:
Let f(x) = (1-2x), g(x) = sin x
⇒g'(x) = cos x
⇒f'(x) = -2⇒[f(x)g(x)]' = [g(x)f'(x) + f(x)g'(x)]
⇒[f(x)g(x)]' = [(sin x•(-2) + (1 - 2x)•(cos x)]
⇒[f(x)g(x)]' = - 2 sin x + cos x - 2x cos xAnswer: The derivative of (1 - 2x)·sin x using product rule is - 2 sin x + cos x - 2x cos x.

FAQs on Product Rule
What is Product Rule of Differentiation in Calculus?
The product rule is one of the derivative rules that we use to find the derivative of functions of the form P(x) = f(x)·g(x). The derivative of a function P(x) is denoted by P'(x). If the derivative of the function P(x) exists, we say P(x) is differentiable, that means, differentiable functions are those functions whose derivatives exist. A function P(x) is differentiable at a point x = a if the following limit exists.
\(P'(x) = \mathop {\lim }\limits_{h \to 0} \frac{P(a+h)-P(a)}{h}\)
How to Find Derivative Using Product Rule?
The derivatives of the product of two differentiable functions can be calculated in calculus using the product rule. We need to apply the product rule formula for differentiation of function of the form, f(x) = u(x)v(x). The product rule formula is given as,
f'(x) = [u(x)v(x)]' = [u'(x) × v(x) + u(x) × v'(x)]
where, f'(x), u'(x) and v'(x) are derivatives of functions f(x), v(x) and u(x).
What is Product Rule Formula?
Product rule derivative formula is a rule in differential calculus that we use to find the derivative of product of two or more functions. Suppose two functions, u(x) and v(x) are differentiable, then the product rule can be applied to find (d/dx)[u(x)v(x)] as,
f'(x) = [u(x)v(x)]' = [u'(x) × v(x) + u(x) × v'(x)]
How to Derive the Formula for Product Rule?
Product rule formula can be derived using different methods. They are given as,
- Using derivative and limit properties or first principle
- Using chain rule
Click here to check the detailed proof of product formula.
How to Use Product Rule in Differentiation?
Product rule can be used in finding the differentiation of a function f(x) of the form u(x)v(x). Derivative of this function using product rule can be given as, f'(x) = [u(x)v(x)]' = [u'(x) × v(x) + u(x) × v'(x)]
How to Derive Product Rule Using Definition of Limits and Derivatives?
The proof of the product rule can be given using the definition and properties of limits and derivatives. For a function f(x) = u(x)·v(x), the derivative f'(x) can be given as,
⇒ h'(x) = \(\mathop {\lim }\limits_{Δx \to 0}\) [h(x + Δx) - h(x)]/Δx
= \(\mathop {\lim }\limits_{Δx \to 0}\) \(\frac{f(x+Δx)g(x+Δx) - f(x)g(x)}{Δx}\)
= \(\mathop {\lim }\limits_{Δx \to 0}\) \(\frac{f(x+Δx)g(x+Δx) - f(x)g(x+Δx) + f(x)g(x+Δx) - f(x)g(x)}{Δx}\)
= \( \mathop {\lim }\limits_{Δx \to 0} \frac{[f(x+Δx) - f(x)]g(x+Δx) + f(x)[g(x+Δx) - g(x)]}{Δx}\)
= \( \mathop {\lim }\limits_{Δx \to 0} \frac{[f(x+Δx) - f(x)]g(x+Δx)}{Δx} + \mathop {\lim }\limits_{Δx \to 0} \frac{f(x)[g(x+Δx) - g(x)]}{Δx}\)
= \( (\mathop {\lim }\limits_{Δx \to 0} \frac{[f(x+Δx) - f(x)]}{Δx})( \mathop {\lim }\limits_{Δx \to 0} g(x+Δx) )+ (\mathop {\lim }\limits_{Δx \to 0}f(x)) (\mathop {\lim }\limits_{Δx \to 0} \frac{[g(x+Δx) - g(x)]}{Δx})\)
= \( g(x)\mathop {\lim }\limits_{Δx \to 0} \frac{[f(x+Δx) - f(x)]}{Δx} + f(x)\mathop {\lim }\limits_{Δx \to 0}\frac{[g(x+Δx) - g(x)]}{Δx}\)
∵ \(\mathop {\lim }\limits_{Δx \to 0} \frac{[f(x+Δx) - f(x)]}{Δx}\) = f'(x) and \(\mathop {\lim }\limits_{Δx \to 0}\frac{[g(x+Δx) - g(x)]}{Δx}\) = g'(x)
⇒ \(\frac{d}{dx}\) f(x)·g(x) = [g(x) × f'(x) + f(x) × g'(x)]
What are Applications of Product Rule Derivative Formula? Give Examples.
We can apply the product rule to find the differentiation of the function of the form u(x)v(x). For example, for a function f(x) = x2 sin x, we can find the derivative as, f'(x) = sin x·2x + x2·cos x.
How to Find Derivative of Product of More Than Two Functions Using Product Rule?
We can generalize the formula for differentiation of products of more than two functions using the same product rule formula. For example, for three functions, u(x), v(x), and w(x), product given as u(x)v(x)w(x), we have,
\( \frac{d(uvw)}{dx}=\frac{du}{dx}vw+u\frac {dv}{dx}w+uv\frac {dw}{dx}{\frac {d(uvw)}{dx}}={\frac {du}{dx}}vw+u{\frac {dv}{dx}}w+uv{\frac {dw}{dx}}\)
How Can we Verify Quotient Rule Using the Product Rule in Calculus?
To prove the quotient rule using the product rule and chain rule, we can express the function f(x) = u(x)/v(x) as f(x) = u(x)•1/v(x) and further apply product rule formula to find f'(x) = (1/v(x))u'(x) - u(x)•(1/v(x))2•v'(x) = \(\frac{u'(x)v(x) - u(x)v'(x)}{[v(x)]^2}\).
visual curriculum