Quotient
Quotient is the answer obtained when we divide one number by another. For example, if we divide the number 6 by 3, we get the result as 2, which is the quotient. The quotient can be an integer or a decimal number. For exact divisions such as 10 ÷ 5 = 2, we have an integer as a quotient, and for divisions such as 12 ÷ 5 = 2.4, the quotient is a decimal. A quotient can be larger than the divisor but it is always smaller than the dividend. Let us explore and know more about the quotient and the methods to find the quotient.
| 1. | What is Quotient in Division? |
| 2. | Quotient Definition |
| 3. | How to Find the Quotient? |
| 4. | Quotient Divisor Dividend |
| 5. | Quotient and Remainder |
| 6. | FAQs on Quotient |
What is Quotient in Division?
Quotient is the final answer that we get when we divide a number. Division is a method of distributing objects equally in groups and it is denoted by a mathematical symbol (÷). For example, there are 15 balls that need to be divided equally into 3 groups. So, when we divide these balls into 3 equal groups, the division statement can be expressed as, 15 ÷ 3 = 5. Here, 5 is the quotient. This means that in each group there will be 5 balls.
Quotient Definition
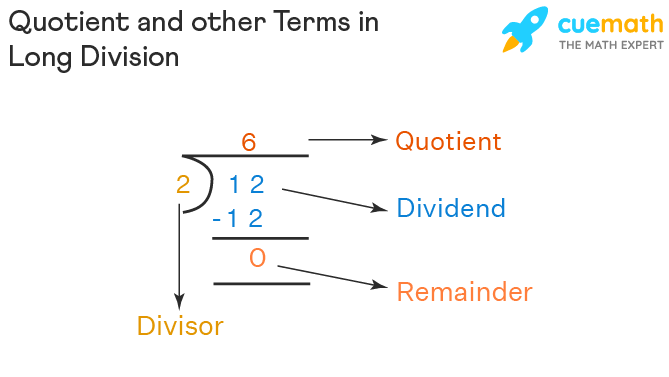
Quotient, in mathematics, can be defined as the result of the division of a number by any divisor. It is the number of times the divisor is contained in the dividend. The following figure shows the statement of division which marks the divisor, the dividend and the quotient. The divisor, 2 is contained 6 times in the dividend, 12. The quotient can be larger or smaller than the divisor but it is always smaller than the dividend.

How to Find the Quotient?
The quotient is obtained after the process of division is completed. This means when a divisor divides a dividend, the answer that we get is the quotient. Division is one of the four basic mathematical operations, the other three being addition, subtraction, and multiplication. The quotient is the result of the division process. After we divide a number completely, we get the quotient. In certain cases, when we divide a number, the number does not get divided completely and we get a remainder. However, even in this case, there is a quotient that remains as the answer and we mention the remainder separately.
Quotient Divisor Dividend
When we divide a number, there are other terms that are used in the process of division, apart from the quotient. Let us understand this with the help of an example. For example, there is a chocolate bar with 12 pieces. Can the bar be divided equally between two friends? The answer is yes, once the chocolate bar is divided equally between 2 friends, each friend will get 6 pieces of the chocolate. Did you notice that no piece of chocolate remains unshared. Hence, there is no remainder. We can write the division statement for this example as 12 ÷ 2 = 6. Here, each of the numbers in the division can be designated with special terms. Let us check the following terms closely related to the quotient.
| Terms | Descriptions | Values |
|---|---|---|
| Dividend | The total pieces that are to be shared. | 12 |
| Divisor | The number of equal groups that are to be made. | 2 |
| Quotient | The number of pieces in each group. | 6 |
| Remainder | The remaining piece that is not part of any group. | 0 |
This example can also be mathematically represented as follows:
Quotient and Remainder
When we divide a number and if it does not get divided completely, we are left with a remainder. Let us understand this with the help of an example. The quotient can be calculated by dividing the dividend with the divisor. Quotient = Dividend ÷ Divisor. Let us solve 435 ÷ 4. Here, 435 is the dividend and 4 is the divisor.
The following steps are helpful to understand the division process and to find the quotient and the remainder.
- Step 1: Take the first digit of the dividend. If this digit is greater than or equal to the divisor, then divide it by the divisor and write the answer on top as a part of the quotient. Multiply this number with the divisor and write the product below the first digit of the dividend. Subtract the result from the digit and write it below that number. Here, the first digit is 4 and it is equal to the divisor. So, 4 ÷ 4 = 1 is written on top of the bar. The product of 4 × 1 = 4 is subtracted from the digit and 0 is written below. Now, bring down the next number of the dividend which is 3 and place it next to 0.
- Step 2: We can see that we have 3 as the result of step 1. Repeat the same step of checking if this number is greater or smaller than the divisor. Since 3 is less than 4, we cannot divide this number. Hence, we write a 0 on the top and write the product of 4 × 0 = 0 below the 3, then subtract 3 - 0 = 3. The next step is to bring down the next number from the dividend and place it beside 3. This makes it 35. As 35 > 4, we can divide this number by 4. After writing 8 on top, we write the product of 4 × 8 = 32 below 35 as shown. Subtract 35 - 32 = 3. Now, this 3 is smaller than the divisor 4 and there is no number left to be brought down from the dividend. This means we will leave 3 as the remainder and complete the division. Therefore, 3 is known as the remainder and 108 is called the quotient.

Verification of the Division Result
We can easily verify if the answer that we obtained in the long division is correct or not. As the process of division is the reverse of multiplication, let us find out how we can verify our answer using this information. We use the formula, Dividend = (Divisor × Quotient) + Remainder. This means if we multiply the divisor with the quotient and add the remainder we should get the number as the dividend. If the numbers satisfy this equation, then the answer is considered to be correct, otherwise, we need to check our division. Let us reconsider the example discussed above. Here, the dividend is 435, the divisor is 4, the quotient is 108, and the remainder is 3. Substituting the value in the formula, we get 435 = (4 × 108) + 3. This proves that the answer is correct. Let us take another example. If we divide 6 ÷ 2 = 3, we have the remainder as 0. Now, let us substitute these values in the formula, 6 = (2 × 3) + 0. This means the answer is correct.
Estimating Quotient
Estimating the quotient means finding the quotient after rounding off the divisor and dividend. The idea is to convert the given numbers to such numbers that are easy to compute. Let us understand this with an example using the following steps. Let us divide 64 ÷ 22
- Step 1: We need to divide 64 ÷ 22. Here, 64 is the dividend and the divisor is 22 and we need to estimate the quotient.
- Step 2: We first need to round off the dividend 64 to the nearest tens because the last place value here is tens. After checking the digit at ones place, it will be rounded down to 60 because the digit at ones place (that is 4) is less than 5. Similarly, the divisor will also be rounded off to the nearest tens because in 22, the last place value is tens. So we need to check the digit in ones place (that is 2) which is less than 5. Therefore, 22 will be rounded down to 20.
- Step 3: Now, we have rounded the given numbers and it has become 60 ÷ 20. We can simply divide it and we get 3 as the estimated quotient.
- Step 4: Another method to estimate the quotient is to eliminate the least number of zeros in the estimated (rounded) divisor and the estimated (rounded) dividend. So, in this case, after eliminating the least number of zeros, 60 ÷ 20 becomes 6 ÷ 2 and we get the quotient as 3. So, we got the same estimated quotient by both the methods.
Example: Estimate the quotient of 825 divided by 24.
Solution: In the given question, we need to divide 825 ÷ 24.
- Step 1: We need to round off the divisor and the dividend. Since in 825, the last place value is hundreds, we need to round it off to the nearest hundreds. For this, we need to check the digit on tens place. Here, it is 2, which is less than 5. So 825 will be rounded down to 800. Similarly, since in 24, the last place value is tens, we need to round it off to the nearest tens. For this, we need to check the digit on ones place. Here, it is 4, which is less than 5. So 24 will be rounded down to 20.
- Step 2: Now, we need to divide 800 ÷ 20, which can be simply divided and we get the estimated quotient as 40.
☛ Related Articles
Examples on Quotient
-
Example 1: $4000 is distributed among 25 workers for the work completed by them at a construction site. Calculate the amount given to each worker.
Solution:
The total amount to be distributed = $4000. The number of workers = 25. We need to calculate the amount given to each worker. To do so, we will divide 4000 by 25 using the long division method and find the quotient.

The quotient that we get is 160. Therefore, the amount given to each worker is $160.
-
Example 2: Divide 66 ÷ 7 and find the quotient and remainder.
Solution:
We will use the long division method to find the quotient.

After dividing 66 by 7 we get 9 as the quotient and 3 as the remainder.
-
Example 3: State true or false
a.) Quotient is the final answer that we get when we divide a number.
b.) When we divide a number and if it does not get divided completely, we are left with a remainder.
Solution:
a.) True, quotient is the final answer that we get when we divide a number.
b.) True, when we divide a number and if it does not get divided completely, we are left with a remainder.

FAQs on Quotient
What is Quotient in Math?
Quotient is the final answer that we get when we divide a number. For example, if we divide 63 ÷ 9, we get the answer as 7. Here, 7 is called the quotient. It should be noted that the quotient can be larger or smaller than the divisor but is always smaller than the dividend.
How to Find the Quotient in Division?
The quotient is obtained after the process of division is completed. This means when a divisor divides a dividend, the answer that we get is the quotient. In other words, the quotient can be found using the formula, Dividend ÷ Divisor = Quotient. Let us understand this by a simple example of 12 ÷ 4 = 3. Here 12 is the dividend, 4 is the divisor, and 3 is the quotient.
Is Quotient Always a Whole Number?
No, the quotient may not always be a whole number. The quotient can be a whole number or a decimal number. For a perfect division, such as 16 ÷ 2 = 8, the quotient is a whole number and for numbers in which we are left with a remainder, we divide the number further by placing a decimal in the quotient. Therefore, in these cases, the quotient becomes a decimal number. For example, if we divide 16 ÷ 5, we get 3.2 as the quotient which is a decimal number.
What is the Difference Between Quotient and Remainder?
Quotient is the answer that we get when we divide a number. The number that is left after the division is over is called the remainder. It refers to the remaining part, after the completion of the division process. For example, if we need to distribute 7 balls among 2 children equally, we give 3 balls to each child and we are left with 1 ball. This 1 ball is the remainder. Mathematically, the number 7 cannot be completely divided by the number 2. After division, the number 1 is left as the remainder. For perfect divisions, the quotient is a whole number, and the remainder is zero.
How Can we Verify the Quotient in Division?
Division is also known as inverse multiplication. We can verify the quotient by using the following formula:
Dividend = (Divisor × Quotient) + Remainder
This means if we multiply the divisor with the quotient and add the remainder we should get the number as the dividend. If the numbers satisfy this equation, then the answer is considered to be correct, otherwise, we need to check our division.
How to Find the Quotient When the Remainder and Divisor is given?
If the remainder, divisor, and dividend is given we can easily find the quotient by substituting the values in the formula, Dividend = (Divisor × Quotient) + Remainder. After we substitute the known values we can get the value of the quotient.
What is the Quotient of 21 Divided by 7?
When 21 is divided by 7 the quotient is 3. The number 21 is the dividend and the number 7 is the divisor and 3 is the quotient.
What is the Difference Between Quotient and Product?
'Quotient' is the result of division whereas 'product' is the result of multiplication. The quotient is smaller than the dividend and the divisor. The product is larger than the numbers that are multiplied.
How to Estimate the Quotient?
In order to estimate the quotient, we need to first round off the divisor and the dividend and then divide them. For example, if we need to estimate the quotient for 84 ÷ 18, we will round these. Now, 84 will be rounded down to 80 and 18 will be rounded up to 20. So, we get, 80 ÷ 20 and the answer will be 4. Therefore, the estimated quotient is 4 in this case.
visual curriculum