Cotangent
Cotangent is one of the 6 trigonometric functions. It is usually referred to as "cot". Just like other trigonometric ratios, the cotangent formula is also defined as the ratio of the sides of a right-angled triangle. The cot x formula is equal to the ratio of the base and perpendicular of a right-angled triangle. Here are 6 basic trigonometric functions and their abbreviations.
| Trigonometric Function | Abbreviation |
|---|---|
| Sine Function | sin |
| Cosine Function | cos |
| Tangent Function | tan |
| Cosecant Function | csc |
| Secant Function | sec |
| Cotangent Function | cot |
Let us learn more about cotangent by learning its definition, cot x formula, its domain, range, graph, derivative, and integral. Also, we will see what are the values of cotangent on a unit circle.
What is Cotangent?
Cotangent is one of the basic trigonometric ratios. It is, in fact, one of the reciprocal trigonometric ratios csc, sec, and cot. It is usually denoted as "cot x", where x is the angle between the base and hypotenuse of a right-angled triangle. Alternative names of cotangent are cotan and cotangent x. The cotangent of an angle in a right triangle is defined as the ratio of the adjacent side (the side adjacent to the angle) to the opposite side (the side opposite to the angle).
Cotangent Formula
The cotangent formula for an angle θ is: cot θ = (Adjacent side) / (Opposite side). Let us take a look at the right-angled triangle ABC that is right-angled at B. Then AB is the side that is adjacent to A and BC is the side that is opposite to A. Then cotangent of A (which is written as cot A) is,
cot A = (Adjacent side of A) / (Opposite side of A) = (AB) / (BC).

For example, if AB = 3 and BC = 4, then cot A = 3/4.
Properties of Cotangent
We already know that cot x = (Adjacent) / (Opposite). Apart from this, there are several other formulas of cotangent ratio where cotangent can be written in terms of other trigonometric ratios.
Cotangent in Terms of Cos and Sin
We know that sin θ = (Opposite) / (Hypotenuse) and cos θ = (Adjacent) / (Hypotenuse). If we divide cos θ by sin θ , we get
(cos θ) / (sin θ) = (Adjacent) / (Hypotenuse) × (Hypotenuse) / (Opposite)
= (Adjacent) / (Opposite)
= cot θ
Therefore, cot θ = (cos θ) / (sin θ) is the cot x formula in terms of cos and sin.
Cotangent in Terms of Tan
We know that tan θ = (Opposite)/(Adjacent) and cot θ = (Adjacent)/(Opposite). Thus, cot and tan are reciprocals of each other. Thus, we can write cot θ = 1/tan θ and tan θ = 1/cot θ. Thus, cot in terms of tan is. cot θ = 1/tan θ. There is another formula to write cot in terms of tan which is, cot θ = tan (π/2 - θ) (or) tan(90° - θ).
Cotangent in Terms of Cosec
From one of the Pythagorean identities, csc2θ - cot2θ = 1. From this, we get cot2θ = csc2θ - 1. If we take square root on both sides, cot θ = √(csc2θ - 1). Therefore, cot in terms of csc is, cot θ = √(csc2θ - 1)
Cotangent Law
Consider a triangle ABC where AB = c, BC = a, and CA = b. The cotangent law looks like sine law but it involves the half angles. The cotangent law says, (cot A/2) / (s - a) = (cot B/2) / (s - b) = (cot C/2) / (s - c). Here, 's' is the semi-perimeter of the triangle. i.e., s = (a + b + c)/2.
Sign of Cotangent
The cotangent ratio (of course, both tan and cot) is positive only in the first and third quadrants. It is negative in the second and fourth quadrants. Thus,
- cot (π - θ) = - cot θ (2nd quadrant)
- cot (π + θ) = cot θ (3rd quadrant)
- cot (2π - θ) = - cot θ (4th quadrant)
- cot (2π + θ) = cot θ (1st quadrant)
Period of Cotangent
We know that all trigonometric functions are periodic functions. Also, from the previous section, we know that cot (2π + θ) = cot θ. But the cotangent function can have a smaller period π (as the cotangent function is positive in the first and third quadrants where the angles on the third quadrant are π + the angle in the first quadrant). Thus, the period of cotangent is π. i.e., cot (π + θ) = cot θ.
Cotangent of Negative Angle
The cotangent of a negative angle is the negative of the cotangent of a positive angle. i.e., cot (-x) = -cot x, for any x in the domain. From this, we can conclude that cotangent is an odd function.
Cotangent on Unit Circle
We know that each point on the unit circle gives the values of cos and sin of the corresponding angle. To find the cotangent of the corresponding angle, we just divide the corresponding value of cos by the corresponding value of sin because we have cot x formula given by, cot x = (cos x) / (sin x). Here, we can see the values of cot θ for some standard angles.

In the same way, we can calculate the cotangent of all angles of the unit circle. Here is the unit circle with the cotangent function.
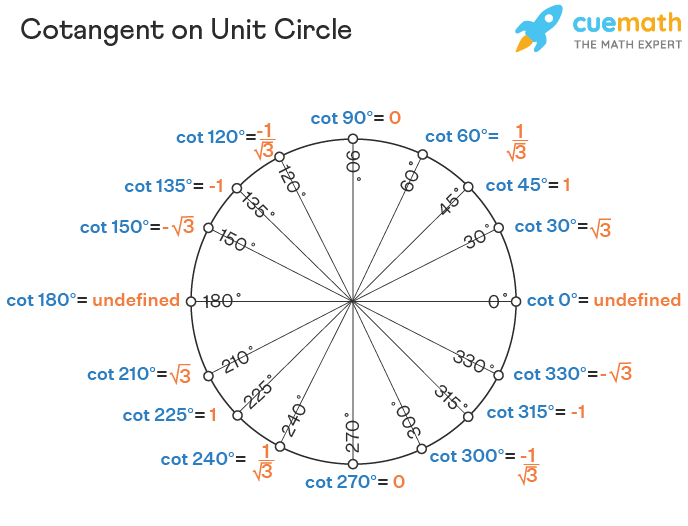
Domain, Range, and Graph of Cotangent
In this section, let us see how we can find the domain and range of the cotangent function. Also, we will see the process of graphing it in its domain.
Domain and Range of Cotangent
In the previous section, we have seen that cot is not defined at 0° (0π), 180° (1π), and 360° (2π) (in other words, cotangent is not defined wherever sin x is equal to zero because cot x = (cos x)/(sin x)). We know that sin x is equal to zero for integer multiples of π, therefore the cotangent function is undefined for all integer multiples of π. Thus, cot nπ is NOT defined for any integer n. Thus, the domain of cotangent is the set of all real numbers (R) except nπ (where n ∈ Z). Again, from the unit circle, we can see that the cotangent function can result in all real numbers, and hence its range is the set of all real numbers (R). Thus,
- The domain of cotangent is the set of real numbers except for all the integer multiples of π
- The range of cotangent is the set of all real numbers
i.e., cot x : R - {nπ / n ∈ Z} → R
Graph of Cotangent
Since the cotangent function is NOT defined for integer multiples of π, there are vertical asymptotes at all multiples of π in the graph of cotangent. Also, from the unit circle (in one of the previous sections), we can see that cotangent is 0 at all odd multiples of π/2. Also, from the unit circle, we can see that in an interval say (0, π), the values of cot decrease as the angles increase. Hence cot is a decreasing function. Thus, the graph of the cotangent function looks like this.

Derivative and Integral of Cotangent
To find the derivative and the integral of cotangent, we use the identity cotangent formula cot x = (cos x) / (sin x). Let us see how.
Derivative of Cotangent
Let y = cot x = (cos x) / (sin x). Then by quotient rule,
y' = [ sin x d/dx(cos x) - cos x d/dx(sin x) ] / (sin x)2
= [ sin x (- sin x) - cos x (cos x) ] / sin2x
= [-sin2x - cos2x] / sin2x
= - [sin2x + cos2x] / sin2x
= -1/sin2x --- [Using trigonometric identity sin2x + cos2x = 1]
= -csc2x --- [Because sin x = 1/csc x and csc x = 1/sin x]
Thus, the derivative of cot x is -csc2x.
Integral of Cotangent
∫ cot x = ∫ (cos x) / (sin x) dx
We will evaluate this integral by substitution method. For this, let sin x = u. Then cos x dx = du.
Then using the above integral becomes,
∫ (1/u) du = ln |u| + C, where C is the integration constant.
Substitute u = sin x back here,
∫ cot x dx = ln |sin x| + C
Thus, the integral of cot x is ln |sin x| + C.
Important Points on Cotangent:
- Cot x Formula: cot x = (cos x) / (sin x)
- Some important cotangent formulas are:
cot x = (cos x)/(sin x)
cot x = 1/tan x
cot (-x) = - cot x
cot θ = √(csc2θ - 1) - The domain of cot x is R - {nπ} and its range is R.
- Cotangent function has vertical asymptotes at all multiples of π.
Topics Related:
Examples on Cotangent
-
Example 1: Find the cotangent of x if sin x = 3/5 and cos x = -4/5 using the cotangent formula
Solution:
We know that cot x = (cos x) / (sin x)
= (-4/5) / (3/5)
= -4/3
Answer: cot x = -4/3.
-
Example 2: Prove the identity: csc x / (tan x + cot x) = cos x.
Solution:
Here we use the formula of cotangent which is cot x = (cos x) / (sin x) and the formula of tangent which is tan x = (sin x)/ (cos x). Also, csc x = 1/sin x. Then we get
LHS = csc x / (tan x + cot x)
= (1/sin x) / (sin x/cos x + cos x/sin x)
= (1/sin x) / [ (sin2x + cos2x)/sin x cos x ]
= (1/sin x) / (1/sin x cos x) --- [Because sin2x + cos2x = 1]
= (1/sin x) × (sin x cos x)/1
= cos x
= RHS
Answer: We have proved the identity csc x / (tan x + cot x) = cos x.
-
Example 3: Evaluate cot (x - π) + cot (2π - x) + cot x.
Solution:
We use the following cotangent formulas to solve this.
cot (-x) = - cot x
cot (π - x) = - cot x
cot (2π - x) = - cot x
Then we get:
cot (x - π) + cot (2π - x) + cot x
= - cot (π - x) + cot (2π - x) + cot x
= - (-cot x) - cot x + cot x
= cot x
Answer: cot (x - π) + cot (2π - x) + cot x = cot x.

FAQs on Cotangent
What is Cotangent in Trigonometry?
The cotangent is one of the trigonometric ratios and is defined as cot x = (adjacent side)/(opposite side) for any angle x between the base and hypotenuse in a right-angled triangle.
What are Cotangent Formulas?
Some of the important cot x formulas are:.
- cot x = (adjacent)/(opposite)
- cot x = (cos x)/(sin x)
- cot x = 1/tan x
- cot (π/2 - x) = tan x
- cot (π + x) = cot x
- cot (2π + x) = cot x
- cot (-x) = - cot x
- cot θ = √csc²θ - 1
Is Cotangent the Inverse of Tangent?
No, the inverse of tangent is arctan. It is written as tan-1. But (tan x)-1 = 1/tan x = cot x. (tan x)-1 and tan-1x are NOT the same.
What is the Domain and Range of Cotangent?
The domain of cotangent is R - {nπ, where n is an integer} and the range of cotangent is R. Here, R is the set of all real numbers.
What is the Opposite of Cotangent Formula?
We do not use the terminology of saying opposite of cotangent. However
- The reciprocal of cotangent is tangent. i.e., 1/cot x = tan x.
- The inverse of cotangent is arccot (or) cot-1.
How do You Find the Angle Using cot x Formula?
If in a triangle, we know the adjacent and opposite sides of an angle, then by finding the inverse cotangent function, i.e., cot-1(adjacent/opposite), we can find the angle.
What are the Derivative and Integral of Cot x?
The derivative and the integral of the cotangent function are obtained by using its definition cot x = (cos x)/(sin x).
- The derivative of cot x is -csc2x.
- The integral of cot x is ln |sin x| + C.
visual curriculum