A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
LearnPracticeDownload

Odd Function

The odd functions are functions that return their negative inverse when x is replaced with –x. This means that f(x) is an odd function when f(-x) = -f(x). Some examples of odd functions are trigonometric sine function, tangent function, cosecant function, etc. Let us understand the odd functions and their properties in detail in the following section.

1. What is an Odd Function?
2. General formula of an ODD Function
3. Graphical Representation of Odd Function
4. Properties of Odd Functions
5. FAQs on Odd Functions

What is an Odd Function?

A function is odd if −f(x) = f(−x), for all x. The graph of an odd function will be symmetrical about the origin. For example, f(x) = x3 is odd. That is, the function on one side of x-axis is sign inverted with respect to the other side or graphically, symmetric about the origin.

odd function curve

Odd Function Example

Look at an example of an odd function, a graph of f(x) = x5

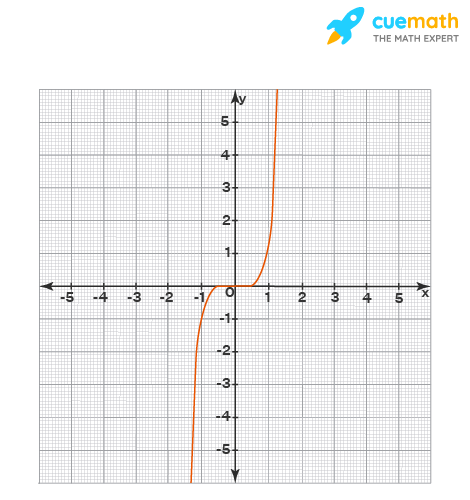
odd function plot

Observe the graph in the 1st and 3rd quadrants. The graph looks symmetrical about the origin. Note that all functions having odd power like are odd functions.

f(x) = x7 is an odd function but f(x) = x3 + 2 is not an odd function. Can you verify with the odd function rule?

General formula of an Odd Function

Algebraically, without looking at a graph, we can determine whether the function is even or odd by finding the formula for the reflections.

f(−x) = −f(x) for all x

Example:

Determine the nature of the function f(x) = 1/x

The function is odd, if f(−x) = −f(x) and even if f(x) = f(−x),

Let us find f(−x) to determine the nature of the function.

f(−x) = 1/-x = −1/x
= −f(x) (∵ f(x) = 1/x)

Since f(−x) = −f(x) the function is odd.

Graphical Representation of Odd Function

Odd Functions are symmetrical about the origin. The function on one side of x-axis is sign inverted with respect to the other side or graphically, symmetric about the origin. Here are a few examples of odd functions, observe the symmetry about the origin.

y = x3

examples of odd function

f(x) = −x is odd

odd function plot example

f(x) = 6sin(x)

odd function 6 sin x curve

Properties of Odd Functions

Like other functions in maths, odd functions have their own properties which can b used to identify the odd function easily. Let us look at few properties.

  • The sum of two odd functions is odd.
  • The difference between two odd functions is odd.
  • The product of two odd functions is even.
  • The quotient of the division of two odd functions is even.
  • The composition of two odd functions is odd.
  • The composition of an even function and an odd function is even.

☛Articles on Odd Function

Given below is the list of topics that are closely connected to the odd function. These topics will also give you a glimpse of how such concepts are covered in Cuemath.

 

Odd Functions Examples

  1. Example 1: Determine algebraically whether the given function f(x) = −3x3 + 2x even, odd, or neither.

    Solution:

    Let us substitute −x into the function f(x) = 3x3 + 2x, and then simplify.

    A function is odd if −f(x) = f(−x)

    Let us find f(-x)

    f(x) = −3x3 + 2x
    f(−x) = -3(−x)3 + 2(−x)
    = −3(−1)3 (x)3 + 2(−x)
    = 3x3 − 2x −−−(1)
    −f(x) = −(−3x3 + 2x)
    = 3x3 − 2x −−−(2)
    from (1) and (2) we can say that f(−x) = −f(x)
    and the given function is an odd function.

    f(x) = −3x3 + 2x is an odd function.

  2. Example 2: Determine the nature of the function f(x) = x3 + 2x.

    Solution: The function is

    • even if f(x) = f(−x)
    • odd if f(−x) = −f(x)

    Let us find f(−x) to determine the nature of the function

    f(−x) = (−x)3 + 2(−x)
    = −x3 − 2x
    = −(x3 + 2x)
    = −f(x)

    f(−x) = −f(x) this is an odd function.

  3. Example 3: Draw the odd function graph for the example 2 i.e., f(x) = x3 + 2x and state why is it an odd function.

    Solution: Let us plot the given function

    graph of an odd function

    • Notice that the graph is symmetric about the origin.
    • For every point (x,y)on the graph, the corresponding point (−x,−y) is also on the graph
    • For example (1,3) is on the graph of f(x) and the corresponding reflection point (−1,−3) is also on the graph.

    Hence the given function f(x) is odd.

View Answer >

go to slidego to slidego to slide

Breakdown tough concepts through simple visuals.
Math will no longer be a tough subject, especially when you understand the concepts through visualizations.

Book a Free Trial Class

FAQs on Odd Function

What are Odd Functions in Calculus?

In calculus an odd function is defined as, −f(x) = f(−x), for all x. The graph of an odd function will be symmetrical about the origin. For example, f(x) = x3 is odd.

What is the Odd Function Equation?

The odd function equation mathematically expressed as −f(x) = f(−x), for all x.

How to Determine if a Function is an Odd Function or Not?

If a function satisfies the following terms it is an odd function:

  • If the value of f(−x) is the same as the value of f(x) for every value of x, the function is even.
  • If the value of f(−x) is NOT the same as the value of f(x) for any value of x, the function is not even.
  • If a function has an even power, the function need not be an even function.

Is Cos x an Odd Function?

The odd function equation mathematically expressed as −f(x) = f(−x), for all x. On substituting the value we have cos(−x) = cos x. Therefore, cos⁡x is NOT an odd function but it is an even function.

How do You Tell if a Graph is for Odd Function, Even, or Neither?

There are certain rules to identify whether the plotted graph is of an odd function or not. The rules are listed below.

  • ODD if it is symmetric about the origin,
  • EVEN if it is symmetric about Y-axis
  • NEITHER if otherwise.

What are the Three Major Properties of an Odd Function?

There are various properties that define an even function. The two major properties are:

  • When we subtract two odd functions the resultant difference is odd.
  • When we multiply two odd functions the resultant product is even.
  • When we add two odd functions the resultant sum is odd.

Is There Any Function that is Neither Odd Function or Even?

A function can be neither even nor odd. Example: x3 - x + 1

Why is Sine an Odd Function?

We know that sin (-x) = -sin (x). The graph of sin(x) is symmetric about origin. So, it is an odd function.

Download FREE Study Materials
Worksheets on Odd Function
Math worksheets and
visual curriculum