A day full of math games & activities. Find one near you.

Increasing and Decreasing Functions

Increasing and decreasing functions are functions in calculus for which the value of f(x) increases and decreases respectively with the increase in the value of x. The derivative of the function f(x) is used to check the behavior of increasing and decreasing functions. The function is said to be increasing if the value of f(x) increases with an increase in the value of x and the function is said to be decreasing if the value of f(x) decreases with an increase in the value of x.

In this article, we will study the concept of increasing and decreasing functions, their properties, graphical representation, and theorems to test for increasing and decreasing functions along with examples for a better understanding.

1.	What are Increasing and Decreasing Functions?
2.	Graphical Representation of Increasing and Decreasing Functions
3.	Rules to Check Increasing and Decreasing Functions
4.	Properties of Increasing and Decreasing Functions
5.	FAQs on Increasing and Decreasing Functions

What are Increasing and Decreasing Functions?

Increasing and decreasing functions are functions whose graphs go upwards and downwards respectively as we move towards the right-hand side of the x-axis. Increasing and decreasing functions are also called non-decreasing and non-increasing functions. Let us go through the formal definition of increasing and decreasing functions to understand their meaning:

Increasing and Decreasing Functions Definition

Increasing Function - A function f(x) is said to be increasing on an interval I if for any two numbers x and y in I such that x < y, we have f(x) ≤ f(y).
Decreasing Function - A function f(x) is said to be decreasing on an interval I if for any two numbers x and y in I such that x < y, we have f(x) ≥ f(y).
Strictly Increasing Function - A function f(x) is said to be strictly increasing on an interval I if for any two numbers x and y in I such that x < y, we have f(x) < f(y).
Strictly Decreasing Function - A function f(x) is said to be strictly decreasing on an interval I if for any two numbers x and y in I such that x < y, we have f(x) > f(y).

Graphical Representation of Increasing and Decreasing Functions

Now, that we know the meaning and definition of increasing and decreasing functions, let us see the graphical representation of increasing and decreasing functions which will help us to understand the behavior of the functions.

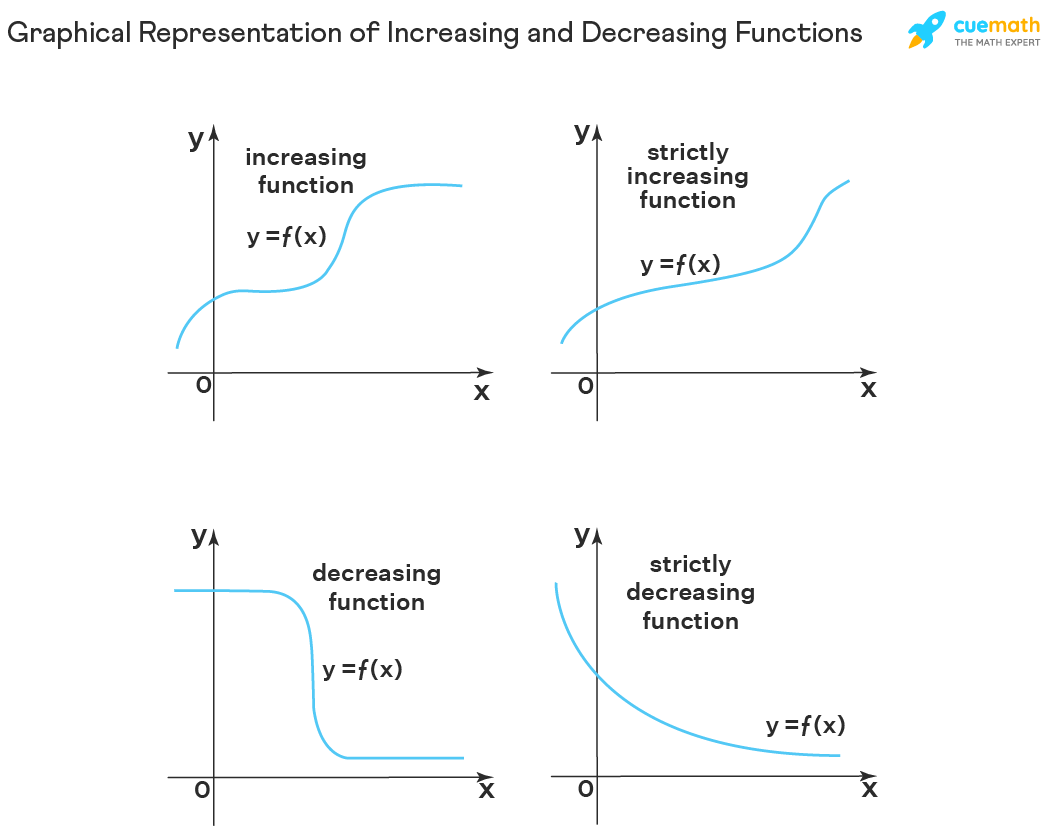
Increasing and Decreasing Functions

The above graphs show the graphical representation of strictly increasing, strictly decreasing, increasing and decreasing functions. As we can see above in the graphs, the increasing function contains both strictly increasing intervals and the intervals where the function is constant. Similarly, a decreasing function consists of intervals where the function is strictly decreasing and where the function is constant.

Rules to Check Increasing and Decreasing Functions

We use the derivative of a function to check if it is an increasing or decreasing function. Suppose a function f(x) is differentiable on an open interval I, then we have

If f'(x) ≥ 0 on I, the function is said to be an increasing function on I.
If f'(x) ≤ 0 on I, the function is said to be a decreasing function on I.

Example: Let us consider an example to understand the concept better. Consider f(x) = x³ defined for all real numbers. The derivative of f(x) = x³ is given by f'(x) = 3x². We know that square of a number is always greater than or equal to 0, therefore we have f'(x) = 3x² ≥ 0 for all x. Hence f(x) = x³ is an increasing function.

Properties of Increasing and Decreasing Functions

Since we know how to check if a function is increasing or decreasing, let us go through the algebraic properties of increasing and decreasing functions:

If the functions f and g are increasing functions on an open interval I, then the sum of the functions f + g is also increasing on this interval.
If the functions f and g are decreasing functions on an open interval I, then the sum of the functions f + g is also decreasing on this interval.
If the function f is an increasing function on an open interval I, then the opposite function -f is decreasing on this interval.
If the function f is a decreasing function on an open interval I, then the opposite function -f is increasing on this interval.
If the function f is an increasing function on an open interval I, then the inverse function 1/f is decreasing on this interval.
If the function f is a decreasing function on an open interval I, then the inverse function 1/f is increasing on this interval.
If the functions f and g are increasing functions on an open interval I and f, g ≥ 0 on I, then the product of the functions fg is also increasing on this interval.
If the functions f and g are decreasing functions on an open interval I and f, g ≥ 0 on I, then the product of the functions fg is also decreasing on this interval.

Important Notes on Increasing and Decreasing Functions

The first derivative of a function is used to check for increasing and decreasing functions.
Increasing and decreasing functions are also called non-decreasing and non-increasing functions.

☛ Related Topics:

Increasing and Decreasing Functions Examples

Example 1: Determine the interval(s) on which f(x) = xe^-x is increasing using the rules of increasing and decreasing functions.

Solution: To determine the interval where f(x) is increasing, let us find the derivative of f(x).

f(x) = xe^-x

f'(x) = e^-x - xe^-x

= e^-x(1 - x)

To determine the critical point, equate f'(x) with 0, that is,

e^-x(1 - x) = 0 ⇒ x = 1 [Because exponential function cannot be equal to 0]
- For x < 1, (1 - x) > 0 ⇒ e^-x(1 - x) > 0 [because exponential is always positive]
- For x > 1, (1 - x) < 0 ⇒ e^-x(1 - x) < 0 [because exponential is always positive]
Hence, we have f'(x) > 0 for x < 1. Therefore, the interval where f(x) = xe^-x is increasing on (-∞, 1).

Answer: f(x) = xe^-x is increasing on (-∞, 1)
Example 2: Use the graph of the derivative function f'(x) to determine the intervals where f(x) is increasing or decreasing.

Solution: We know that for a differentiable function f(x) to be increasing on an interval I, we need to have f'(x) > 0 for all x in I and or a differentiable function f(x) to be decreasing on an interval I, we need to have f'(x) < 0 for all x in I.

As we can see in the image above, the graph of f'(x) > 0 (above x-axis) in the interval (-2, 2) and the graph of f'(x) < 0 (below x-axis) in the intervals (-∞, -2) and (2, ∞). Therefore, the function f(x) is increasing in (-2, 2) and decreasing in (-∞, -2) ∪ (2, ∞).

Answer: Intervals where f(x) is increasing is (-2, 2) and where f(x) is decreasing is (-∞, -2) ∪ (2, ∞).

go to slide go to slide

Great learning in high school using simple cues

Indulging in rote learning, you are likely to forget concepts. With Cuemath, you will learn visually and be surprised by the outcomes.

Book a Free Trial Class

Increasing and Decreasing Functions Problems

go to slide go to slide

FAQs on Increasing and Decreasing Functions

What are Increasing and Decreasing Functions in Calculus?

Increasing and decreasing functions are defined as:

Increasing Function - A function f(x) is said to be increasing on an interval I if for any two numbers x and y in I such that x < y, we have f(x) ≤ f(y).
Decreasing Function - A function f(x) is said to be decreasing on an interval I if for any two numbers x and y in I such that x < y, we have f(x) ≥ f(y).

How Do you Know If a Function is Increasing or Decreasing?

Suppose a function f(x) is differentiable on an open interval I, then we have

If f'(x) ≥ 0 on I, the function is said to be an increasing function on I.
If f'(x) ≤ 0 on I, the function is said to be a decreasing function on I.

Which Function is Neither Increasing Nor Decreasing?

A constant function is neither increasing nor decreasing as the graph of a constant function is a straight line parallel to the x-axis and its derivative is always 0.

How to Find where Functions are Increasing and Decreasing Functions?

Functions can be identified as increasing and decreasing functions using differentiation. We can find the derivative of the function and determine its critical point. Around the critical point, we can check the sign of the derivative and determine if it is increasing or decreasing.

How to Find Intervals of Increasing and Decreasing Functions?

Intervals of increasing and decreasing functions can be calculated using differentiation. We can find the derivative of the function and determine its critical point. Around the critical point, we can check the sign of the derivative and determine if it is increasing or decreasing. Suppose a function f(x) is differentiable on an open interval I. If f'(x) ≥ 0 on I, the function is said to be an increasing function on I. If f'(x) ≤ 0 on I, the function is said to be a decreasing function on I.

How to Identify Increasing and Decreasing Functions Through Graph?

As move towards, the right-hand side of the x-axis (increase in value of x), if the graph of f(x) goes upwards or remains constant, then f(x) is increasing and if the graph of f(x) goes downwards or remains constant, then f(x) is decreasing.

Math worksheets and
visual curriculum