Trigonometric Ratios
Trigonometric ratios are the ratios of the length of sides of a triangle. These ratios in trigonometry relate the ratio of sides of a right triangle to the respective angle. The basic trigonometric ratios are sin, cos, and tan, namely sine, cosine, and tangent ratios. The other important trig ratios, cosec, sec, and cot, can be derived using the sin, cos, and tan respectively.
The word "Trigonometry" originated from the words, "Trigonon" which means "triangle" and "Metron" which means "to measure". It is a branch of mathematics that deals with the relation between the angles and sides of a right-angled triangle. In fact, trigonometry is one of the most ancient subjects which is studied by scholars all over the world. Let us understand the trigonometric ratios in detail in the following sections.
| 1. | What are Trigonometric Ratios? |
| 2. | Trigonometric Ratios Formulas |
| 3. | Trigonometric Ratios Table |
| 4. | Trigonometric Ratios Identities |
| 5. | FAQs on Trigonometric Ratios |
What are Trigonometric Ratios?
In trigonometry, there are six trigonometric ratios, namely, sine, cosine, tangent, secant, cosecant, and cotangent. These ratios are written as sin, cos, tan, sec, cosec(or csc), and cot in short. Let us have a look at the right-angled triangle shown below. Trigonometric ratios can be used to determine the ratios of any two sides out of a total of three sides of a right-angled triangle in terms of the respective angles.
The values of these trigonometric ratios can be calculated using the measure of an acute angle, θ in the right-angled triangle given below. This implies that the value of the ratio of any two sides of the triangle here depends on angle C. We can alternatively find the values of these trig ratios for angle A. Also, only the base and perpendicular will interchange for the given right triangle in that case.
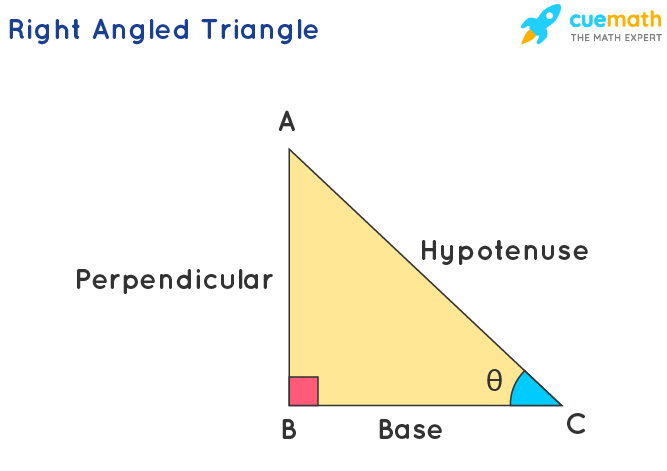
These six trigonometric ratios can be defined as,
Sine: The sine ratio for any given angle is defined as the ratio of the perpendicular to the hypotenuse. In the given triangle, sine of angle θ can be given as, sin θ = AB/AC.
Cosine: The cosine ratio for any given angle is defined as the ratio of the base to the hypotenuse. In the given triangle, cosine of angle θ can be given as, cos θ = BC/AC.
Tangent: The tangent ratio for any given angle is defined as the ratio of the perpendicular to the base. In the given triangle, the tangent of angle θ can be given as, tan θ = AB/BC.
Cosecant: The cosecant ratio for any given angle is defined as the ratio of the hypotenuse to the perpendicular. In the given triangle, cosecant of angle θ can be given as, cosec θ = AC/AB.
Secant: The secant ratio for any given angle is defined as the ratio of the hypotenuse to the base. In the given triangle, secant of angle θ can be given as, sec θ = AC/BC.
Cotangent: The cotangent ratio for any given angle is defined as the ratio of the base to the perpendicular. In the given triangle, cotangent of angle θ can be given as, cot θ = BC/AB.
Let us understand these and more trigonometric ratio formulas in detail in the next section.
Trigonometric Ratios Formulas
Trigonometric ratios can be calculated by taking the ratio of any two sides of the right-angled triangle. We can evaluate the third side using the Pythagoras theorem, given the measure of the other two sides. We can use the abbreviated form of trigonometric ratios to compare the length of any two sides with the angle in the base. The angle θ is an acute angle (θ < 90º) and in general is measured with reference to the positive x-axis, in the anticlockwise direction. The basic trigonometric ratios formulas are given below,
- sin θ = Perpendicular/Hypotenuse
- cos θ = Base/Hypotenuse
- tan θ = Perpendicular/Base
- sec θ = Hypotenuse/Base
- cosec θ = Hypotenuse/Perpendicular
- cot θ = Base/Perpendicular
Now, let us observe the reciprocal trigonometric ratio formulas of the above-mentioned trigonometric ratios. As we observe, we notice that sin θ is a reciprocal of cosec θ, cos θ is a reciprocal of sec θ, tan θ is a reciprocal of cot θ, and vice-versa. So, the new set of formulas for trigonometric ratios is:
- sin θ = 1/cosec θ
- cos θ = 1/sec θ
- tan θ = 1/cot θ
- cosec θ = 1/sin θ
- sec θ = 1/cos θ
- cot θ = 1/tan θ
Trigonometric Ratios Table
In the trigonometric ratios table, we use the values of trigonometric ratios for standard angles 0°, 30°, 45°, 60°, and 90º. It is easy to predict the values of the table and to use the table as a reference to calculate values of trigonometric ratios for various other angles, using the trigonometric ratio formulas for existing patterns within trigonometric ratios and even between angles. Now, we will summarize the value of trigonometric ratios for specific angles in the table below:
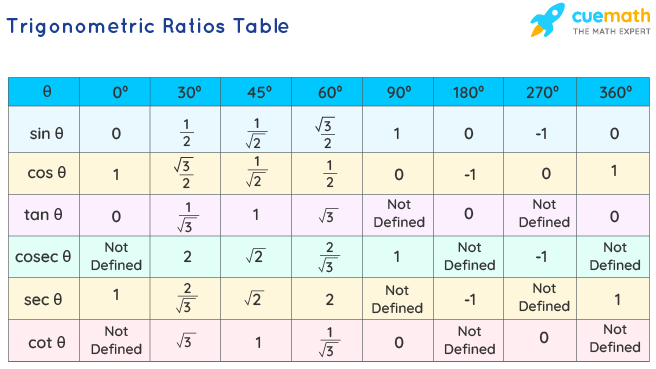
Trigonometric Ratios Identities
There are many trigonometric ratios identities that we use to make our calculations easier and simpler. These include identities of complementary angles, supplementary angles, Pythagorean identities, and sum, difference, product identities.
Trigonometric Ratios of Complementary Angles Identities
The complementary angles are a pair of two angles such that their sum is equal to 90°. The complement of an angle θ is (90° - θ). The trigonometric ratios of complementary angles are:
- sin (90°- θ) = cos θ
- cos (90°- θ) = sin θ
- cosec (90°- θ) = sec θ
- sec (90°- θ) = cosec θ
- tan (90°- θ) = cot θ
- cot (90°- θ) = tan θ
Pythagorean Triogometric Ratios Identities
The Pythagorean trigonometric ratios identities in trigonometry are derived from the Pythagoras theorem. Applying Pythagoras theorem to the right-angled triangle below, we get:
Opposite2 + Adjacent2 = Hypotenuse2
Dividing both sides by Hypotenuse2
Opposite2/Hypotenuse2 + Adjacent2/Hypotenuse2 = Hypotenuse2/Hypotenuse2
- sin2θ + cos2θ = 1
This is one of the important Pythagorean identities. In the same way, we can derive two other Pythagorean trigonometric ratios identities:
- sin2θ + cos2θ = 1
- 1 + tan2θ = sec2θ
- 1 + cot2θ = cosec2θ
Sum, Difference, Product Trigonometric Ratios Identities
The sum, difference, and product trigonometric ratios identities include the formulas of sin(A+B), sin(A-B), cos(A+B), cos(A-B), etc.
- sin (A + B) = sin A cos B + cos A sin B
- sin (A - B) = sin A cos B - cos A sin B
- cos (A + B) = cos A cos B - sin A sin B
- cos (A - B) = cos A cos B + sin A sin B
- tan (A + B) = (tan A + tan B)/ (1 - tan A tan B)
- tan (A - B) = (tan A - tan B)/ (1 + tan A tan B)
- cot (A + B) = (cot A cot B - 1)/(cot B - cot A)
- cot (A - B) = (cot A cot B + 1)/(cot B - cot A)
- 2 sin A⋅cos B = sin(A + B) + sin(A - B)
- 2 cos A⋅cos B = cos(A + B) + cos(A - B)
- 2 sin A⋅sin B = cos(A - B) - cos(A + B)
Half, Double, and Triple-Angles Trigonometric Ratios Identities
Double Angle Trigonometric Ratios Identities
The double angle trigonometric identities can be obtained by using the sum and difference formulas.
For example, from the above formula sin (A+B) = sin A cos B + cos A sin B
Substitute A = B = θ on both sides here, we get:
sin (θ + θ) = sinθ cosθ + cosθ sinθ
sin 2θ = 2 sinθ cosθ
In the same way, we can derive the other double angle identities.
- sin 2θ = 2 sinθ cosθ
- cos 2θ = cos2θ - sin2θ
cos 2θ = 2 cos2θ - 1
cos 2θ = 1 - 2 sin2θ
cos 2θ = (1 - tan2 θ)/(1 + tan2 θ) - tan 2θ = (2 tanθ)/ (1 - tan2θ)
- sec 2θ = sec2 θ/(2-sec2 θ)
- cosec 2θ = (sec θ. cosec θ)/2
- cot 2θ = (cot θ - tan θ)/2
Half Angle Trigonometric Ratios Identities
Using one of the above double angle formulas,
cos 2θ = 1 - 2 sin2θ
2 sin2θ = 1- cos 2θ
sin2θ = (1 - cos 2θ)/(2)
sin θ = ±√[(1 - cos 2θ)/2]
Replacing θ by θ/2 on both sides,
sin (θ/2) = ±√[(1 - cos θ)/2]
This is the half-angle formula of sine.
In the same way, we can derive the other half-angle formulas.
- sin (θ/2) =±√[(1 - cos θ)/2]
- cos (θ/2) = ±√[(1 + cos θ)/2]
- tan (θ/2) = ±√[(1 - cos θ)(1 + cosθ)]
Triple Angle Trigonometric Ratios Identities
- sin 3θ = 3sin θ - 4sin3θ
- cos 3θ = 4cos3θ - 3cos θ
- tan 3θ = (3tanθ - tan3θ)/(1 - 3tan2θ)
Related Topics:
Important Notes on Trigonometric Ratios:
- The values of trigonometric ratios do not change with the change in the side lengths of the triangle if the angle remains the same.
- All trigonometric functions are periodic in nature.
- Trigonometric ratios are used to find the missing sides or angles in a triangle.
Examples on Trigonometric Ratios
-
Example 1: In a right-angled triangle ABC, right-angled at B, hypotenuse AC = 10 units, base BC = 8 units and perpendicular AB = 6 units and if ∠ACB = θ, then find the trigonometric ratios tan θ, sin θ, and cos θ.
Solution:
We know,
sin θ = perpendicular/hypotenusecos θ = base/hypotenuse
tan θ = perpendicular/base
⇒ sin θ = 6/10 = 3/5
⇒ cos θ = 8/10 = 4/5
⇒ tan θ = 6/8 = 3/4
Answer: sin θ, cos θ, and tan θ for the given triangle are 3/5, 4/5, and 3/4 respectively.
-
Example 2: A building is at a distance of 210 feet from point A on the ground. Find the height of the building if tan θ = 4/3?
Solution: The triangle formed is a right-angled triangle. Now apply the trigonometric ratio of tanθ to calculate the height of the building.
tan θ = Perpendicular/Base
4/3 = Height/210 ft
Height = (4 × 210/3) = 280 ft
Answer: The height of the building is 280 ft.
-
Example 3: The triangle is right-angled at C with AB = 29 units and AC = 20 units. Can you verify the trigonometric ratios identity cos2θ + sin2θ = 1 using these values?
Solution: We will find BC using the Pythagorean theorem,
BC = √(AB2 - AC2)
= √(292 - 202)
= √8412 - 4002)
= √441
= 21
Now let's determine the values of sinθ and cosθ
sinθ = AC/AB = 20/29
cosθ = BC/AB = 21/29
Now let's verify the identity.
cos2θ + sin2θ = (21/29)2 + (20/29)2 = (400 + 441)/841 = 1
Answer: Hence, the trigonometric ratios identity is verified.

FAQs on Trigonometric Ratios
How to Find Trigonometric Ratios?
Trigonometric Ratios can be calculated either by using the given acute angle or determining the ratios of the sides of the right-angled triangle. The trigonometric ratios formulas to be used are:
- sin θ = Perpendicular/Hypotenuse
- cos θ = Base/Hypotenuse
- tan θ = Perpendicular/Base
- sec θ = Hypotenuse/Base
- cosec θ = Hypotenuse/Perpendicular
- cot θ = Base/Perpendicular
What are the Six Trigonometric Ratios?
The main six trigonometric ratios are sine, cosine, tangent, cosecant, secant, and cotangent. The trigonometric ratios can be calculated using the formulas given in the article.
What are the Applications of Trigonometric Ratios?
There are various applications of trigonometric ratios such as:
- Sine and cosine are used to represent sound waves.
- Some trigonometric ratios are used in the field of architecture, constructing buildings, etc.
- They are used in creating maps.
What are Trigonometric Ratios of Specific Angles?
Trigonometric ratios can be determined for different angles. But for convenience of calculations, we memorize the trigonometric ratios of some specific angles like 0°, 30°, 45°, 60°, 90°. Refer to the trigonometric ratios table for the values of the ratios at these angles.
What are Trigonometric Ratios of Complementary Angles?
Complementary angles are two angles whose sum is 90°. Formulas for trigonometric ratios of complementary angles are:
- sin (90°- θ) = cos θ
- cos (90°- θ) = sin θ
- cosec (90°- θ) = sec θ
- sec (90°- θ) = cosec θ
- tan (90°- θ) = cot θ
- cot (90°- θ) = tan θ
What is the Relationship Between Sin, Cos, and Tan Trigonometric Ratios?
We know, that sin can be given as perpendicular/hypotenuse, cos as base/hypotenuse, and tan as perpendicular/base. The relationship between the trigonometric ratios sin, cos, and tan can therefore be given as, tan θ = sin θ/cos θ.
visual curriculum