A day full of math games & activities. Find one near you.

Integration by Substitution

Integration by substitution is an important method of integration, which is used when a function to be integrated, is either a complex function or if the direct integration of the function is not feasible. The integral of a function is simplified by this method of integration by substitution, by reducing the given function into a simplified function.

Let us learn the process of integration by substitutions, check some of the important substitutions, and also check the solved examples.

1.	What Is Integration by Substitution?
2.	Steps to Integration by Substitution
3.	Important Substitutions in Integration by Substitution
4.	Examples on Integration by Substitution
5.	Practice Questions
6.	FAQs on Integration by Substitution

What Is Integration by Substitution?

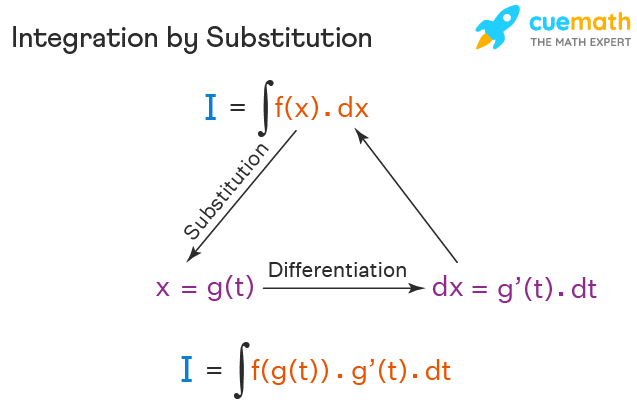
Integration by substitution is used when the integration of the given function cannot be obtained directly, as the given algebraic function is not in the standard form. Further, the given function can be reduced to the standard form by appropriate substitution. Let us consider the indefinite integral of a function f(x), \(\int f(x).dx\). Here this integral can be transformed to another form by replacing x with g(t) and by substituting x = g(t).

I = \(\int f(x).dx\)

x = g(t) such that dx/dt = g'(t)

dx = g'(t).dt

I =\(\int f(x).dx = \int f(g(t)).g'(t).dt\)

Integration by Substitution

Steps to Integration by Substitution

The following are the steps that are helpful in performing this method of integration by substitution.

Step - 1: Choose a new variable t for the given function to be reduced.

Step - 2: Determine the value of dx, of the given integral, where f(x) is integrated with respect to x.

Step - 3: Make the required substitution in the function f(x), and the new value dx.

Step - 4: Integrate the function obtained after substitution

Step - 5: Substitute back the initial variable x to obtain the final answer.

Important Substituions in Integration by Substitution

The following are some of the important substitutions which are helpful in simplifying the given expression and easily performing the integration process. Let us check the following specific substitutions for integration by substitution.

For the integral function \(f(\sqrt{a^2 - x^2})\) we use x = aSinθ or x = aCosθ.
For the integral of the function \(f(\sqrt {x^2 - a^2})\) we use x = a Secθ or x = aCosecθ.
For the integral of the function \(f(x^2 + a^2)\). \(f(\sqrt{x^2 + a^2})\) we use x = aTanθ, or x = aCotθ.
For the integral of the functions \(f(\sqrt {\dfrac{a - x}{a + x}})\) , \(f(\sqrt {\dfrac{a + x}{a - x}})\), we use x = a Cos2θ.

Related Topics

The following topics help in a better understanding of this concept of integration by substitution.

Examples on Integration by Substitution

Example 1: Find the integral of \(\dfrac {e^{Tan^{-1}x}}{1 + x^2}\).

Solution:

The given expression for integration is \(\int \dfrac {e^{Tan^{-1}x}}{1 + x^2}.dx\)

Here let us take \(Tan^{-1}x = t\), and we can differentiate it further.

\(\dfrac{d}{dx}.Tan^{-1}x = \dfrac{d}{dx}.t\)

\(\dfrac{1}{1 + x^2} = \dfrac{dt}{dx}\)

\(dx =(1 + x^2).dt\)

Let us now substitute the 't' value and dx value in the given expression for integration.

\(\int \dfrac {e^{Tan^{-1}x}}{1 + x^2}.dx = \int \dfrac{e^t}{1+ x^2}.(1 + x^2).dt\)

= \(\int e^t.dt\)

= \(e^t + C\)

= \(e^{Tan^{-1}x} + C\)

Therefore, the integration of \(\dfrac {e^{Tan^{-1}x}}{1 + x^2}\) is \(e^{Tan^{-1}x} + C\).
Example 2: Find the integral of \(2xSec^2(x^2 + 1)\).

Solution:

The given expression for integration is \(\int 2xSec^2(x^2 + 1).dx\).

Here we substitute \(x^2 + 1 = t\) and differentiate it further.

\(\dfrac{d}{dx}.(x^2 + 1) = \dfrac{d}{dx}.t\)

2x = dt/dx

dx = dt/2x

Let us now substitute t and dx value in the above expression of integration.

\(\int.2xSec^2(x^2 + 1).dx = \int 2xSec^2t.\dfrac{dt}{2x}\)

=\(\int Sec^2t.dt\)

= Tant + c

= Tan(x² + 1) + C

Therefore the integration of \(\int 2xSec^2(x^2 + 1).dx\) is Tan(x² + 1) + C.

go to slide go to slide

Have questions on basic mathematical concepts?

Become a problem-solving champ using logic, not rules. Learn the why behind math with our certified experts

Book a Free Trial Class

Practice Questions on Integration by Substitution

go to slide go to slide

FAQs on Integration by Substitution

What Is Integration by Substitution?

Integration by substitution is an important method of integration, which is used when a function to be integrated, is either a complex function or if the direct integration of the function is not feasible.

How Do You Integrate by Substitution?

Integration by substitution can be performed through a set of sequential steps. First, choose a new variable for the part of the function to be substituted. Secondly, determine the value of differentiation of x, ie dx from this new variable substitution. The third steps involve the process of integration involving this new variable. Finally, substitute back the initial variable to obtain the final answer.

How Do You Know When To Use Integration by Substitution?

The process of integration by substitution is used if the given function to be integrated has one of the following three characteristics.

The given function has a sub-function.
The function to be integrated is a complex number-based function.
The direct integration of the function is not possible.

What Is the Formula For Integration by Substitution?

There is no defined formula for integration by substitution. Based on the given function, the part of the function which is to be substituted is substituted with a new variable.

How Do You Use Integration By Substitution for Trigonometric Formulas?

The integration by substitution is used for trigonometric functions, similar to any other function. Here the trigonometric function is replaced with a new variable, to transform it into an algebraic expression, which is easy to integrate.

Math worksheets and
visual curriculum