Polynomial Expressions

The word polynomial is made of two words, "poly" and "nomial", meaning many terms. It is used in math for representing expressions. Thus, a polynomial expression is a sentence with a minimum of two numbers and at least one math operation in it.

A polynomial is made up of terms and each term has a coefficient, while an expression is a sentence with a minimum of two numbers and at least one math operation in it. The expressions which satisfy the criterion of a polynomial are polynomial expressions. Let's see the following examples to check if they are polynomial expressions or not.

In the two cases discussed above, the expression x² + 3√x + 1 is not a polynomial expression because the variable has a fractional exponent, i.e., 1/2 which is a non-integer value; while for the second expression x² + √3 x + 1, the fractional power 1/2 is on the constant which is 3 in this case, hence it is a polynomial expression.

Standard Form of Polynomial Expressions

The standard form of any polynomial expression is given when the terms of expression are ordered from the highest degree to the lowest degree. The polynomial standard form can be written as: \(a_{n}x^{n}+a_{n-1}x^{n-1}+.......+a_{2}x^2+a_{1}x+a_{0}\). For example, ax² + bx + c.

There are three types of polynomials based on the number of terms that they have:

• Monomial
• Binomial
• Trinomial

Monomial

A monomial consists of only one term with a condition that this term should be non-zero. Examples: 6x, 7x³, 2ab

Binomial 

A binomial is a polynomial that consists of two terms. It is written as the sum or difference of two or more monomials. Examples: 2x⁴ + 8x, 8y³ + 3x, xy² + 3y

Trinomial 

A trinomial is a polynomial that consists of three terms. Examples: 3x² + 4x + 10, 5y⁴ + 3x⁴ + 2x², 7y² + 3y + 17

For a Single Variable Polynomial

We find the degree of a polynomial expression using the following steps:

• Step 1: Combine the like terms of the polynomial expression.
• Step 2: Write the polynomial expression in the standard form.
• Step 3: Check and select the highest exponent.

The highest exponent of the expression gives the degree of the polynomial. Let's consider the polynomial expression, 5x³ + 4x² - x⁴ - 2x³ - 5x² + x⁴. In this case, the expression can be simplified as, 3x³ - x². Here, the highest exponent corresponding to the polynomial expression is 3. Hence, the degree of polynomial expression is 3. Observe the following expression.

The above expression shows:

• Three terms: 8x², 5x and 6
• The variables: x² and x
• The coefficients of the variables: 8 and 5
• Constant: 6
• Degree of the polynomial: 2

For a Multivariable Polynomial

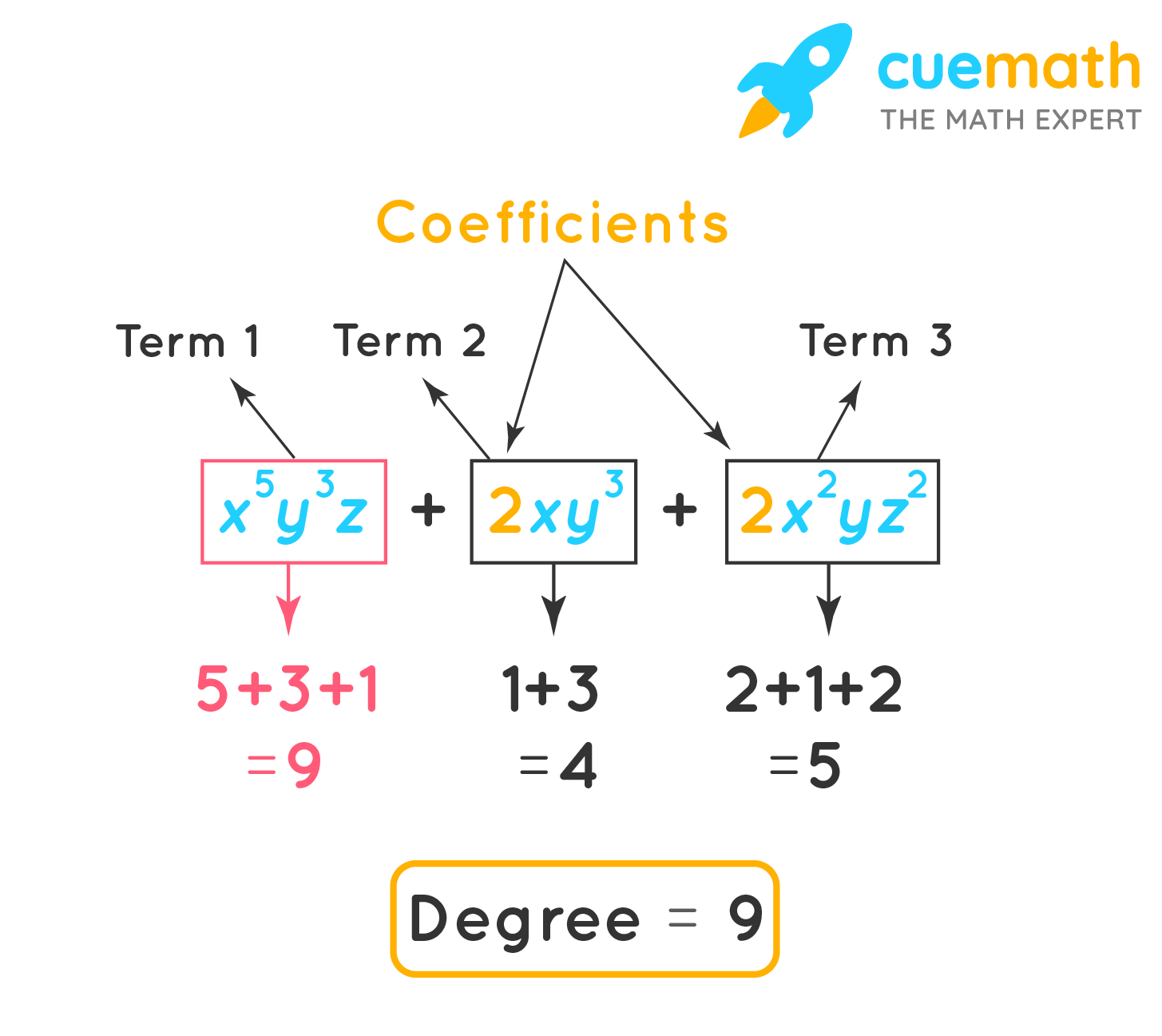
If we take a polynomial expression with two variables, say x and y, x³ + 3x²y⁴ + 4y² + 6. We follow the above steps, with an additional step of adding the powers of different variables in the given terms. and thus the degree of the polynomial is 6. This is because, in 3x²y⁴, the exponent values of x and y are 2 and 4, respectively. When we add these, we get 6. Hence, the degree of the multivariable polynomial expression is 6. Observe the following polynomial which shows how its degree is considered to be 9.

We can simplify polynomial expressions in the following ways:

By combining like terms

The terms having the same variables are combined using arithmetic operations so that the calculation gets easier. For example, let us simplify the polynomial expression: 5x⁵ + 7x³ + 8x + 9x³ - 4x⁴ - 10x - 3x⁵. We combine the like terms to get, 5x⁵ - 3x⁵ - 4x⁴ + 7x³ + 9x³ + 8x - 10x . On simplifying we get, 2x⁵ - 4x⁴ + 16x³ - 2x 

By using the FOIL technique

The FOIL (First, Outer, Inner, Last) technique is used for the arithmetic operation of multiplication. Each step uses the distributive property. 'First' means multiply the terms which come first in each binomial. Then, 'outer' means multiply the outermost terms in the product, followed by the 'inner' terms, and then the 'last' terms are multiplied. For example, to simplify the given polynomial expression, we use the FOIL technique, (x - 4)(x + 3). The expression can be rewritten as, x (x + 3) - 4 (x + 3). On multiplying the outer terms we get, x² + 3x - 4x - 12. This expression can be reduced to x² - x - 12.

Tips and Tricks

• Positive powers associated with a variable are mandatory in any polynomial, thereby making them one of the important parts of a polynomial.
• Any expression having a non-integer exponent of the variable is not a polynomial. For example, √x which has a fractional exponent.
• A polynomial expression should not have any square roots of variables, any fractional or negative powers on the variables, and no variables should be there in the denominators of any fractions.

Important Notes

• A polynomial with degree 1 is known as a linear polynomial. For example, 2x + 3.
• A polynomial whose degree is 2 is known as a quadratic polynomial. For example, x² + 4x + 4.
• A polynomial with degree 3 is known as a cubic polynomial. For example, x³ + 3x² + 3x + 1.

Topics Related to Polynomial Expressions

• Variable Expressions
• Quadratic Expressions
• nth-degree Polynomial
• Long Division of Polynomials
• Factoring Polynomials

FAQs on Polynomial Expressions

What Is a Polynomial Expression?

Any expression which consists of variables, constants and exponents, and is combined using mathematical operators like addition, subtraction, multiplication and division is a polynomial expression. Polynomial expressions can be classified as monomials, binomials and trinomials according to the number of terms present in the expression.

How Do you Know If an Expression Is a Polynomial?

1. If the expression has a non-integer exponent of the variable.
2. If the expression has any variable in the denominator.
If an expression has the above-mentioned features, it will not be a polynomial expression. For example x² + 2x + 2 is a polynomial, but √x + 2  is not a polynomial.

What Are the 3 Types of Polynomials?

The three types of polynomials are:

• Monomials
• Binomials
• Trinomials

What Is the Difference Between A Polynomial and An Equation?

The difference between a polynomial and an equation is explained as follows:

• A polynomial is an expression that consists of coefficients, variables, constants, operators, and non-negative integers as exponents.
• An equation is a mathematical statement characterized by an 'equal to' symbol (=) between two algebraic expressions, having equal values.

What Is a Zero Polynomial?

A zero polynomial is a polynomial with the degree as 0. It is also called a constant polynomial. 

What Is an Example of a Zero Polynomial?

The example of a zero polynomial is 3 because its degree is zero.

What Are the Terms in a Polynomial?

The terms of polynomials are the parts of the expression that are separated by “+” or “-” signs. For example, in a polynomial, say, 3x² + 2x + 4, there are 3 terms: 3x² , 2x and 4.

How Do you Solve Polynomial Expressions?

The polynomial expressions are solved by:

• Combining like terms (monomials having the same variables using arithmetic operations).
• Using the FOIL (First, Outer, Inner, Last) technique which is used for the arithmetic operation of multiplication.

What Is the Difference Between Zero Polynomial and Zero of a Polynomial?

A zero polynomial is a polynomial with the degree as 0, whereas, zero of a polynomial is the value (or values) of the variable for which the entire polynomial may result in zero.

What Is a Standard Form of a Polynomial?

A polynomial is written in its standard form when its term with the highest degree is first, its term of 2nd highest is 2nd, and so on. It is given as \(a_{n}x^{n}+a_{n-1}x^{n-1}+.......+a_{2}x^2+a_{1}x + a_{0}\). For example, ax³ + bx² + cx + d.