Order of Operations
The order of operations is a set of rules that is to be followed in a particular sequence while solving an expression. In mathematics with the word operations we mean, the process of evaluating any mathematical expression, involving arithmetic operations such as division, multiplication, addition, and subtraction. Let us learn in detail about the order of operations rules and how well we can remember the rules using short tricks.
| 1. | What is the Order of Operations? |
| 2. | Order of Operations Rules |
| 3. | PEMDAS vs BODMAS |
| 4. | How to Use Order of Operations? |
| 5. | Ways to Remember |
| 6. | Real-Life Applications |
| 7. | FAQs on Order of Operations |
What is the Order of Operations?
The order of Operations is the rule in math that states we evaluate the parentheses/brackets first, the exponents/the orders second, division or multiplication third (from left to right, whichever comes first), and the addition or subtraction at the last (from left to right, whichever comes first). In math, there might be several operations to be done while evaluating an expression, and simplification at the end yields different results. However, we can only have one correct answer for any sort of expression. To identify the correct answer we simplify any given mathematical expression using a certain set of rules. These rules revolve around all the basic operators used in maths. Operators such as addition (+), subtraction (-), division (÷), and multiplication (×). Look at the given image to get a glimpse of how the order of operations exactly looks like.
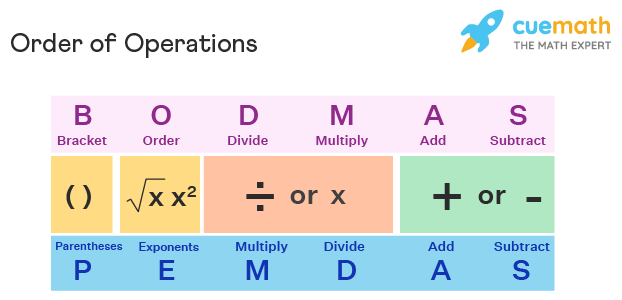
Order of Operations Definition
As we discussed above Order of operations can be defined as, a set of basic rules of precedence we use while solving any mathematical expression, involving multiple operations. When a subexpression appears between two operators, the operator that comes first according to the list given below should be applied first. The order of operations, rules are expressed here:
- Brackets ( ), { }, [ ]
- Exponents
- Division (÷) and Multiplication (×)
- Addition (+) and Subtraction (-)
The above-mentioned set of rules always varies according to the respective given mathematical expressions.
Order of Operations Rules
While performing any sort of an operation on the respective numbers present in the expression we will follow the given basic rules in the particular sequence.
Order of Operations Rule 1: Observe the expression. The first rule is to solve the numbers present inside the parentheses or brackets. We solve inside to out grouping operations. Note the pattern of brackets present in the expression, there is a particular order to solve the parentheses, i.e., [ { ( ) } ]. First, solve the round brackets ( ) → curly brackets { } → box brackets [ ]. Inside the parantheses the order of operations are to be followed.
Order of Operations Rule 2: After solving the numbers in the parentheses, look for any term present in the form of exponents and solve it.
Order of Operations Rule 3: Now we are left with the basic four operators. Look for the numbers with the operation of multiplication or division, solve them from left to right.
Order of Operations Rule 4: Lastly, look for the terms with addition or subtraction and solve them from left to right.
These rules have a specific acronym name. We call them PEMDAS or BODMAS. Let us learn now what exactly PEMDAS or BODMAS is.
Order of Operations - PEMDAS vs BODMAS
The PEMDAS or BODMAS is the two different acronym names given to learn the rules. These two names state the order in which the operations in an expression should be followed. Here is the detailed term for each letter used in the mentioned acronyms. First, we will discuss the PEMDAS.
Order of Operations PEMDAS
- P stands for Parentheses ( ), { }, [ ]
- E stands for Exponents (a2) (For example, here, a is a number with exponent 2)
- M stands for Multiplication (×)
- D stands for Division (÷)
- A stands for Addition (+)
- S stands for Subtraction (-)
Order of Operations BODMAS
- B stands for Brackets ( ), { }, [ ]
- O stands for Order
- D stands for Division (÷)
- M stands for Multiplication (×)
- A stands for Addition (+)
- S stands for Subtraction (-)
With the help of the above denotations, we can easily solve the mathematical expressions and get the correct answer.
How to Use Order of Operations?
Let us look at the different examples mentioned below to understand the accuracy of the rules used in order of operations.
1) For solving parentheses in order of operations:
Expression: 4 × (5 + 2)
Solution: 4 × (7) = 28 (Correct (✔). This is a correct way to solve the parentheses)
Let us look at another approach for the same expression.
4 × (5 + 2) = 20 + 2 = 22 (Incorrect (✘). This is an incorrect way to solve the parentheses)
2) For solving exponents in order of operations
Expression: 4 × (52)
Solution: 4 × (25) = 100 (Correct (✔). This is a correct way to solve the exponents)
Let us look at another approach for the same expression.
4 × (52) = 202 = 400 ((Incorrect (✘). This is an incorrect way to solve the exponents)
3) For multiplication or division and addition or subtraction
Expression: 3 + 5 × 2
Solution: 3 + 5 × 2 = 3 + 10 = 13 (Correct (✔). This is a correct way.)
Let us look at another approach for the same expression.
3 + 5 × 2 = 8 × 2 = 16 (Incorrect (✘). This is an incorrect way.)
Expression: 3 - 6 ÷ 2
Solution: 3 - 6 ÷ 2 = 3 - 3 = 0 (Correct (✔). This is a correct way.)
Let us look at another approach for the same expression.
3 - 6 ÷ 2 = (-3) ÷ 2 = -3/2 (Incorrect (✘). This is an incorrect way.)
Always remember while following the rules of order of operations do multiplication or division before addition or subtraction
Ways to Remember Order of Operations
We just read about the two different words PEMDAS and BODMAS. This is the best way to remember the order of operations. PEMDAS can be remembered by the phrase "Please Excuse My Dear Aunt Sally". In the order of operations, it means "Parentheses, Exponents, Multiplication and Division, and Addition and Subtraction". Here multiplication and division, addition and subtraction are together. Similarly, we can remember the order of operations with the word BODMAS (Brackets, Orders, Division, Multiplication, Addition, and Subtraction.).
The easiest way to learn the order of operation is to perform the given steps:
- Start simplifying terms within the brackets first
- Solve the exponential terms.
- Perform division or multiplication.
- Perform addition or subtraction.
Note: While performing the order of operations on any given expression, we must observe the pattern of operators.
Real-Life Applications of Order of Operations
A lot of activities in our life require some sort of order of operation to perform it well. Let us take an everyday problem. Suppose you went to purchase five pepperoni pizzas that cost $20 each, and you want to split the total cost among 5 people evenly. To find out how much each person needs to pay let's use the order of operations here.
Total number of people = 5
Total number of pizzas = 5
Cost of one pizza = $20
Let us frame an expression using PEMDAS:
Expression: (20 + 20 + 20 + 20 + 20) ÷ 5 or (5 × 20) ÷ 5
Solution: According to PEMDAS or BODMAS we will first solve the parentheses.
(100) ÷ 5 = 20
According to the order of operations, each person needs to pay $20.
Similar to the above-mentioned problem, we have many day-to-day real-life instances where we use order of operations to deal with our problems.
☛Related Articles on Order of Operations
Check out the interesting articles below and learn more about the topic Order of Operations and its applications in detail.
FAQs on Order of Operations
What is the Order of Operations in Math?
The order of operation in math is a set of rules revolving around 4 major operators. According to the order of operations, there is a particular sequence which we need to follow on each operator while solving the given mathematical expression.
How to Solve Order of Operations?
To solve the order of operations first observe the expression and note what pattern it exactly follows. Now start using either PEMDAS or BODMAS to solve the given expression. As per the rules of order of operations do look for parentheses first, then exponents, then move towards multiplication or division and addition or subtraction from left to right.
How to Do Order of Operations with Integers?
We know that integers are positive numbers and negative numbers. We can easily perform the order of operations with integers by following the given steps:
- Look for the integers present inside the parentheses or brackets and solve them.
- After solving the integers in the parentheses, look for any integer term present in the form of exponents and solve it.
- Now we are left with the basic four operators to be performed on integers. Look for the integers with the operation of multiplication or division and solve them from the left-hand side to the right-hand side.
- Lastly, look for the integers with addition or subtraction and solve them.
- In the case of integers, we need to make sure we are properly multiplying the signs. Such that, (-) × (-) = + and (+) × (-) = -
How to Remember Order of Operations?
To remember the order of operations we use two famous acronyms, i.e. PEMDAS and BODMAS. We use either of the two according to the rules of order of operations. PEMDAS or BODMAS helps in remembering the process of solving any order of operation for any n number of expressions.
How to do Order of Operations with Exponents?
According to the PEMDAS, the letter E stands for exponents which come as the second step in order of operations. Let us look at the given example to clearly understand how to do the order of operations with exponents.
Expression: 7 × (22)
Solution: 7 × (4) = 28 (Correct (✔). This is a correct way to solve the exponents)
Let us look at another approach for the same expression.
7 × (22) = 142 = 196 ((Incorrect (✘). This is an incorrect way to do order of operations with exponents)
What is the Correct Order of Operations?
The correct order of operations can be easily expressed by using the word PEMDAS or BODMAS. The two words can be described as PEMDAS (Parentheses, Exponents, Multiplication or Division, and Addition or Subtraction). Similarly, for BODMAS (Brackets, Orders, Division, Multiplication, Addition, and Subtraction.)
What is the Order of Operations without Parentheses?
Going by the rules of the order of operations if we remove the parentheses, then we are left with EMDAS. EMDAS stands for (Exponents, Multiplication or Division, and Addition or Subtraction). If in the expression we don't have any exponential term then we need to perform multiplication or division first and moving forward we proceed with addition or subtraction. The situation may vary according to the operators present in the given expression
When Do We Use Order of Operations?
A lot of instances in our life pass through some sort of order of operations to perform it well. Every day we encounter such a scenario. For example, going to the grocery market and purchasing things we quickly perform the order of operations in our head. This helps us in reducing the turnaround time at the billing counter.
What Operation Is Completed First In the Order of Operations?
In the above sections, we read about two acronyms BODMAS and PEMDAS. According to both the acronyms, in order of operations, we simplify parentheses or the brackets first.
What is the Use of Order of Operation Calculator?
Order of operations calculator is an online tool and the fastest method with which we can evaluate any given numerical expression keeping the order of operations rules in mind. To use the order of operation calculator we need to enter the numerical expression in the correct format. Try Cuemath's order of operations calculator and solve the expressions quickly within a seconds.
☛Also Check:
For more practice try these:
- Order of Operations With Exponents Worksheets
- Advanced Order of Operations Worksheets
- Order of Operations Worksheets
What Are the 4 Order of Operations?
The 4 major order of operations are:
- Parentheses.
- An exponential term.
- Multiplication or division.
- At the end addition or subtraction.
The four order of operations can be easily recalled at any given point in time by learning the acronyms PEMDAS or BODMAS.