Sum of Infinite GP
The sum of infinite GP is the sum of an infinite number of terms of a geometric progression (GP). We may think that the sum of an infinite number of terms is infinity always. But this is NOT true in the case of an infinite GP. The sum of infinite GP is a finite number when the absolute value of its common ratio is less than 1.
Let us see what is the formula for the sum of infinite GP along with its proof.
| 1. | What is the Sum of Infinite GP? |
| 2. | Sum of Infinite GP When |r| < 1 |
| 3. | Sum of Infinite GP When |r| ≥ 1 |
| 4. | Sum of Infinite GP Formulas |
| 5. | FAQs on Sum of Infinite GP |
What is the Sum of Infinite GP?
The sum of infinite GP is nothing but the sum of infinite terms of a GP (Geometric Progression). A GP can be finite or infinite. In the case of an infinite GP, the formula to find the sum of its first 'n' terms is, Sn = a(1 - rn) / (1 - r), where 'a' is the first term and 'r' is the common ratio of the GP. But what if we have to find the sum of all terms of an infinite GP?
Consider the following sum: S = 1 + 1/2 + 1/4 + 1/8 +... of infinite terms. Will the sum be finite or infinite? This is a GP with the common ratio of magnitude less than 1. Note that all such GPs have finite sums. Let us find out the sum in this particular case. We take the original series for S, multiply it by the common ratio, and write the sums below each other.
S = 1 + 1/2 + 1/4 + 1/8 +... ___ (1)
Now, multiply each term on both sides by (1/2) (which is the common ratio):
S/2 = 1/2 + 1/4 + 1/8 +... ___ (2)
Then, we subtract the series (2) from series (1):
S - (S/2) = 1
S/2 = 1
S = 2
Thus, the sum of infinite terms of above GP is 2.
Wait! Can you think how come the sum of infinite GP is a finite number here? This is because, since the common ratio < 1, the terms become smaller and smaller. Let us find the sum of the first few terms here:
- S3 = 1 + 1/2 + 1/4 = 1.75
- S4 = 1 + 1/2 + 1/4 + 1/8 = 1.875
- S5 = 1 + 1/2 + 1/4 + 1/8 + 1/16 = 1.9375
- S6 = 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 = 1.96875
- S7 = 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 = 1.984375
- S8 = 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 = 1.9921875
- S9 = 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256 = 1.99609375
- S9 = 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + 1/512 = 1.998046875
Observe the last few sums. They all are very close to 2. Try calculating a few more sums. You don't get a sum that is more than 2. This is because going forward, we get the terms like 1/1024, 1/2048, 1/4096, ... which are very very small numbers (when simplified as decimals). If we continue calculating the terms as decimals, we get very very small numbers that are approximately equal to zero. In this way, the sum of infinite terms of GP gets converted into the sum of finite terms and hence the sum is a finite number.
Sum of Infinite GP When |r| < 1
We have already seen how to find the sum of infinite terms of GP. Let us derive a formula for the same. Consider a GP whose first term is 'a' and the common ratio is 'r' where |r| < 1. Then the sum of its infinite terms is:
S = a + ar + ar2 + ar3 + ...___ (1)
Multiply both sides by 'r':
rS = ar + ar2 + ar3 + ...___ (2)
Subtracting (2) from (1):
S - rS = a
S (1 - r) = a
Dividing both sides by (1 - r),
S = a / (1 - r)
This is the formula for infinite GP when r is less than 1.
Sum of Infinite GP When |r| ≥ 1
As we have seen in the example (in the first section), the sum of infinite GP is a finite number because, after a finite number of terms, the terms of GP are approximately equal to zero when |r| < 1. But when |r| ≥ 1, the GP would be something like 2, 4, 6, 8, 16, 32, 64, 128, 256, 512, 1024, .... where the numbers keep increasing and become very larger numbers after some point of time. Hence, the sum of a GP where |r| is greater than 1 cannot be found and in this case, the series diverges.
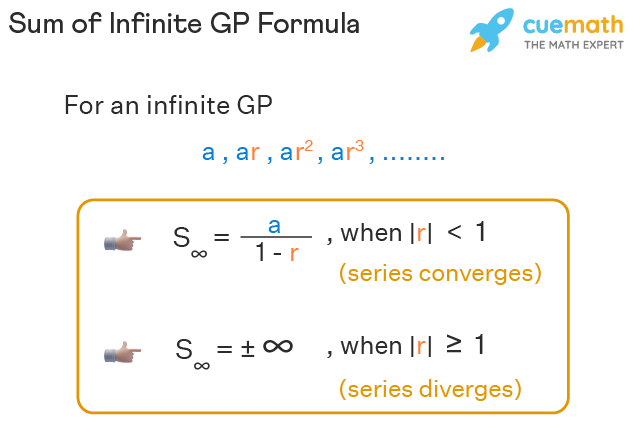
Sum of Infinite GP Formulas
By the previous two sections, we can summarize the sum of GP formulas as follows:
- S∞ = a / (1 - r) when |r| < 1
- S∞ = ±∞, when |r| ≥ 1
where 'a' is the first term and 'r' is the common ratio.
Examples:
- 1 + 1/2 + 1/4 + .... = 1 / (1 - 1/2) = 1 / (1/2) = 2
- 1 + 2 + 4 + ... = ∞
Important Notes on Sum of Infinite Terms of GP:
- The sum of infinite GP when |r| < 1 is, a / (1 - r).
- The sum of infinite GP when |r| ≥ 1 is ±∞.
☛ Related Topics:
Sum of Infinite GP Examples
-
Example 1: Find the following sums: (a) S = 1/3 + 1/9 + 1/27 + ... to ∞ (b) S = 1 - 1/2 + 1/4 - 1/8 + ... to ∞
Solution:
(a) Here, a = 1/3 and r = 1/3.
Here |r| = |1/3| = 1/3 < 1.
The sum of infinite GP is,
S = a / (1 - r)
= (1/3) / (1 - (1/3))
= (1/3) / (2/3)
= 1/2(b) Here, a = 1 and r = -1/2.
Here |r| = |-1/2| = 1/2 < 1.
The sum of infinite terms of GP is,
S = a / (1 - r)
= (1) / (1 - (-1/2))
= (2) / (3/2)
= 2/3Answer: (a) 1/2 (b) 2/3
-
Example 2: Is it possible to find the sum of the infinite geometric progression 3 - 6 + 12 - 24 + ....? Explain.
Solution:
In the given GP, r = -2.
Here, |r| = |-2| = 2 > 1.
Hence, the given series diverges and hence we can't find the sum of infinite GP.
Answer: Diverges.
-
Example 3: Find the sum: S = 1/3 + 1/52 + 1/33 + 1/54 + 1/35 + 1/56 + ... to ∞.
Solution:
The given sum can be split as the sum of the following two GPs:
S1 = 1/3 + 1/33 + 1/35 ... to ∞.
S2 = 1/52 + 1/54 + 1/56 + ... to ∞.
Using the formula for sum of infinite terms of GP:
For S1, a = 1/3 and r = 1/9. Hence, S1 = a/(1-r) = (1/3) / (1-1/9) = (1/3) / (8/9) = 3/8.
For S2, a = 1/25 and r = 1/25. Hence, S1 = a/(1-r) = (1/25) / (1-1/25) = (1/25) / (24/25) = 1/24.
Thus,
S = S1 + S2 = 3/8 + 1/24 = 10/24 = 5/12
Answer: 5/12.

FAQs on Sum of Infinite GP
What is the Sum of Infinite Terms in GP?
The sum of infinite terms in GP where 'a' is the first term and 'r' is the common ration is, a / (1 - r) when |r| < 1. But if |r| ≥ 1, then the sum diverges and hence we cannot apply the above formula.
How to Find the Sum of Infinite GP when r < 1?
When r < 1 (in particular when |r| < 1), the sum of infinite GP is, S∞ = a / (1 - r), where
- a = first term of GP
- r = common ratio of GP
How to Find the Sum of Infinite GP when r > 1?
When either |r| > 1 or |r| = 1, the terms of the GP are very large going forward and hence the sum diverges. We cannot find the sum of infinite GP in such cases.
Can we Find Infinite GP Sum Always?
No, we can find the infinite GP sum only when the absolute value of the common ratio is strictly less than 1. i.e., |r| < 1. In this case, the sum = a/(1-r), where 'a' represents the first term of GP.
What is the Difference Between the Sum of an Infinite GP and a Finite GP?
For a GP a, ar, ar2, ar3, ...
- Sum of finite (n) terms is, Sn = (1-rn)/(1-r).
- Sum of infinite terms is, S∞ = a/(1-r) (when |r| < 1).
visual curriculum