How To Find Interquartile Range
In this mini-lesson, we shall explore the topic of interquartile range, by finding answers to questions like what is meant by interquartile range, how to find interquartile range, and what is the formula for interquartile range.
Before we look into the theory of the interquartile range, let us check through this simulation to understand the interquartile range.
Simulation - Interquartile Range Calculator
Follow these two quick steps, to calculate the interquartile range.
Step 1: Fill the box for the number of data points, and click on 'new data set'.This would be the required data.
Step 2: Click on 'show data' , and further click on \(Q_1 \), \(Q_3 \), \(Q_3 - Q_1 \) buttons to see the respective values.
Now with this understanding from the above simulation, let's move ahead to know more about the interquartile range.
Lesson Plan
What is Meant by Interquartile Range?
The interquartile range is the distance between the first quartile and the third quartile.
\[ \text{ Interquartile range} = Q_3 - Q_1 \]
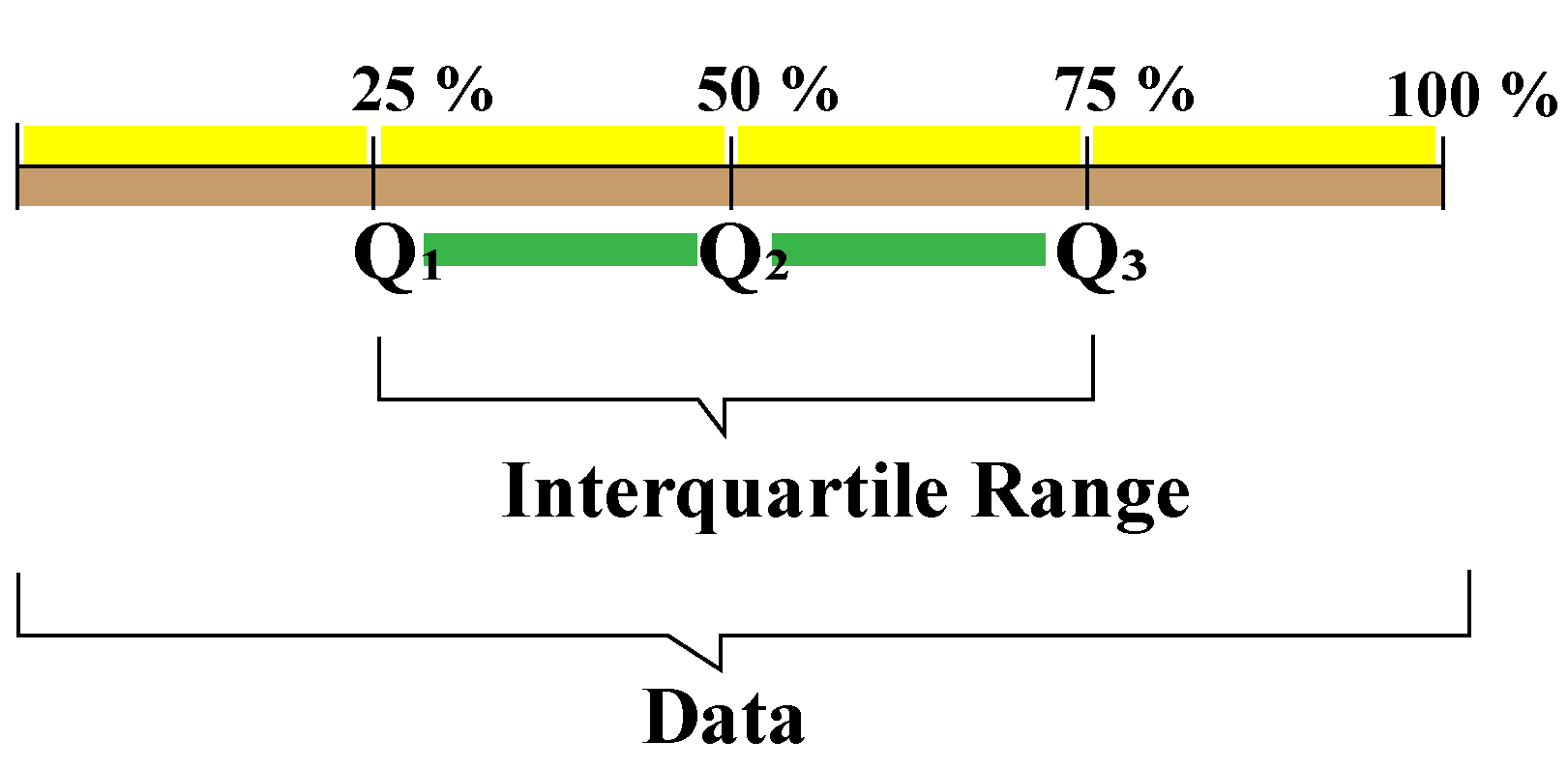
First Quartile - \(Q_1 \): It is the data point located midway between the median and the smallest number of the given data. It divided the data at the 25% mark
Third Quartile -\(Q_3 \): It is the data point located midway between the median and the highest number of the given data. It divides the data at the 75% mark.
How to Find an Interquartile Range?
There are three simple steps to find the interquartile range.
STEP - 1: Arrange the data in ascending or descending order.
STEP - 2: Find the first quartile and the third quartile value.
STEP - 3: The difference between the first and the third quartile value is the interquartile range.

- James picks up the given set of random two-digit numbers.
43, 36, 49, 22, 29, 55, 63, 12, 17, 30, 51, 77, 96
Can you help James to find the interquartile range for the above set of numbers?
What is the Interquartile Formula?
The formulae for the interquartile range is as follows:
Interquatile range (IQR) = \(Q_3 - Q_1 \)

The interquartile range is useful to find the outlier fences. The data beyond the outlier fences are the outliers. Euler's method is used to define the outlier fence. The upper outlier fence is \(Q_3 + 1.5\,IQR \) and the lower outlier fence is \(Q_1 + 1.5\,IQR \).
Can you calculate the outlier fence for the data - 44, 11, 23, 19, 74, 8, 33, 50, 29, 21, 17, 16, 12, 41, 93 and identify the outliers?
Solved Examples
| Example 1 |
George finds the first quartile and the third quartile values of the data to be 43 and 71 respectively. How can you further help George to find the interquartile range for this data?
Solution
The known values are:
\(Q_1 = 43 \) and \(Q_3 = 71 \)
Interquartile range = \(Q_3 - Q_1 = 71 - 43 = 28 \)
|
\(\therefore \) The interquartile range is 28 |
| Example 2 |
Peter wants to know the interquartile range of the set of the first 100 whole numbers. How can you help Peter?
Solution
Listing the first 100 natural numbers, we have 1, 2, 3, ..........98, 99, 100
Taking the first half of the data, 1, 2, 3,.......48, 49, 50 we can find the first quartile value.
First Quartile = \(Q_1 = \dfrac{25 + 26}{2} = \dfrac{51}{2} = 25.5 \)
Now taking the second half of the data, 51, 52,53, ....... 98, 99,100 we can find the third quartile value.
Third Quartile = \(Q_3 = \dfrac{75 + 76}{2} = \dfrac{151}{2} = 75.5 \)
Interquartile range = \(Q_3 - Q_1 = 75.5 - 25.5 = 50 \)
|
\(\therefore \) The interquartile range is 50 |
| Example 3 |
What is the interquartile range of the data which includes the first 20 multiples of the number 12?
Solution
The multiples of 12 are 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144, 156, 168, 180, 192, 204, 216, 228, 240 <<add and before 240: ...216, 228, and 240>>
The first half of the data is 12, 24, 36, 48, 60, 72, 84, 96, 108, and 120
First Quartile = \(Q_1 = \dfrac{60 + 72}{2} = \dfrac{132}{2} = 66 \)
And the second half of the data is 132, 144, 156, 168, 180, 192, 204, 216, 228, and 240
Third Quartile = \(Q_3 = \dfrac{180 + 192}{2} = \dfrac{372}{2} = 186 \)
Interquartile range = \(Q_3 - Q_1 = 186 - 66 = 120 \)
|
\(\therefore \) The interquartile range is 120 |
Interactive Questions on Interquartile Range
Here are a few activities for you to practice. Select/Type your answer and click the "Check Answer" button to see the result.
Let's Summarize
The mini-lesson targeted the fascinating concept of the interquartile range. The math journey around the interquartile range starts with what a student already knows, and goes on to creatively crafting a fresh concept in the young minds. Done in a way that not only it is relatable and easy to grasp, but also will stay with them forever. Here lies the magic with Cuemath.
About Cuemath
At Cuemath, our team of math experts is dedicated to making learning fun for our favorite readers, the students!
Through an interactive and engaging learning-teaching-learning approach, the teachers explore all angles of a topic.
Be it worksheets, online classes, doubt sessions, or any other form of relation, it’s the logical thinking and smart learning approach that we, at Cuemath, believe in.
FAQs on Interquartile Range
1. How do you find the interquartile range?
The interquartile range is the difference between the first and the third quartile of the data. The maximum part of the data lies within the interquartile range.
2. What is IQR rule?
The IQR rule is as follows.
\[ \text{Interquartile Range(IQR) = Third Quartile - First Quartile}\]
3. What is the interquartile range of the dataset?
The interquartile range of the dataset is the difference between the first and third quartile of the dataset.
4. How to make a box and whisker plot?
To draw a box plot, arrange the data in ascending order, and identify the first quartile and the third quartile. Draw the box plot with the first quartile and the third quartile as the boundaries. The lines which extend beyond the box is called the whiskers and it represents the remaining data outside the first and third quartile. The outliers are marked as points on the whiskers.
5. What is the lower quartile?
For the given data, arrange it into ascending order and divide it into four equal parts. The datapoint which divides the data into 25% and 75% is called the lower quartile.
Also, the lower quartile is a data point that divides the first half of the data into two equal parts.
6. What is the upper quartile?
Arrange the data in ascending order and divide it into four equal parts. The datapoint above the median, which divides it into 75% and 25% is called the upper quartile.
Further, the upper quartile is a data point, which divides the second half of the data into two equal parts.
7. How do you find quartile and interquartile ranges?
The first quartile is the data point which marks the first 25% of the data. The third quartile is the data point which marks 75% of the data.
The interquartile range is the difference between the first and the third quartile of the data. \[ \text{Interquartile Range(IQR) = Third Quartile - First Quartile}\]
8. What do we use the interquartile range for?
We use an interquartile range to avoid outliers. Also, the maximum part of the data exists within the interquartile range.
- Live one on one classroom and doubt clearing
- Practice worksheets in and after class for conceptual clarity
- Personalized curriculum to keep up with school