Special Right Triangles
Special right triangles are those right-angled triangles whose interior angles are fixed and whose sides are always in a defined ratio. There are two types of special right triangles, one which has angles that measure 45°, 45°, 90°; and the other which has angles that measure 30°, 60°, 90°. Let us learn about the special right triangle formulas along with a few solved examples.
| 1. | What are Special Right Triangles? |
| 2. | Special Right Triangle Formula |
| 3. | FAQS on Special Right Triangles |
What are Special Right Triangles?
Special right triangles are the triangles in which all the 3 interior angles are defined and the sides have a fixed ratio. In these right-angled triangles, we can find the value of 2 missing sides if one side is given. The two special right triangles are also known as the 45°- 45°- 90° triangle and the 30°- 60°- 90° triangle. Before reading about it in detail, let us recollect the few basic properties of a right triangle:-
- In a right triangle, one of the angles is 90°, and the sum of the other two angles adds up to 90°
- The side opposite to the right angle is called the hypotenuse and is the longest side of the triangle.
45° 45° 90° triangle
A 45° 45° 90° triangle is an isosceles right triangle, as we can see that 2 of its acute angles are equal to 45°. The ratio of its legs and hypotenuse is expressed as follows: Leg : Leg : Hypotenuse = 1: 1: √2. In terms of x, it can be expressed as x: x: x√2, as shown in the figure given below.

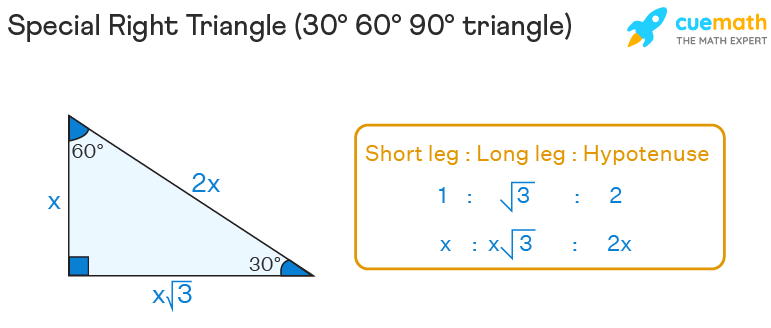
30° 60° 90° triangle
A 30 - 60 - 90 triangle is one in which the acute angles are 30° and 60° respectively. The ratio of its legs and hypotenuse is expressed as follows: Short leg : Long leg : Hypotenuse = 1: √3: 2. In terms of x, it can be expressed as x: x√3: 2x, as shown in the figure given below.
Special Right Triangle Formula
The right triangle formula is the basic Pythagoras theorem formula which says that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. However, in the case of special right triangles, we use the particular ratios which act as formulas and they help to calculate the missing sides of a triangle even when one side is known. The special right triangle formulas in the form of ratios can be expressed as:
- 30° 60° 90° triangle formula: Short leg: Long leg : Hypotenuse = x: x√3: 2x
- 45° 45° 90° triangle formula: Leg : Leg: Hypotenuse = x: x: x√2
Let us use these formulas in some examples and see how we can find the 2 missing sides when only one side is given.
Example: The longer side of a 30° 60° 90° triangle is 4√3 units. Find the length of its hypotenuse and the other side.
Solution:
- We know that the ratio of a 30° 60° 90° triangle is expressed as, Short leg: Long leg : Hypotenuse = x: x√3: 2x. This means 2x is the hypotenuse and x is the shorter side and x√3 is the longer side.
- So, the longer side can be written as, x√3 = 4√3, which means the value of x = 4 units.
- So, the dimensions of the missing sides can be calculated after substituting the value of x = 4.
- This means, the shorter side is 4 units, the longer side is 4√3 units and the hypotenuse is 2 × 4 = 8 units.
- Therefore, the length of the hypotenuse is 8 units, and the other leg is 4 units.
Let us use the special right triangle formula with another example taking a 45° 45° 90° triangle.
Example: If the hypotenuse of a 45° 45° 90° triangle is 3√2 units, what is the length of its other two legs.
Solution:
- We know that the ratio of a 45° 45° 90° triangle is given as, Leg : Leg: Hypotenuse = x: x: x√2.
- It is given that the hypotenuse is equal to 3√2, so we can say that x√2 = 3√2. This gives the value of x = 3.
- Now the dimensions of the missing sides can be calculated after substituting the value of x = 3.
- This means the other two equal legs are 3 units each while the hypotenuse is 3√2 units.
- Therefore, the other two legs are 3 units each.
☛ Related Topics
Examples Using Special Right Triangle Formula
-
Example 1: Find the long leg and the hypotenuse of a 30° 60° 90° triangle if its short leg is equal to 5√3 units.
Solution: Short leg = 5√3; Long leg = ?, hypotenuse = ?
The special right triangles formula of a 30° 60° 90° triangle is: Short leg: Long leg : Hypotenuse = x: x√3: 2x
We will substitute the values in x : x√3: 2x; where x = short leg, x√3 = long leg, 2x = hypotenuse
This means, short leg = 5√3 = x
So, the length of the long leg = (5√3)√3= 5 × 3 = 15 units
And, hypotenuse = 2x = 2 × 5√3 = 10√3 units
Answer: The long leg of the triangle = 15 units, and the hypotenuse of the triangle = 10√3 units.
-
Example 2: If one leg of a 45° 45° 90° triangle is 5 units, find the length of the other leg and the hypotenuse.
Solution: One leg = 5 units, Second leg = ?, Hypotenuse = ?
The special right triangles formula of a 45° 45° 90° triangle is: Leg : Leg: Hypotenuse = x: x: x√2
We will substitute the values in x: x: x√2; where x = the equal legs, x√2 = hypotenuse.
One leg = 5 = x
So, the length of the other leg = 5 units (because this is an isosceles right triangle in which the two legs are of equal length.
And hypotenuse = √2x =√2 × 5 = 5√2 units
Answer: The second leg of the triangle = 5 units, and the hypotenuse of the triangle = 5√2 units.
-
Example 3: Can a right triangle have 11 in, 60 in, and 61 in as its dimensions?
Solution:
If 11, 60, and 61 are Pythagorean triples, then they will form a right triangle.
So, let us substitute these values in the Pythagoras theorem formula and check. According to the Pythagoras theorem, a2 + b2 = c2, where a and b are the two sides and c is the hypotenuse. Since the longest side of a right-angled triangle is the hypotenuse we substitute the values as:
a2 + b2 = c2
112 + 602 = 612
121 + 3600 = 3721
3721 = 3721
Hence, the given numbers form a Pythagorean triple and can be the dimensions of a right triangle.Answer: 11 in, 60 in, and 61 in can be the possible dimensions of a right triangle.

FAQs on Special Right Triangles
What are the 2 Special Right Triangles?
The 2 special right triangles are those right-angled triangles in which all the interior angles are defined and whose sides have a fixed ratio.
- The 45°, 45°, 90° triangle - This triangle has angles that measure 45°, 45°, 90°, and the ratio of their sides is given as: Leg : Leg : Hypotenuse = 1: 1: √2
- The 30°, 60°, 90° triangle - This triangle has angles that measure 30°, 60°, 90°, and the ratio of their sides is given as: Short leg : Long leg : Hypotenuse = 1: √3: 2
What is the Special Right Triangle Formula in Geometry?
The formula for the 2 types of special right triangles is expressed in the form of the ratio of the sides and can be written as follows:
- 30° 60° 90° triangle formula: Short leg: Long leg : Hypotenuse = x: x√3: 2x
- 45° 45° 90° triangle formula: Leg : Leg: Hypotenuse = x: x: x√2
What are the Applications of the Special Right Triangle Formula?
There are numerous applications of the right triangle in real life, the most common is its use in the branch of trigonometry as the relation between its angles and sides form the basis for trigonometry. It is further utilized in the construction and engineering field.
How to Solve a Special Right Triangle?
Solving a special right triangle means finding the missing sides when one of the sides is given. The two special right triangles have a specific ratio of its sides. This is useful to find the missing sides. Let us observe these ratios that are given below.
- 30° 60° 90° triangle formula: Short leg: Long leg : Hypotenuse = x: x√3: 2x
- 45° 45° 90° triangle formula: Leg : Leg: Hypotenuse = x: x: x√2
How to find the Hypotenuse of a Special Right Triangle 30-60-90?
In order to find the hypotenuse of a special right triangle 30-60-90, we can use the formula or ratio that is defined for its sides. We know that in this kind of triangle, Short leg: Long leg : Hypotenuse = x: x√3: 2x. Therefore, if we know the sides we can easily substitute the values and calculate the length of the hypotenuse. For example, if the short leg of a 30-60-90 triangle is given as 6 units, then we can substitute the value in the given ratio, which will be, x: x√3: 2x = 6 : 6√3 : 12. This shows that the hypotenuse is 12 units.
How to find the Hypotenuse of a Special Right Triangle 45-45-90?
In order to find the hypotenuse of a special right triangle 45-45-90, we can use the formula or ratio that is defined for its sides. We know that in this kind of triangle, Leg : Leg: Hypotenuse = x: x: x√2. Therefore, if we know the sides we can substitute the given values and calculate the length of the hypotenuse. For example, if the length of the leg of a 30-60-90 triangle is given as 4 units, then we can substitute the value in the given ratio, which will be, x: x: x√2 = 4 : 4: 4√2. This shows that the hypotenuse is 4√2 units.
visual curriculum