A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
LearnPracticeDownload

Area of Right Triangle

The area of a right triangle is the region that is covered inside the boundary of the right triangle. A right-angled triangle is a triangle in which one of the angles is a right angle (90 degrees). Let us learn more about the area of a right-angled triangle, how to find the area of a right-angled triangle with hypotenuse, along with some examples.

1. What is Area of a Right Triangle?
2. Area of Right Triangle Formula
3. Derivation of Area of Right Angled Triangle Formula
4. Area of Right Triangle with Hypotenuse
5. FAQs on Area of a Right Triangle

What is Area of a Right Triangle?

The area of a right-angled triangle is the space that is inside it. Before learning about the area of a right angled triangle, let us see a right-angled triangle.

In a right-angled triangle, the side opposite to the right angle is called the hypotenuse and the other two sides are called legs. The two legs can be interchangeably called base and height. Observe the following figure which shows a right angled triangle along with its formula.

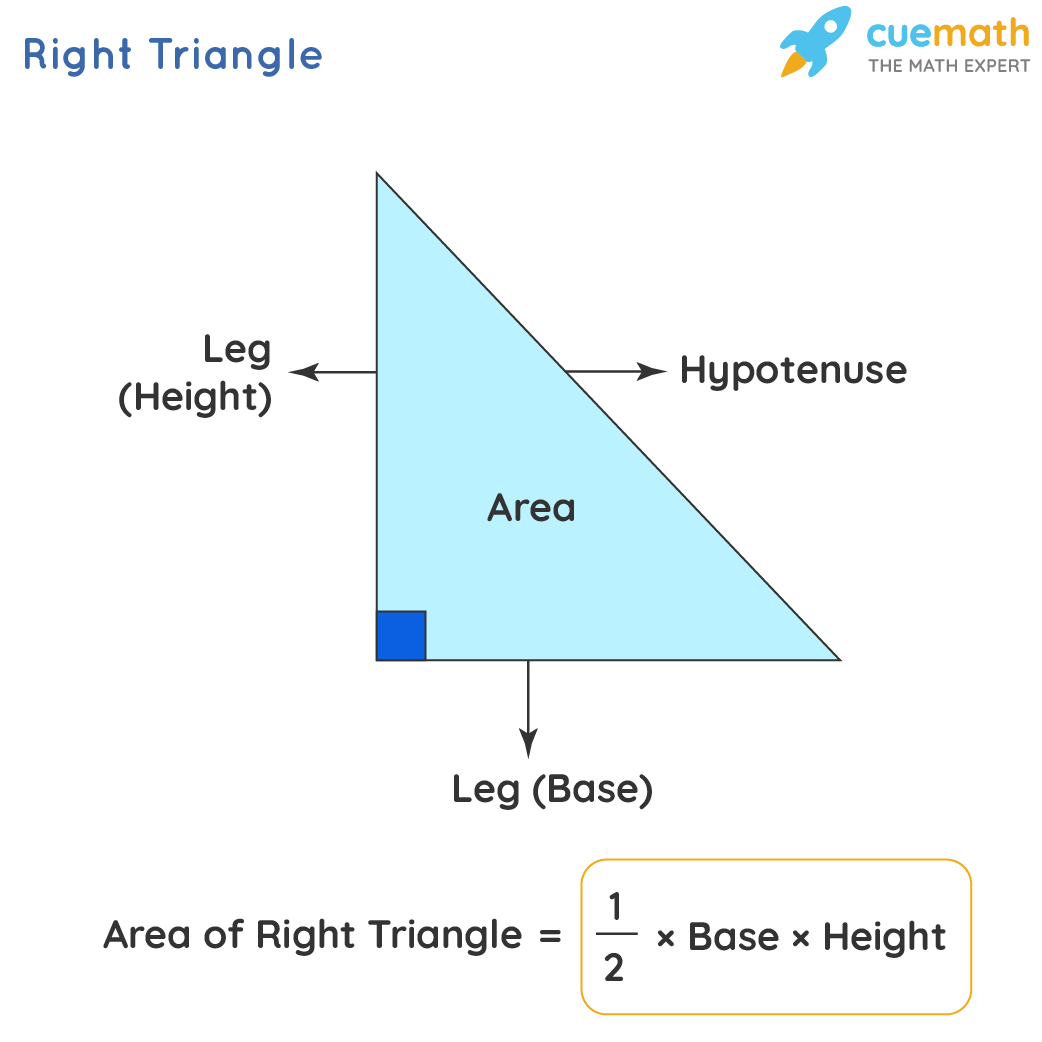
area of right triangle - area of a right angled triangle = 1/2 x base x height

Area of Right Triangle Formula

The formula for the area of a right-angled triangle is expressed as:

Area of a right triangle = 1/2 × base × height

So, let us use this formula in the following examples.

Example: Find the area of a right triangle with base 4 cm and height 6 cm.

Solution: It is given that base = 4 cm, height = 6 cm

So, let us find the area of the triangle using the formula,

Area of right angled triangle = 1/2 × base × height

After substituting the values in the formula, we get,

Area of right angled triangle = 1/2 × 4 × 6 = 12 square cm

Therefore, the area of a right triangle with base 4 cm and height 6 cm is 12 cm2

Example: Find the area of a right triangle with a base of 3 cm and a height of 1.42 cm.

Solution: It is given that base = 3 cm, height = 1.42 cm

So, let us find the area of the triangle using the formula,

Area of right angled triangle = 1/2 × base × height

After substituting the values in the formula, we get,

Area of right angled triangle = 1/2 × 3 × 1.42 = 2.13 square cm.

Therefore, the area of a right triangle with a base of 3 cm and a height of 1.42 cm is 2.13 cm2

Derivation of Area of Right Angled Triangle Formula

The formula for the area of a right angled triangle can be derived easily using the following steps.

How to prove the formula of area of a right triangle?

  • Step 1: Consider a rectangle of length l and width w and draw a diagonal as shown above. We can see that the diagonal divides the rectangle into two right triangles.
  • Step 2: It is to be noted that these two right triangles are congruent. We also know that the formula for the area of a rectangle = length × width.
  • Step 3: So, the area of one right triangle will be half the area of a rectangle. This can be expressed as, Area of one right triangle = 1/2 × length × width. Since we usually represent the legs of the right-angled triangle as base and height, the formula for the area of a right triangle can be expressed as, Area of a right triangle = 1/2 × base × height.

Area of Right Triangle With Hypotenuse

The area of a right triangle can be calculated using the hypotenuse as well. Let us recollect the Pythagoras theorem which states that in a right-angled triangle, the square of the hypotenuse is the sum of the squares of the other two sides, i.e., (Hypotenuse)2 = (Base)2 + (Height)2

We can find the area of a right angled triangle if we know the length of one of the legs along with the hypotenuse. Let us understand this with the help of an example.

Example: Find the area of a right triangle with base 6 cm and hypotenuse 10 cm.

Solution: It is given that base = 6 cm, hypotenuse = 10 cm. So, we can find the value of the missing leg (height) using the Pythagoras theorem.

Let us substitute the given values in the Pythagoras theorem,

(Hypotenuse)2 = (Base)2 + (Height)2

102 = 62 + (Height)2

100 = 36 + (Height)2

(Height)2 = 64

Height = √(64) = 8 cm

Now, we can find the area of the given right triangle in which base = 6 cm, height = 8 cm

After substituting the values in the formula, we get,

Area of right angled triangle = 1/2 × base × height = 1/2 × 6 × 8 = 24 cm2.

 

Area of Right Triangle Examples

  1. Example 1: The longest side of a right triangle is 13 units. If its height is 12 units, find its area using the area of a right triangle formula.

    Solution:

    We know that the longest side of a right triangle is called the hypotenuse.

    So, it is given that hypotenuse = 13 units and height = 12 units. We can find the length of the base using the Pythagoras theorem.

    After substituting the given values in the Pythagoras theorem,

    (hypotenuse)2 = (base)2 + (height)2

    132 = (base)2 + (12)2

    169 = (base)2 + 144

    (base)2 = 25

    base = √(25) = 5 units.

    Now, we can calculate the area of the right-angled triangle with base = 5 units, height = 12 units

    The area of the right triangle = 1/2 × base × height = 1/2 × 5 × 12 = 30 square units.

    Therefore, the area of the right triangle = 30 square units.

  2. Example 2: A swimming pool is in the shape of a right triangle. Its sides are in the ratio 3:4:5. Its perimeter is 720 units. Find its area.

    Solution:

    Let us assume that the sides of the swimming pool be 3x, 4x, and 5x.

    It is given that its perimeter = 720 units.

    3x + 4x + 5x = 720

    12x = 720

    x = 60

    So the sides of the triangle are,

    3x = 3(60) = 180 units

    4x = 4(60) = 240 units

    5x = 5(60) = 300 units

    Since 300 units is the longest side of the swimming pool (which is in the shape of a right triangle), it is the hypotenuse.

    So, 180 units and 240 units must be the base and the height of the swimming pool interchangeably.

    Using the area of right angled triangle formula,

    The area of the swimming pool = 1/2 × base × height = 1/2 × 180 × 240 = 21,600 units2.

    Therefore, the area of the given swimming pool = 21,600 units2.

  3. Example 3: Find the area of a right triangle whose base is 1.2 m and hypotenuse is 3.7 m.

    Solution:

    It is given that base = 1.2 m, hypotenuse = 3.7 m. So, we can find the value of the missing leg (height) using the Pythagoras theorem.

    Let us substitute the given values in the Pythagoras theorem,

    (Hypotenuse)2 = (Base)2 + (Height)2

    (3.7)2 = (1.2)2 + (Height)2

    13.69 = 1.44 + (Height)2

    (Height)2 = 12.25

    Height = √(12.25) = 3.5 m

    Now, we can find the area of the given right triangle in which base = 1.2 m, height = 3.5 m

    After substituting the values in the formula, we get,

    Area of right angled triangle = 1/2 × base × height = 1/2 × 1.2 × 3.5 = 2.1 m2.

Show Solution >

go to slidego to slidego to slide

Breakdown tough concepts through simple visuals.
Math will no longer be a tough subject, especially when you understand the concepts through visualizations.

Book a Free Trial Class

FAQs on Area of Right Triangle

What is the Area of a Right Triangle?

The area of a right triangle is defined as the total space or region covered by the right-angled triangle. It is expressed in square units. Some common units used to represent area are m2, cm2, in2, yd2, etc.

What is the Formula of Area of a Right Triangle?

The formula which is used to find the area of a right triangle is expressed as, Area of right triangle = 1/2 × base × height. Here base and height are the two legs of the right-angled triangle while the third side is the hypotenuse.

How to Find the Perimeter and Area of a Right Triangle?

The area of a right triangle is found using the formula, Area of right triangle = 1/2 × base × height, where base and height are the two legs of the right-angled triangle. Observe the figure of a right-angled triangle given above on this page to identify the legs. The perimeter of a right triangle is obtained by adding all the 3 sides of the triangle. In case only two of its sides are given, then we use the Pythagoras theorem to find the third side.

How to Find the Area of a Right Triangle Without the Base?

If only the height and hypotenuse of a right triangle are given, then before finding the area of the triangle, we first need to find the base using the Pythagoras theorem. After calculating the base, we can use the following formula to find its area, Area of right triangle = 1/2 × base × height. For example, to find the area of a right triangle with a height of 4 cm and hypotenuse 5 cm, we first need to find its base using the Pythagoras theorem. This means, base = √[(hypotenuse)2 - (height)2] = √(52 - 42) = √9 = 3 cm. After this, we can find the area as follows. Area of the right triangle = 1/2 × base × height = 1/2 × 3 × 4 = 6 cm2.

How to Find the Area of a Right Angled Triangle Without the Height?

If only the base and hypotenuse of a right-angled triangle are given, then before finding the area of the triangle, we first need to find the height using the Pythagoras theorem. Then we can use the formula, Area of right angled triangle = 1/2 × base × height, to find its area. For example, to find the area of a right triangle with a base of 4 cm and hypotenuse 5 cm, we first find its height using the Pythagoras theorem. So, we get, height = √[(hypotenuse)2 - (base)2] = √(52 - 42) = √9 = 3 cm. After this step, we can find the area as follows. Area of the right triangle = 1/2 × base × height = 1/2 × 3 × 4 = 6 cm2.

How to Find the Area of Right Angled Triangle With Hypotenuse?

The area of a right-angled triangle can be calculated if we know the value of the hypotenuse and one of its legs.

  • If we know the base of the right triangle and the hypotenuse, we can find the height using the Pythagoras theorem.
  • If we know the height of the right triangle and the hypotenuse, we can find the base using the Pythagoras theorem.
  • Then, we can find the area of the right triangle using the formula 1/2 × base × height.
Download FREE Study Materials
Area of Right Triangle Worksheet
Math worksheets and
visual curriculum