Right Triangle Formulas
A triangle is a closed figure or shape with 3 sides, 3 angles, and 3 vertices, and for right triangle formulas, the properties have to be more specific. If any one of the angles of a triangle is a right angle (measuring 90º), the triangle is called a right-angled triangle or simply, a right triangle. Right triangle formulas would help you solve various calculations related to the perimeter, area, etc of the right triangle.
What Are the Right Triangle Formulas?
A right-angled triangle is one which has one of its interior angle measuring 90 degrees. Right-angled triangle formulas are used to calculate the perimeter, area, height, etc of a right triangle using its three sides.
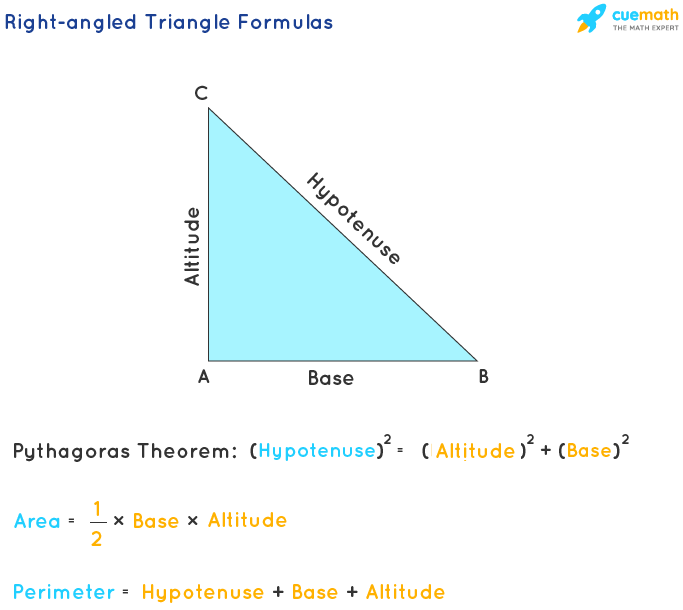
Right-angled Triangle Formula
Different formulas associated with the right triangle are:
- Pythagoras Theorem - Formula
The Pythagoras theorem definition shows the relation among the three sides of a right triangle. The square of the hypotenuse is equal to the sum of the square of the other two sides.
(Hypotenuse)2 = (Perpendicular)2 + (Base)2
- Area of a right triangle formula
The formula to calculate the area of a right triangle formula is given as:
Area = 1/2 × Base × Height = 1/2 × b × h
where height,h is equal to the length of the perpendicular side of the triangle.
- The perimeter of a right triangle formula
The formula to calculate the area of a right triangle formula is given as:
Perimeter = a + b + c
where a, b, and c are the three sides of the triangle.

Examples Using Right Triangle Formulas
Example 1: The length of the base and perpendicular of a right-angled triangle is 6 in and 8 in respectively. Find:
- Length of its hypotenuse
- The perimeter of the triangle
- Area of the triangle
Solution:
To find:
Given: length of base = 6 in, length of perpendicular = 8 in
i) Using Pythogoras' theorem,
(Hypotenuse)2 = (Base)2 + (Perpendicular)2
(Hypotenuse)2 = 62 + 82 = 100
Hypotenuse = √100 = 10 in
ii) Using the perimeter of a right triangle formula,
Perimeter = Sum of all sides
Perimeter = 6 + 8 + 10 = 24 in
iii) Using the area of triangle formula,
Area = (1/2) × b × h
= (1/2) × 6 × 8
= 24 in2
Answer: Hypotenuse of the right triangle = 10 in, the perimeter of the right triangle = 24 in, and the area of the right triangle = 24 in2.
Example 2: The height and hypotenuse of a right-angled triangle measure 12 in and 13 in respectively. Find its area.
Solution:
To find: Area of a right-angled triangle
Given: Height = 12 in, Hypotenuse = 13 in
Using Pythagoras' theorem,
(13)2 = (Base)2 + (12)2
(Base)2 = (13)2 - (12)2 = 25
Base = √25 = 5 in
Using the Area of a triangle formula,
Area = (1/2) × b × h
Area = (1/2) × 5 × 12
Area = 30 in2
Answer: Area of the right-angled triangle = 30 in2
Example 3: Determine the area of a right-angled triangle whose perimeter is 30 units, height is 12 units, and the hypotenuse is 13 units
Solution:
To find: Area of a right-angled triangle
Given: perimeter = 30 units, hypotenuse = 13 units, height = 12 units
We know that perimeter = base + hypotenuse + height
30 units = 13 + 12 + base
Therefore, base = 30 - 25 = 5 units
Area = 1/2bh = 1/2(5×12) = 30 sq units.
Answer: Area of the right-angled triangle = 30 unit2
FAQs on Right Triangle Formulas
What Is Right Triangle Formula in Geometry?
In geometry, the right triangle formulas are formulas of the right triangle that are used to calculate the perimeter, area, height, etc of the triangle using three of its sides - base, height, and hypotenuse. These formulas are given as:
- Pythagoras Theorem - Formula: (Hypotenuse)2 = (Perpendicular)2 + (Base)2
- Area of a right triangle formula: Area = 1/2 × Base × Height
- Perimeter of a right triangle formula = Sum of lengths of 3 sides
What Are the Applications of Right Triangle Formula?
There are numerous applications of the right triangle in real life, the most common is its use in the branch of trigonometry as the relation between its angles and sides form the basis for trigonometry. It is further utilized in the construction and engineering field.
How To Calculate Area of Right Triangle Using Right Triangle Formula When its Perimeter, Height, and Base are Given?
In order, to calculate the area of the right triangle when its perimeter, height, and base are given, we will consider only two parameters - height and base.
- Step 1: Check for the given values.
- Step 2: Put the values of height h and base b in the area formula, (1/2)bh
How to Find the Height of a Right Triangle Formula?
The height of a right triangle can be calculated, given the length of base and height of a right triangle formula can be calculated using the Pythagoras theorem as, (Hypotenuse)2 = (Height)2 + (Base)2. Substitute the known values and solve for the height or perpendicular of the right triangle.
visual curriculum