30-60-90 Triangle
A 30-60-90 triangle is a special right-angled triangle as the angles of the triangle are in the ratio 1:2:3. There are different types of triangles such as obtuse, isosceles, acute, equilateral, and so on. But only a few types of triangles are considered special triangles. These triangles are special as their sides and angles are consistent and predictable. Their properties can be used to solve various geometry or trigonometry problems. A 30-60-90 triangle—pronounced "thirty sixty ninety"—is one such very special type of triangle indeed.
In this lesson, we will explore the concept of the 30-60-90 triangle and learn all about it including its formula, definition, sides, area, and the rules that apply to this triangle.
| 1. | What is 0-60-90 Triangle? |
| 2. | 30-60-90 Triangle Sides |
| 3. | 30-60-90-Triangle Theorem |
| 4. | 30-60-90 Triangle Proof |
| 5. | 30-60-90 Triangle Rule |
| 6. | Area of a 30-60-90 Triangle |
| 7. | FAQS on 30-60-90 Triangle |
What is 30-60-90 Triangle?
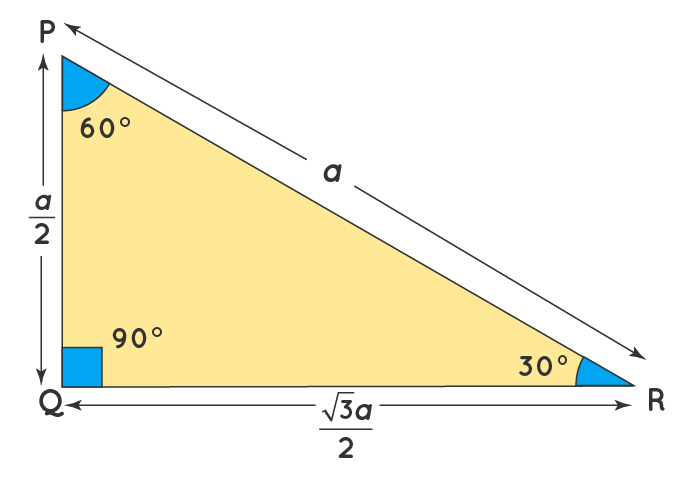
The 30-60-90 triangle is called a special right triangle as the angles of this triangle are in a unique ratio of 1:2:3. Here, a right triangle means being any triangle that contains a 90° angle. A 30-60-90 triangle is a special right triangle that always has angles of measure 30°, 60°, and 90°. Here are some of the variants of a 30-60-90 triangle. The triangles ABC and PQK are 30-60-90 triangles.

Here, in the triangle ABC, ∠ C = 30°,∠ A = 60°, and ∠ B = 90° and in the triangle PQK, ∠ P = 30°,∠ K = 60°, and ∠ Q = 90°
30-60-90 Triangle Sides
A 30-60-90 triangle is a special triangle since the length of its sides is always in a consistent relationship with one another.
In the below-given 30-60-90 triangle ABC, ∠ C = 30°,∠ A = 60°, and ∠ B = 90°. We can understand the relationship between each of the sides from the below definitions:
- The side that is opposite to the 30° angle, AB = y will always be the smallest since 30° is the smallest angle in this triangle
- The side that is opposite to the 60° angle, BC = y × √3 = y√3 will be the medium length because 60° is the mid-sized degree angle in this triangle
- On the side that is opposite to the 90° angle, the hypotenuse AC = 2y will be the largest side because 90° is the largest angle.
The sides of a 30-60-90 triangle are always in the ratio of 1:√3: 2. This is also known as the 30-60-90 triangle formula for sides y: y√3: 2y. Let us learn the derivation of this ratio in the 30-60-90 triangle proof section. This formula can be verified using the Pythagoras theorem.

Consider some of the examples of a 30-60-90 degree triangle with these side lengths:
|
|
|
|
Here, in the 30-60-90 triangle DEF ∠ F = 30°,∠ D = 60°, and ∠ E = 90°
|
Here, in the 30-60-90 triangle PQR ∠ R = 30°,∠ P = 60°, and ∠ Q = 90°
|
30-60-90-Triangle Theorem
The statement of the 30-60-90-Triangle Theorem is given as,
Statement: The length of the hypotenuse is twice the length of the shortest side and the length of the other side is √3 times the length of the shortest side in a 30-60-90-Triangle.
30-60-90-Triangle Formula
The above theorem can be written mathematically as the 30-60-90-Triangle Formula as 1:√3: 2 which is the ratio of the three sides of the 30-60-90-Triangle. Another formula for this special triangle 1:2:3 which is the ratio of the three angles of the 30-60-90-Triangle.
30-60-90-Triangle Proof
Let's consider an equilateral triangle ABC with a side length equal to 'a'.
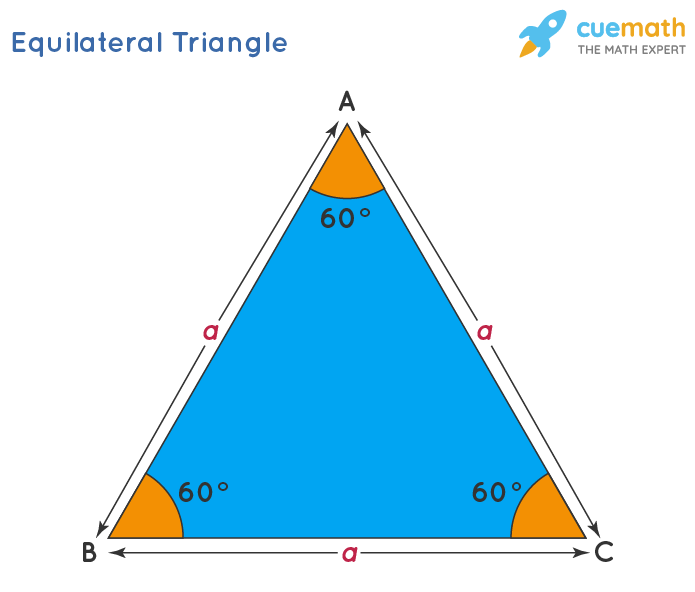
Now, draw a perpendicular from vertex A to side BC at point D of the triangle ABC. The perpendicular in an equilateral triangle bisects the other side.

Triangle ABD and ADC are two 30-60-90 triangles. Both the triangles are similar and right-angled triangles. Hence, we can apply the Pythagoras theorem to find the length AD.
(AB)2 = (AD)2 + (BD)2
a2 = (AD)2 + (a/2)2
a2 - (a/2)2 = (AD)2
3a2/4 = (AD)2
(a√3)/2 = AD
AD = (a√3)/2
BD = a/2
AB = a
These sides also follow the same ratio a/2 : (a√3)/2: a
Multiply by 2 and divide by 'a',
(2a)/(2a) : (2a√3)/(2a): (2a/a)
We get 1:√3:2. This is the 30-60-90 triangle theorem.
30-60-90 Triangle Rule
In a 30-60-90 triangle, the measure of any of the three sides can be found out by knowing the measure of at least one side in the triangle. This is called the 30-60-90 triangle rule. The below-given table shows how to find the sides of a 30-60-90 triangle using the 30-60-90 triangle rule:
| Base is given | Perpendicular is given | Hypotenuse is given |
|---|---|---|
|
|
|
|
|
The Base BC of the triangle is assumed to be 'a'. |
The perpendicular DE of the triangle is assumed to be 'a'. |
The hypotenuse PR of the triangle is assumed to be 'a'. |
|
The perpendicular of the triangle ABC is AB = (a /√3) The hypotenuse of the triangle ABC is AC = (2a)/√3 |
The base of the triangle DEF is EF = √3a. The hypotenuse of the triangle DEF is DF = 2a. |
The base of the triangle PQR is QR = (√3a)/2. The perpendicular of the triangle PQR is PQ = (a/2). |
Area of a 30-60-90 Triangle
The formula to calculate the area of a triangle is = (1/2) × base × height. In a right-angled triangle, the height is the perpendicular of the triangle. Thus, the formula to calculate the area of a right-angle triangle is = (1/2) × base × perpendicular
Let's learn how to apply this formula to find the area of the 30-60-90 triangle.

Base BC of the triangle is assumed to be 'a', and the hypotenuse of the triangle ABC is AC. We have learned in the previous section how to find the hypotenuse when the base is given.
Let's apply the formula we have learned.
Thus, perpendicular of the triangle = a/√3
Area of the triangle = (1/2) × base × perpendicular
Area = 1/2 × a × a/√3
Therefore, the area of the 30-60-90 triangle when the base (side of middle length) is given as 'a' is: a2/(2√3)
Related Articles
Important Notes on 30-60-90 Triangle
Here is a list of a few points that should be remembered while studying 30-60-90 triangles:
- The 30-60-90 triangle is called a special right triangle as the angles of this triangle are in a unique ratio of 1:2:3 and the sides are in the ratio 1:√3: 2
- A 30-60-90 triangle is a special right triangle that always has angles of measure 30°, 60°, and 90°
- All the sides of a 30-60-90 triangle can be calculated if any one side is given. This is called the 30-60-90 triangle rule.
Solved Examples on 30-60-90 Triangle
-
Example 1: Find the length of the hypotenuse of a right-angle triangle if the other two sides are 8 and 8√ 3 units.
Solution:
First, let's check the ratio to verify if it is suitable for a 30-60-90 triangle.
The ratio of the two sides = 8:8√3 = 1:√3
This indicates that the triangle is a 30-60-90 triangle. We know that the hypotenuse is 2 times the smallest side.
Thus, the hypotenuse is 2 × 8 = 16 units
Answer: Hypotenuse = 16 units
-
Example 2: A triangle has sides 2√2, 2√6, and 2√8. Find the angles of this triangle.
Solution:
The sides of the triangle are 2√2, 2√6, and 2√8.
First, let's check whether the sides are following the 30-60-90 triangle rule.
2√2: 2√6: 2√8 can be re-written as 2√2: 2√2 × √3: 2 × 2√2
If we divide the ratio by 2√2, we get 1:√3: 2
These sides are following the 30-60-90 triangle rule. We know that the angles of a 30-60-90 triangle are 30°,60°, and 90°.
Answer: The angles of the triangle are 30°,60°, and 90°.
-
Example 3: Verify if the triangle is a 30-60-90 triangle if the sides of the triangle are 4 units, √48 units, and 8 units.
Solution: To verify if the triangle is a 30-60-90 triangle, we will check the ratio of the sides. We have
4 : √48 units : 8 = 4 : 4√3 : 4 × 2
= 1 : √3 : 2
Using the 30-60-90 triangle theorem, the sides are in the ratio 1 : √3 : 2. So the triangle is a 30-60-90 triangle.
Answer: The given triangle is a 30-60-90 triangle.

FAQs on 30-60-90 Triangle
What Is a 30-60-90 Triangle?
The 30-60-90 triangle is called a special right triangle as the angles of this triangle are in a unique ratio of 1:2:3. A 30-60-90 triangle is a special right triangle that always has angles of measure 30°, 60°, and 90°.
What Is the Perimeter of a 30-60-90 Triangle?
The perimeter of a 30 60 90 triangle with the smallest side equal to a is the sum of all three sides. The other two sides are a√3 and 2a. The perimeter of the triangle is a+a√3+2a = 3a+a√3 = a√3(1+√3).
Are There Any Tips for Remembering the 30-60-90 Triangle Rules?
This method can be used to remember the 30-60-90 triangle rule. One can remember it as 1, 3, 2; it can resemble the ratio of the sides, all one needs to remember is that the middle term is √3
What Are the Side Lengths of a 30-60-90 Triangle?
The sides of a 30-60-90 triangle have a set pattern. The side that is opposite to the 30° angle, 'y' will always be the smallest since 30° is the smallest angle in this triangle. The side that is opposite to the 60° angle, y√3 will be the medium length because 60° is the mid-sized degree angle in this triangle. The side that is opposite to the 90° angle, 2y will be the largest side because 90° is the largest angle.
What Are the Rules for a 45-45-90 Triangle?
A 45-45-90 triangle has a right angle and two 45 degree angles. The two sides of a 45-45-90 triangle are always equal and the hypotenuse of the triangle is always opposite to the right angle.
What Are Some Similarities Between 30-60-90 Triangles and 45-45-90 Triangles?
These are some of the similarities between 30-60-90 triangle and 45-45-90 triangle: both are not acute triangles, both are right-angle triangles, both are not obtuse triangles, the square of the hypotenuse equals the sum of the squares of the other two sides for both triangles, and the sum of the interior angles of both are 180°.
Which Leg is the Long Leg in the 30-60-90 Triangle?
The long leg of a 30-60-90 Triangle is the leg whose length is greater than the shortest leg and ess than the hypotenuse. The length of the long leg is equal to √3 times the length of the shortest leg.
visual curriculum