Solutions of Linear Equation
Solutions of Linear Equation refer to the set of values of the variables in the linear equations giving all possible solutions. Linear equations involve unknown quantities in the form of one or more variables to represent real-life problems. It helps in finding out the cost, mileage, speed, and distance, etc. with ease. We all use linear equations in our daily life without knowing.
In this lesson, let us learn in detail about the solutions of linear equations, types of solutions, and how to find the solutions, etc.
What are the Solutions of a Linear Equation?
The solutions of linear equations are the points at which the lines or planes representing the linear equations intersect or meet each other. A solution set of a system of linear equations is the set of values to the variables of all possible solutions. For example, while solving linear equations one can visualize the solution of a system of simultaneous linear equations by drawing 2 linear graphs and finding out their intersection point.

The red line represents all the solutions for equation 1, and the blue line, solutions for equation 2. The intersection at a unique point (2,4) is the solution that will satisfy both equations.
Types of Solutions for Linear Equations
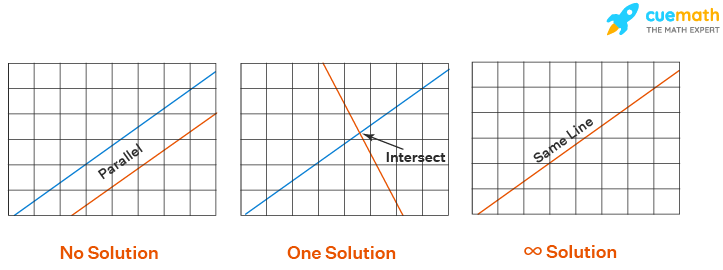
A system of linear equations can have 3 types of solutions.
Unique Solution of a system of linear equations
The unique solution of a linear equation means that there exists only one point, on substituting which, L.H.S and R.H.S of an equation become equal. The linear equation in one variable has always a unique solution. For example, 3m =6 has a unique solution m = 2 for which L.H.S = R.H.S. Similarly, for simultaneous linear equations in two variables, the unique solution is an ordered pair (x,y) which will satisfy both the equations.
No Solution
A system of linear equations has no solution when there exists no point where lines intersect each other or the graphs of linear equations are parallel.
Infinite Many Solutions
A system of linear equations has infinitely many solutions when there exists a solution set of infinite points for which L.H.S and R.H.S of an equation become equal, or in the graph straight lines overlap each other.
How to find the Solution of a Linear Equation?
Solutions for Linear Equations in One Variable
Consider the equation, 2x + 4 = 8
- To find the value of x, first, we remove 4 from L.H.S, so we subtract 4 from both sides of the equation. 2x + 4 - 4 = 8 - 4
- Simply. Now we get, 2x = 4
- Now we have to remove 2 from L.H.S in order to get x, therefore we divide the equation by 2. 2x/2 = 4/2, x=2
Hence, the solution of the equation 2x + 4 = 8 is x=2.
Solutions for Linear Equations in Two Variables
The following methods can be used to find the solutions of linear equations of two variables.
Substitution Method
Consider the following pair of linear equations, let's solve the following linear equations.
x + y = 4 and x - y = 2
- Let’s rearrange the first equation to express y in terms of x, as follows: x + y = 4, y = 4 - x
- This expression for y can now be substituted in the second equation, so that we will be left with an equation in x alone: x - y = 2, x - 4 + x = 2, 2x = 6 x = 6/2, x = 3
- Once we have the value of x, we can plug this back into any of the two equations to find out y. Lets plug it into the first equation: x + y = 4 (3) + y = 4, y = 4 - 3 = 1, y = 1
- The final non trivial solution is: x = 3, y = 1
It should be clear why this process is called substitution. We express one variable in terms of another using one of the pair of equations and substitute that expression into the second equation.
Elimination Method
Consider the following pair of linear equations:
2x + 3y - 11 = 0, 3x + 2y - 9 = 0
The coefficients of x in the two equations are 2 and 3 respectively. Let us multiply the first equation by 3 and the second equation by 2, so that the coefficients of x in the two equations become equal:
- 3 {2x + 3y - 11 = 0} 6x + 9y - 33 = 0
- 2 {3x + 2y - 9 = 0} 6x + 4y - 18 = 0
Now, let us subtract the two equations, which means that we subtract the left-hand sides of the two equations, and the right-hand side of the two equations and the equality will still be preserved.
6x + 9y - 33 = 0 ,6x + 4y - 18 = 0 0 + 5y - 15 = 0, 5y = 15, y = 3
Note how x gets eliminated, and we are left with an equation in y alone. Once we have the value of y, we proceed as earlier – we plug this into any of the two equations. Let us put this into the first equation:
2x + 3y - 11 = 0, 2x + 3 (3) - 11 = 0, 2x + 9 - 11 = 0\, 2x = 2, x = 1
Thus, the non trivial solution is: x = 1, y = 3
Graphical Method
As an example, lets solve the following linear equation: x - y + 2 = 0, 2x + y - 5 = 0. We draw the corresponding lines on the same axes:

The point of intersection is (1,3), which means that x = 1, y = 3 is a solution to the pair of linear equations given by (2). In fact, it is the only solution to the pair, as two non-parallel lines cannot intersect at more than one point.
Important Notes
You can check directly about the types of solutions using the following conditions:
- Unique solution (consistent and independent) a1/a2 ≠ b1/b2
- No solution (inconsistent and independent) a1/a2 = b1/b2 ≠ c1/c2
- Infinite many solutions (consistent and dependent) a1/a2 = b1/b2 = c1/c2
Examples of Solutions of Linear Equation
-
Example 1: Tom loves to collect ¢2 and ¢5 coins in his piggy bank. He knows that the total sum in his piggy bank is ¢77, and it has 3 times as many two-cent coins as five-cent coins in it. He wants to know the exact number of ¢2 and ¢5 coins in his piggy bank. Can you help him find the count?
Solution:
Let the number of ¢5 coins be x.
The number of ¢2 coins will be 3x.
Total amount = 5x + 2(3x)
Thus, 5x + 2(3x) = 77
5x + 6x = 77
11x = 77
x = 7Therefore, Tom has 7 coins ¢5 of and 21 coins of ¢2.
-
Example 2: In a river, a boat can travel 40 miles upstream in 2 hours. The same boat can travel 60 miles downstream in 2 hours.
- What is the speed of the boat in still water?
- What is the speed of the current?
Solution:
Let us assume that:
- the speed of boat in still water = x miles per hour
- the speed of current = y miles per hour.
During upstream, the current pulls back the boat's speed and the speed of the boat during upstream = \(x-y\).
During downstream, the current's speed adds to the boat's speed and the speed of the boat during downstream = \(x+y\).
Thus,
Distance(d) Time(t) Speed Speed=d/t UPSTREAM 40 miles 2 hr x - y 40/2=20 DOWNSTREAM 60 miles 2 hr x + y 60/2=30 Using the last two columns of the table:
x - y = 20 -------(1)
x + y = 30 -------(1)
Adding (1) and (2):
2x = 50, x =25
Substitute this in (2):
y = 30-25, y =5
The speed of boat = 25 miles per hour
The speed of current = 5 miles per hour

FAQs on Solutions of Linear Equations
How To Solve the System of Linear Equations?
We have different methods to solve the system of linear equations:
- Graphical method
- Substitution method
- Cross-multiplication method
- Elimination method
- Determinants method
What Is a Unique Solution for a Linear Equation?
The unique solution of a system of linear equations is an ordered pair or point which makes equality true in the equation.
What Happens If a Pair of Linear Equations Is Consistent?
If a pair of linear equations is consistent then the lines either intersect or coincide with (overlap) each other.
What Are the 3 Solutions To Linear Equations?
There are three ways to solve systems of linear equations: substitution, elimination, and graphing
How Do You Find the Solution of a Linear System?
- First, solve one linear equation for y in terms of x.
- Then substitute that expression for y in the other linear equation. You'll get an equation in x .
The lines intersect at zero points.
The lines intersect at exactly one point.
The lines intersect at infinitely many points.
How Do You Find the Solution of Two Linear Equations?
Solving Systems of Equations by Substitution
- Solve one of the two equations for one of the variables in terms of the other.
- Substitute the expression for this variable into the second equation, then solve for the remaining variable.
How Do You Solve Linear Equations One Variable?
- Step 1: Simplify each side, if needed.
- Step 2: Use Add./Sub. Properties to move the variable term to one side and all other terms to the other side.
- Step 3: Use Mult./Div. ...
- Step 4: Check your answer.
How Many Solutions of the Linear Equation 2x-5y=7 Are There?
In the given equation 2x – 5y = 7, for every value of x, we get a corresponding value of y and vice-versa. Therefore, the linear equation has infinitely many solutions.
How To Find Ordered Pair Solutions of Linear Equations?
To figure out if an ordered pair is a solution to an equation, you could perform a test. Identify the x-value in the ordered pair and plug it into the equation. When you simplify, if the y-value you get is the same as the y-value in the ordered pair, then that ordered pair is indeed a solution to the equation.
How Do You Find the Ordered Pair Solution of a Linear Equation in Two Variables?
To check that an ordered pair is a solution, substitute the corresponding x- and y-values into each equation and then simplify to see if you obtain a true statement for both equations.
visual curriculum