Factorization of Algebraic Expressions

Factorization of algebraic expressions means finding the factors of the given expression which refers to finding two or more expressions whose product is the given expression. This process of finding two or more expressions whose product is the given expression is known as the factorization of algebraic expressions. A factor is a number that divides the given number without any remainder. It simply means expressing a number as a multiplication of two other numbers. Similarly, in Algebra we write the algebraic expressions as a product of their factors. The only difference here is that an algebraic expression involves numbers and variables combined with an arithmetic operation like addition or subtraction.

In this lesson, we will learn about factorization, how to factorize algebraic expressions using various methods, and identities with solved examples practice questions.

'Factor' is a term used to express a number as a product of any two numbers. Factorization is a method of finding factors for any mathematical object, be it a number, a polynomial or any algebraic expression. Thus, factorization of an algebraic expression refers to finding out the factors of the given algebraic expression.

For example, the factors of 10 are 1,2,5, and 10. Similarly, an algebraic expression can also be factorized. When the factors are multiplied they result in the original number or an expression that is factorized. For example, consider the expression (2x²+8x). It can be factorized as 2x(x+4). When we multiply (2x) and (x+4), we get the original expression (2x²+8x).

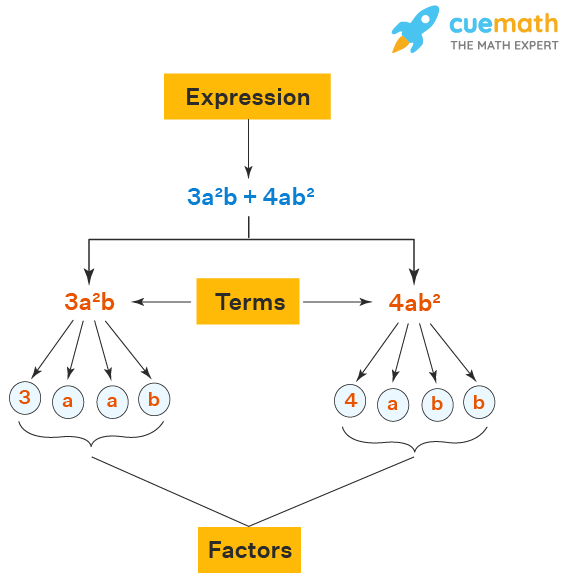
We know that an algebraic expression is made up of terms. For example, the term \(\begin{align} 7xy \end{align}\) can be factorized as \(\begin{align} 7 \times x \times y \end{align}\). This term cannot be factorized further.

Now let us explore the methods used to factorize algebraic expressions.

Factorization of Algebraic Expressions using Common Factor Method

Follow the steps given below to find the factors of the expression: \(\begin{align} x^2 + 4x\end{align}\)

• Step 1: \(\begin{align} x^2 \end{align}\) can be factorized as \(\begin{align} x \times x \end{align}\), and \(\begin{align} 4x\end{align}\) can be factorized as \(\begin{align}x \times 2 \times x \end{align}\).
• Step 2: Find the greatest common factor of the two terms. Here, we see that \(\begin{align} x\end{align}\) is the greatest common factor. We keep this factor outside the brackets, divide the polynomial terms by this factor and write the remaining expression inside the brackets.
• Step 3: Thus, the expression is factorized as \(\begin{align} x(x + 4)\end{align}\)

Factorization of Algebraic Expressions by Regrouping Terms

In some algebraic expressions, all the terms may not have a particular factor in common. Consider the algebraic expression 15x + y - xy - 15.

• Step 1: Look for the terms with common factors. Only the first and last term has a common factor of 15. Similarly, the second and third term has a common factor y.
• Step 2: Thus, the terms can be regrouped as 15x + y - xy - 15 = 15x - 15 + y - xy
• Step 3: Take out common factors.15x - 15 - xy - y = 15(x -1) - y(x -1). Clearly, (a-1) is a common factor.
• Step 4: Thus, the factorization of the given expression 15x - 15 - xy - y = (x -1) (15 -y)

Thus, by regrouping the terms in a given algebraic expression, we can factorize that algebraic expression.

Factorization of Algebraic Expressions Using Identities

This method involves formulas of algebraic expression for factorization.

• Example 1: \(\begin{align} x^2 + 6x + 9\end{align}\)

We see that there are no common factors for the three terms in the expression. However, in the expression, we see that \(\begin{align} 9\end{align}\) is a perfect square.In this case, we seek the help of algebraic identities to factorize the expression easily. This expression looks similar to the identity: \(\begin{align}(a+b)^2 = a^2 + 2ab +b^2\end{align}\). Comparing the given expression to the identity, we get \(\begin{align}a = x, b = 3\end{align}\)

Therefore, the factors are \(\begin{align}(x+3)^2\end{align}\) or \(\begin{align}(x+3) (x+3)\end{align}\)

• Example 2: \(\begin{align}16x^2 - 25y^2\end{align}\)

In this expression, we see that there are no common factors. Also, we see that this expression is of the form: \(\begin{align}a^2 - b^2 = (a+b)(a-b)\end{align}\). Comparing the given expression to the identity, we get \(\begin{align}a = 4x, b = 5y\end{align}\).

Therefore, the factors are \(\begin{align}(4x + 5y) (4x - 5y)\end{align}\)

Listed below are the formulas of algebraic expressions.

• \(\begin{align}(a+b)^2 = a^2 + 2ab +b^2\end{align}\)
• \(\begin{align}(a-b)^2 = a^2 - 2ab +b^2\end{align}\)
• \(\begin{align}a^2 - b^2 = (a+b)(a-b)\end{align}\)
• \(\begin{align}a^3 + b^3 = (a+b)(a^2-ab+b^2)\end{align}\)
• \(\begin{align}a^3 - b^3 = (a-b)(a^2+ab+b^2)\end{align}\)
• \(\begin{align}(a+b)^3 = a^3 + 3a^2b+3ab^2+b^3\end{align}\)
• \(\begin{align}(a-b)^3 = a^3 - 3a^2b+3ab^2-b^3\end{align}\)

Important Notes

• Factoring an algebraic expression means writing the expression as a product of factors.
• To verify whether the factors are correct or not, multiply them and check if you get the original algebraic expression.
• Algebraic expressions can be factorized using the common factor method, regrouping like terms together, and also by using algebraic identities.
• To find the factors of a monomial is the same as finding the factors for a whole number. For example, \(\begin{align}27x^2\end{align}\) can be factorized as \(\begin{align}9 \times 3 \times x \times x\end{align}\)
• While factoring algebraic expressions, check if they are in the form of any identity. In this case, you can find the factors using the formula of the identity.

What is Factorization of Algebraic Expressions in Math?

An algebraic expression that is expressed as a product of factors that consists of variables, constants, and arithmetic operators is called factorization of algebraic expressions.

How To Factorize Algebraic Expressions?

Algebraic Expressions can be factorized using many methods. The most common methods used for factorization of algebraic expressions are:

• Factorization using common factors.
• Factorization by regrouping terms.
• Factorization using identities.

What Are the Methods of Factorization of Algebraic Expressions?

Factorization can be done by finding common factors, grouping like terms, and using identities.

How Do You Factorize Algebraic Expressions Using the Common Factor Method?

To factorize using the common factor method, we find the highest common factor and place it before the brackets. Then, divide the polynomial terms by this highest common factor to obtain the expression inside the brackets.

How To Do Factorization of Algebraic Expressions Using Identities?

There are three standard identities for factorization of algebraic expressions.

• \(\begin{align}(a+b)^2 = a^2 + 2ab +b^2\end{align}\)
• \(\begin{align}(a-b)^2 = a^2 - 2ab +b^2\end{align}\)
• \(\begin{align}a^2 - b^2 = (a+b)(a-b)\end{align}\)