(a - b)^3 Formula
The (a - b)^3 formula is used to find the cube of a binomial which is made up of the difference of two terms. It says (a - b)3 = a3 - 3a2b + 3ab2 - b3. This is one of the algebraic identities.
This formula is used to calculate the cube of the difference between two terms very easily and quickly without doing complicated calculations. Let us learn more about a minus b whole cube formula along with solved examples.
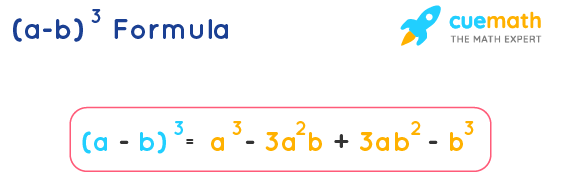
What is the (a - b)^3 Formula?
The (a-b)^3 formula is used to calculate the cube of a binomial. The formula is also known as the cube of the difference between two terms. According to "a minus b whole cube formula",
(a - b)3 = a3 - 3a2b + 3ab2 - b3 (or) a3 - b3 - 3ab (a - b)
We can derive this formula in two ways:
- Method 1: By expanding (a - b)3 as (a - b) (a - b) (a - b).
- Method 2: By using the formula of (a + b)3
Derivation of (a - b)^3: Method 1
To find the formula of (a - b)3, we will just multiply (a - b) (a - b) (a - b).
(a - b)3 = (a - b)(a - b)(a - b)
= (a2 - 2ab + b2)(a - b)
= a3 - a2b - 2a2b + 2ab2 + ab2 - b3
= a3 - 3a2b + 3ab2 - b3 (or)
= a3 - b3 - 3ab (a - b)
Therefore, (a - b)3 formula is:
(a - b)3 = a3 - 3a2b + 3ab2 - b3
Hence proved.
Derivation of (a - b)^3: Method 2
We use the formula of (a + b)3 to derive the formula of a minus b whole cube. We know that
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Replace b with -b on both sides of this formula:
(a + (-b))3 = a3 + 3a2(-b) + 3a(-b)2 + (-b)3
This results in (a - b)3 = a3 - 3a2b + 3ab2 - b3.
Hence derived.

Examples on (a - b)^3 Formula
Example 1: Solve the following expression using (a - b)3 formula:
(2x - 3y)3
Solution:
To find: (2x - 3y)3
Using (a - b)3 Formula,
(a - b)3 = a3 - 3a2b + 3ab2 - b3
= (2x)3 - 3 × (2x)2 × 3y + 3 × (2x) × (3y)2 - (3y)3
= 8x3 - 36x2y + 54xy2 - 27y3
Answer: (2x - 3y)3 = 8x3 - 36x2y + 54xy2 - 27y3
Example 2: Find the value of x3 - y3 if x - y = 5 and xy = 2 using (a - b)3 formula.
Solution:
To find: x3 - y3
Given:
x - y = 5
xy = 2
Using (a - b)3 Formula,
(a - b)3 = a3 - 3a2b + 3ab2 - b3
Here, a = x; b = y
Therefore,
(x - y)3 = x3 - 3 × x2 × y + 3 × x × y2 - y3
(x - y)3 = x3 - 3x2y + 3xy2 - y3
53 = x3 - 3xy(x - y) - y3
125 = x3 - 3 × 2 × 5 - y3
x3 - y3 = 155
Answer: x3 - y3 = 155
Example 3: Solve the following expression using (a - b)3 formula: (5x - 2y)3
Solution:
To find: (5x - 2y)3
Using (a - b)3 Formula,
(a - b)3 = a3 - 3a2b + 3ab2 - b3
= (5x)3 - 3 × (5x)2 × 2y + 3 × (5x) × (2y)2 - (2y)3
= 125x3 - 150x2y + 60xy2 - 8y3
Answer: (5x - 2y)3 = 125x3 - 150x2y + 60xy2 - 8y3
FAQs on (a - b)^3 Formula
What is the Expansion of a Minus b Whole Cube Formula?
a minus b whole cube formula is denoted by (a - b)3. Its expansion is expressed as (a - b)3 = a3 - 3a2b + 3ab2 - b3.
What s the (a - b)3 Formula in Algebra?
The (a - b)3 formula is also known as one of the important algebraic identities. It is read as a minus b whole cube. Its (a - b)3 formula is expressed as (a - b)3 = a3 - 3a2b + 3ab2 - b3.
What is the Formula of a Minus b Minus c Whole Cube?
The formula for (a - b - c)3 is (a - b - c)3 = a3 - b3 - c3 + 3 (a - b) (- b - c) (-c + a).
How To Simplify Numbers Using the (a - b)3 Formula?
Let us understand the use of the (a - b)3 formula with the help of the following example.
Example: Find the value of (20 - 5)3 using the (a - b)3 formula.
To find: (20 - 5)3
Let us assume that a = 20 and b = 5.
We will substitute these in the formula of (a - b)3.
(a - b)3 = a3 - 3a2b + 3ab2 - b3
(20-5)3 = 203 - 3(20)2(5) + 3(20)(5)2 - 53
= 8000 - 6000 + 1500 - 125
= 3375
Answer: (20 - 5)3 = 3375.
How To Use the (a - b)3 Formula?
To use a minus b whole cube formula, first write the formula (a - b)3 = a3 - 3a2b + 3ab2 - b3. Then substitute the values of a and b here. Finally, simplify.
visual curriculum