Algebra Formulas

Algebra Formulas form the foundation of numerous topics of mathematics. Topics like equations, quadratic equations, polynomials, coordinate geometry, calculus, trigonometry, and probability, extensively depend on algebra formulas for understanding and for solving complex problems. The algebra formulas are helpful to perform complex calculations in the least time and with fewer steps. The algebraic expression formulas are used to simplify the algebraic expressions.

Based on the complexity of the math topics, the algebraic formulas have also been transformed. Topics like logarithms, indices, exponents, progressions, permutations, and combinations have their own set of algebraic formulas. Here, we shall look into the list of all algebraic formulas used across the different math topics.

1.	Algebra Formulas - Identities
2.	What are Algebra Formulas?
3.	Algebraic Formulas for Class 8
4.	Algebraic Formulas for Class 9
5.	Algebraic Formulas for Class 10
6.	Algebraic Formulas for Class 11
7.	Algebraic Formulas for Class 12
8.	Algebra Formulas of Functions
9.	Algebra Formulas of Fractions
10.	FAQs on Algebra Formulas

In algebra formulas, an identity is an equation that is always true regardless of the values assigned to the variables. Algebraic Identity means that the left-hand side of the equation is identical to the right-hand side of the equation, and for all values of the variables. Algebraic identities find applications in solving the values of unknown variables. Here are some most commonly used algebraic identities:

Algebraic Identities Formula

• (a + b)² = a² + 2ab + b²
• (a - b)² = a² - 2ab + b²
• (a + b)(a - b) = a² - b²
• (x + a)(x + b) = x² + x(a + b) + ab

Let us look at the algebraic identity: (a + b)² = a² + 2ab + b², and try to understand this identity in algebra and also in geometry. As proof of this formula, let us try to multiply algebraically the expression and try to find the formula. (a + b)² = (a + b) × (a + b) = a(a + b) + b(a + b) = a² + ab + ab + b². This expression can be geometrically understood as the area of the four sub-figures of the below-given square diagram. Further, we can consolidate the proof of the identity (a + b)²= a² + 2ab + b².

In the same way, by using squares and rectangles, we can prove the other algebraic identities as well.

An algebraic formula is an equation or a rule written using mathematical and algebraic symbols and terms. It is an equation that involves algebraic expressions on both sides. The algebraic formula is a short quick formula to solve complex algebraic calculations. These algebraic formulas can be derived for each maths topic, usually having an unknown variable x, and some of the common algebraic formulas can be applied to each of the maths topics.

Example: (a+b)² = a² + 2ab + b² is an algebraic formula and here,

• (a+b)² is an algebraic expression
• a² + 2ab + b² is a simplified form of an algebraic expression

Here are the algebraic formulas arranged class-wise.

• Algebraic Formulas for Class 8
• Algebraic Formulas for Class 9
• Algebraic Formulas for Class 10
• Algebraic Formulas for Class 11
• Algebraic Formulas for Class 12

Let us look at the detailed list of these formulas in the upcoming sections.

The algebra formulas for three variables a, b, and c and for a maximum degree of 3 can be easily derived by multiplying the expression by itself, based on the exponent value of the algebraic expression. The below formulas are for class 8.

• (a + b)² = a² + 2ab + b²
• (a - b)² = a² - 2ab + b²
• (a + b)(a - b) = a² - b²
• (a + b)³ = a³ + 3a²b + 3ab² + b³
• (a - b)³ = a³ - 3a²b + 3ab² - b³
• a³ + b³ = (a + b)(a² - ab + b²)
• a³ - b³ = (a - b)(a² + ab + b²)
• (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca

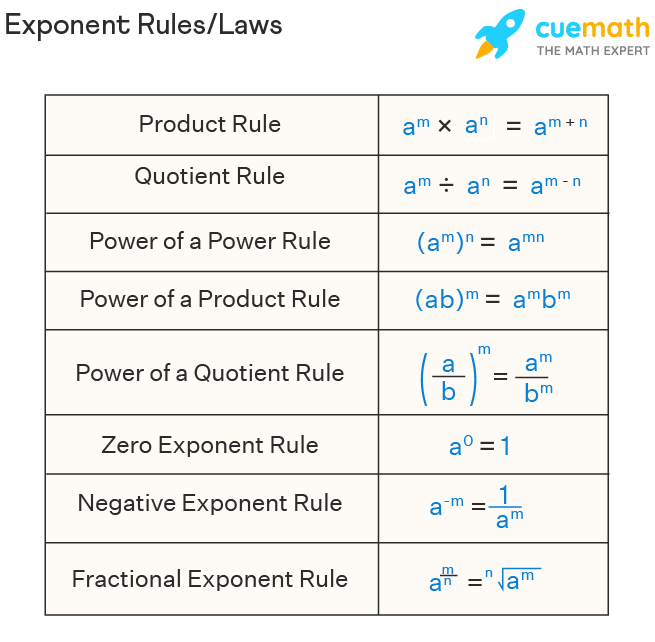
Some of the common laws of exponents with the same bases having different powers, and different bases having the same power, are useful to solve complex exponential terms. The higher exponential values can be easily solved without any expansion of the exponential terms. These exponential laws are further useful to derive some of the logarithmic laws.

• a^m. aⁿ = a^{m + n}
• a^m/aⁿ = a^{m - n}
• (a^m)ⁿ = a^mn
• (ab)^m = a^m. b^m
• a⁰ = 1
• a^-m = 1/a^m

Each of these laws has a specific name. Take a look at the figure below:

Logarithms are useful for the computation of highly complex multiplication and division calculations. The normal exponential form of 2⁵ = 32 can be transformed to a logarithmic form as log₂ 32 = 5. Further, the multiplication and division between two mathematic expressions can be easily transformed into addition and subtraction, after converting them to logarithmic form. The below properties of logarithms formulas are applicable in logarithmic calculations.

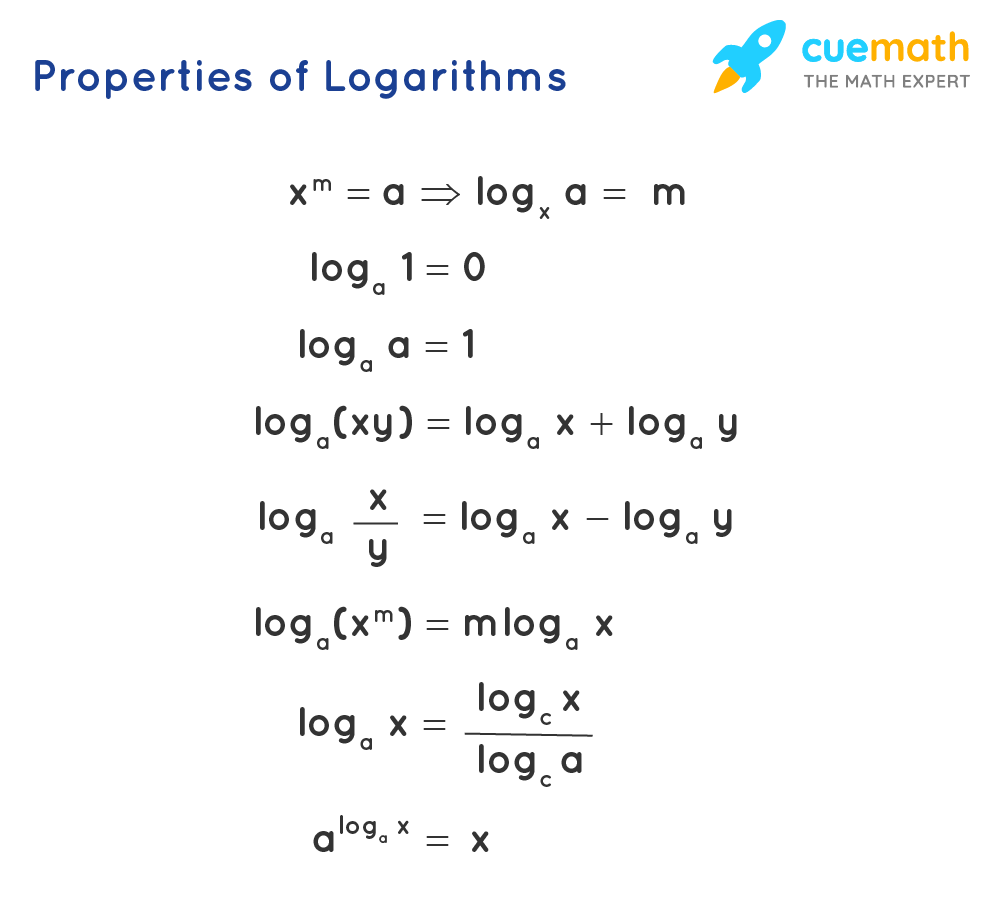
The important log algebraic formulas that we use most commonly are:

• log_a (xy) = log_a x + log_a y
• log_a (x/y) = log_a x - log_a y
• log_a x^m = m log_a x
• log_a a = 1
• log_a 1 = 0

An important algebra formula introduced in class 10 is the “quadratic formula”. The general form of the quadratic equation is ax² + bx + c = 0, and there are two methods of solving this quadratic equation. The first method is to solve the quadratic equation by the algebraic method, and the second method is to solve it through the use of the quadratic formula. The below formula is helpful to quickly find the values of the variable x with the least number of steps.

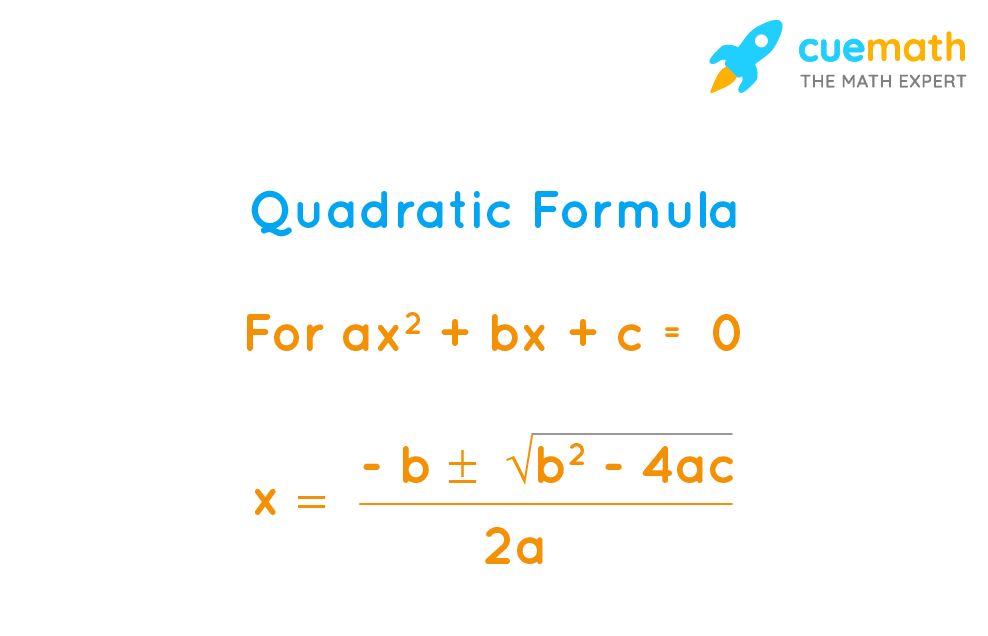
In the above expression, the value b² - 4ac is called the discriminant and is useful to find the nature of the roots of the given equation. Based on the value of the determinant, the three types of roots are given below.

• If b² - 4ac > 0, then the quadratic equation has two distinct real roots.
• If b² - 4ac = 0, then the quadratic equation has two equal real roots.
• If b² - 4ac < 0, then the quadratic equation has two imaginary roots.

Apart from this, we have a few other formulas related to progressions. Progressions include some of the basic sequences such as arithmetic sequence and geometric sequence. The arithmetic sequence is obtained by adding a constant value to the successive terms of the series. The terms of the arithmetic sequence is a, a + d, a + 2d, a + 3d, a + 4d, .... a + (n - 1)d. The geometric sequence is obtained by multiplying a constant value to the successive terms of the series. The terms of the geometric sequence are a, ar, ar², ar³, ar⁴, .....ar^n-1. The below formulas are helpful to find the nth term and the sum of the terms of the arithmetic, and geometric sequence.

Arithmetic Sequence Formulas:

For any arithmetic sequence a, a + d, a + 2d, ...

• n^th term, a_n = a + (n - 1) d
• Sum of the first n terms, S_n = n/2 [2a + (n - 1) d]

Geometric Sequence Formulas:

For any geometric sequence a, ar, ar², ...

• n^th term, a_n = a r^{n - 1}
• Sum of the first n terms, S_n = a (1 - rⁿ) / (1 - r)
• Sum of infinite terms, S = a / (1 - r)

The important topics of Class 11 which have extensive use of algebraic formulas are permutations and combinations. Permutations help in finding the different arrangements of r things from the n available things, and combinations help in finding the different groups of r things from the available n things. The following formulas help in finding the permutations and combination values.

• Permutation Formulas:
  Factorial formula: n! = n × (n - 1) × (n - 2) × ... × 3 × 2 × 1 and
  nPr Formula: ⁿ P _r (or) _n P _r = n! / (n - r)!
• Combination Formula (or) nCr Formula: ⁿ C _r (or) _n C _r = n!/[r!(n−r)!]

Apart from the permutations and combinations, there is another important topic of “Binomial Theorem” as well which is used to evaluate the large exponents of algebraic expressions with two terms. Here the coefficients of the binomial terms are calculated from the formula of combinations. The below expression provides the complete formula for binomial expansion, and it can be termed the algebraic expression of the binomial theorem.

Using this binomial expansion formula, we can simplify complex expansions like (x + 2y)⁷, (3x - y)¹¹, etc.

The vector algebra formulas that are involved in class 12 are as follows.

For any three vectors, a, b and c:

• The magnitude of a = x i+y j+z k is, |a| =√(x²+y²+z²).
• The unit vector along a is a/|a|.
• The dot product is defined as: a ⋅ b = |a| |b| cos θ, where θ is the angle between the vectors a and b.
• The cross product is defined as: a × b = |a| |b| sin θ\(\hat{n}\), where θ is the angle between the vectors a and b.
• The scalar triple product of three vectors is given by [a b c ] = a ⋅ (b × c) = (a × b) ⋅ c.

An algebraic function is of the form y=f(x). Here, x is the input and y is the output of this function. Here, each input corresponds to exactly one output. But multiple inputs may correspond to a single output. For example: f(x) = x² is an algebraic function. Here, when x = 2, f(2) = 2² =4. Here, x = 2 is the input, and f(2) = 4 is the output of the function.

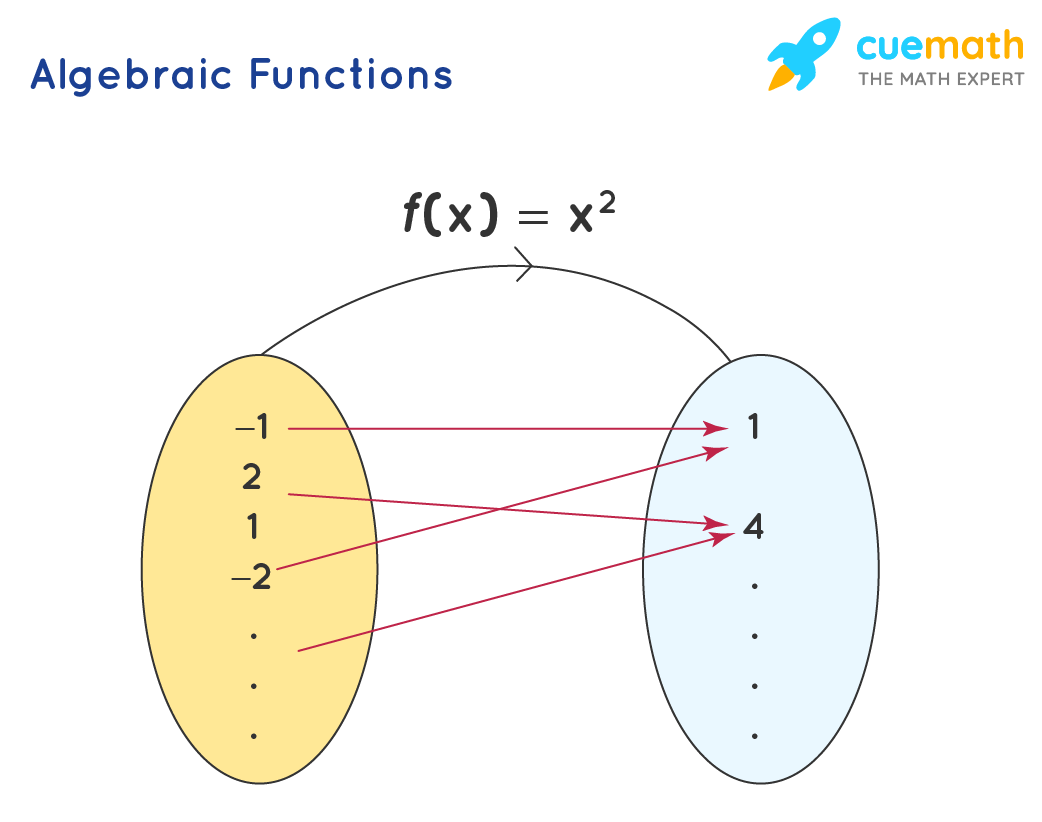
The set of all inputs of a function is known as domain and the set of all the outputs is known as the range. To know more about domain and range, click here.

The fractions in algebra are known as rational expressions. We can perform numerous arithmetic operations such as addition, subtraction, multiplication, and the dividing of fractions in algebra just the same way we do with fractions involving numbers. Further, it only has the unknown variables and involved the same rules of working across fractions. The below four expressions are useful for working with algebraic fractions.

• Adding Fractions: x/y + z/w = (x.w + y.z)/(y.w)
• Subtracting Fractions: x/y - z/w = (x.w - y.z)/(y.w)
• Multiplying Fractions: x/y × z/w = xz/yw
• Dividing Fractions: x/y ÷ z/w = x/y × w/z = xw/yz

Challenging Questions on Algebra Formulas:

Now having understood the concepts of algebraic expression, check out the below three questions to better practice the learned concept.

• Find the roots of the quadratic equation: x²+7x+12=0
• Simplify the expression: (x^-9y³)/(x^-7y⁸) so that the answer has no negative exponents.
• Expand the logarithm: log x²y³ z.

☛Related Articles:

• Algebraic Formula Calculator
• Algebra Calculator
• Math Formulas

 

What are all Algebra Formulas in Math?

Here are some of the most commonly used formulas of algebra:

• a² - b² = (a - b)(a + b)
• (a + b)² = a² + 2ab + b²
• (a - b)² = a² - 2ab + b²
• (x + a)(x + b) = x² + x(a + b) + a b
• (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
• (a + b)³ = a³ + 3a²b + 3ab² + b³
• (a - b)³ = a³ - 3a²b + 3ab² - b³
• a³ - b³ = (a - b)(a² + ab + b²)
• a³ + b³ = (a + b)(a² - ab + b²)

Further, there are algebraic formulas for other topics of maths such as exponents, logarithms, permutations, sequences, and vector algebra. For a detailed list of formulas, scroll up this page.

How do I Learn Algebra Formulas?

Algebra formulas can be easily memorized by visualizing the formulas as squares or rectangles. Further, the understanding of the factorized forms of the formulas helps to easily learn and remember the algebraic formulas.

How to Solve Algebra Formulas?

The solving of algebra equations is aimed at equalizing the left-hand side of the expression with the right-hand side of the expression. Further, the terms can be transferred from the left to the right side of the expression, based on the formulas of algebra.

What Is The Formula For a^2 - b^2 in Algebra Formulas?

The formula for a²- b² is (a+b)(a-b)= a²- b². It is called the difference of squares formula.

What are the Algebra Formulas for Triangular Numbers?

The algebra formula for triangular numbers is H² = B² + A² and it helps to relate the length of the sides of the triangle. It is applicable for a right triangle and has been derived from the Pythagoras theorem. The alphabets H represents the hypotenuse, B represents the base of the right triangle, and A represents the altitude of the triangle. Applying this same formula an example of triangular numbers is (6, 8, 10).

What is the Basis Of Algebra Formulas?

The basis of algebra formulas is that the resultant numeric value of the expressions on either side of the equals to sign is equal. Further, algebraically the terms are modified on either side to match up with the algebraic formulas.

What are Algebra Expressions?

For each of the algebra formulas, the equations with variables, powers, and arithmetic operations, and on either side of the equals to sign are called algebraic expressions/variable expressions. In the algebraic formula (a+b)(a-b)= a²- b², the terms on either side of the equals to sign are called algebraic expressions.

What Are the Applications of Algebraic Expressions Formulas?

The algebraic expression formulas are used to simplify complex algebraic expressions such as (3x + 4y)², (a - 3b + 2c)², etc. Some of these formulas are also used to factorize the polynomials.

What Are Algebraic Expressions Formulas?

The algebraic expression formulas are formulas that are used to simplify the algebraic expressions. Some important algebraic expressions formulas used for expansion are:

• (x + y)² = x² + 2xy + y²
• (x - y)² = x² - 2xy + y²
• (x + y)³ = x³ + y³ + 3xy (x + y)
• (x - y)³ = x³ - y³ - 3xy (x - y)
• (x + y + z)² = x² + y² + z² + 2xy + 2yz + 2zx

Some of the algebraic formulas used for factorization are:

• x² - y² = (x + y) (x - y)
• x³ + y³ = (x + y) (x² – xy + y²)
• x³ - y³ = (x - y) (x² + xy + y²)

How To Derive the Algebraic Expressions Formula (x + y)³ = x³ + y³ + 3xy (x + y)?

We can derive this formula just by multiplying polynomials. Let us start with the left-hand side of this formula and reach the right-hand side at the end.

(x + y)³ = (x + y)² (x + y)

= (x² + 2xy + y²) (x + y)

= x³ + 2x²y + xy² + x²y + 2xy² + y³

= x³ + y³ + 3x²y + 3xy² (or)

= x³ + y³ + 3xy (x + y)

How to Use Algebraic Expressions Formulas While Solving Problems?

We have multiple algebraic expressions formulas and some of them have to be used according to the need while solving the problems. For example, to factorize the expression, 8x³ + 27, we apply the a³ + b³ formula as follows.

a³ + b³ = (a + b) (a² - ab + b²)

Substitute a = 2x and b = 3 on both sides,

(2x)³ + 3³ = (2x + 3) ( (2x)² - (2x)(3) + 3²)

8x³ + 27 = (2x + 3) (4x² - 6x + 9).