Sum of n Terms of an AP

In the 19^th century in Germany, a Math class for grade 10 was going on.

The teacher asked her students to sum all the numbers from \(1\) up to \(100\).

The students were struggling to calculate the sum of all these numbers.

One boy shouted out the answer \(5050\) while the other students were still in the initial steps of calculating the sum.

This boy was the great German mathematician Carl Friedrich Gauss.

How did he arrive at the sum so quickly? 

Well, he noticed that terms equidistant from the beginning and the end of the series had a constant sum equal to \(101\).

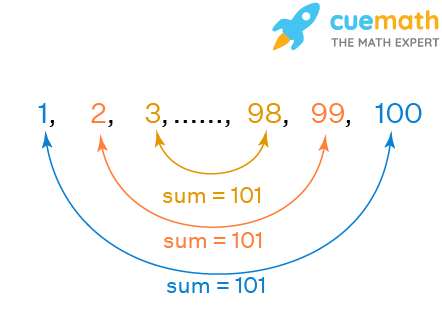
We can see that in the sequence \(1,2,3,...,100\), there are \(50\) such pairs whose sum is \(101\).

Thus, the sum of all terms of this sequence is:

\[ 50 \times 101 = 5050\]

---

Consider an arithmetic progression (AP) whose first term is \(a_1\) (or) \(a\) and the common difference is \(d\).

• The sum of the first \(n\) terms of an arithmetic progression when the \(n^{th} \) term is NOT known is:

\[ S_n=\frac{n}{2}[2 a+(n-1) d] \]

• The sum of the first \(n\) terms of an arithmetic progression when the \(n^{th} \) term, \(a_n\) is known is:

\[ S_n=\frac{n}{2}[a_1+a_n] \]

How do we derive these formulas?

We will use the same logic used above by Carl Friedrich Gauss.

Let us consider the arithmetic progression with \(n\) terms:

\[a,a+d,a+2d,...(a+(n-2) d),(a+(n-1) d)\]

The sum of \(n\) terms of this progression is:

\[ S_n=a+(a+d)+\ldots+(a+(n-2) d)+(a+(n-1) d) \,\,\,\,\,\, \rightarrow (1)  \]

By reversing the order of the terms of this equation:

\[ S_n=(a+(n-1) d)+(a+(n-2) d)+\ldots+(a+d)+a \,\,\,\,\,\, \rightarrow (2)  \]

We see that the sum of corresponding terms of equation (1) and equation (2) yield the same sum which is \(2a+(n-1)d\).

We know that there are totally \(n\) terms in the above AP.

So by adding (1) and (2), we get:

\[  \begin{align}
2S_n &= n(2a+(n-1) d)\\[0.3cm]
S_n &= \frac{n}{2}(2a+(n-1)d)
\end{align} \]

The above sum of arithmetic progression equation can be written as:

\[  \begin{align}
S_n &= \frac{n}{2}(2a+(n-1)d)\\[0.3cm]
S_n &= \frac{n}{2}(a+a+(n-1)d)\\[0.3cm]
S_n &= \frac{n}{2}(a_1+a_n)  [\because a_n=a+(n-1)d \text{   and   } a=a_1 ]
\end{align} \]

Thus, the sum of arithmetic progression equations are:

\(\begin{align} S_n &= \frac{n}{2}(2a+(n-1)d)\\[0.3cm] S_n &= \frac{n}{2}(a_1+a_n)  \end{align} \)

Let's take a look at the following flowchart to get an idea of the formula that has to be used to find the sum of arithmetic progression according to the information available to us.

---

The AP of natural numbers is:

\[1,2,3,...,n,...\]

Let us find the sum of \(n\) terms of AP of natural numbers.

It would be:

\[1+2+3+...+n\]

We can find the sum in two methods using the above two formulas.

Method 1

Here,

The first term is, \(a=1\).

The common difference is, \(d=1\).

The number of terms is \(n\).

Substitute all these values in the first sum of AP formula:

\[\begin{align}
S_n &= \frac{n}{2}(2a+(n-1)d)\\[0.3cm]
S_n &= \frac{n}{2}(2(1)+(n-1)1) \\[0.3cm]
S_n&= \frac{n}{2}(2+n-1)\\[0.3cm]
S_n&= \frac{n(n+1)}{2}
\end{align} \]

Method 2

Here,

The first term is, \(a_1=1\).

The nth term of the above AP is, \(a_n=n\).

Substitute all these values in the second sum of AP formula:

\[\begin{align}
S_n &= \frac{n}{2}(a_1+a_n)\\[0.3cm]
S_n&=  \frac{n}{2} (1+n)\\[0.3cm]
S_n&= \frac{n(n+1)}{2}
\end{align} \]

Thus, from the above methods, the sum of AP of natural numbers is:

Sum of AP of natural numbers \(  = \dfrac{n(n+1)}{2} \)

---

Let us consider an example for the sum of an infinite AP.

\[ 2+ 5 + 8+... \]

Here, the first term is, \(a=2\).

The common difference is, \(d=3\).

The number of terms is, \(n= \infty\).

Substitute all these values in the formula of sum of AP: 

\[\begin{align}
S_n &= \frac{n}{2}(2a+(n-1)d)\\[0.3cm]
S_n &= \frac{\infty}{2}(2(2)+(\infty-1)3) \\[0.3cm]
S_n&= \infty
\end{align} \]

We found the sum of infinite AP to be \(\infty\) when

\(d>0\).

In the same way, the sum of infinite AP is \(-\infty\) when

\(d<0\).

Thus,

\(\text { Sum of infinite } A P=\left\{\begin{array}{ll} \infty, & \text { if } \quad d>0 \\[0.3cm] -\infty, & \text { if } \quad d<0 \end{array}\right.  \)