Arithmetic Progression
An arithmetic progression (AP) is a sequence where the differences between every two consecutive terms are the same. For example, the sequence 2, 6, 10, 14, … is an arithmetic progression (AP) because it follows a pattern where each number is obtained by adding 4 to the previous term. A real-life example of an AP is the sequence formed by the annual income of an employee whose income increases by a fixed amount of $5000 every year.
In this article, we will explore the concept of arithmetic progression, the AP formulas to find its nth term, common difference, and the sum of n terms of an AP. We will solve various examples based on the arithmetic progression formula for a better understanding of the concept.
What is Arithmetic Progression?
An arithmetic progression (AP) is a sequence of numbers where the differences between every two consecutive terms are the same. In this progression, each term, except the first term, is obtained by adding a fixed number to its previous term. This fixed number is known as the common difference and is denoted by 'd'. The first term of an arithmetic progression is usually denoted by 'a' or 'a1'.
For example, 1, 5, 9, 13, 17, 21, 25, 29, 33, ... is an arithmetic progression as the differences between every two consecutive terms are the same (as 4). i.e., 5 - 1 = 9 - 5 = 13 - 9 = 17 - 13 = 21 - 17 = 25 - 21 = 29 - 25 = 33 - 29 = ... = 4. We can also notice that every term (except the first term) of this AP is obtained by adding 4 to its previous term. In this arithmetic progression:
- a = 1 (the first term)
- d = 4 (the "common difference" between terms)
Thus, an arithmetic progression, in general, can be written as: {a, a + d, a + 2d, a + 3d, ... }.
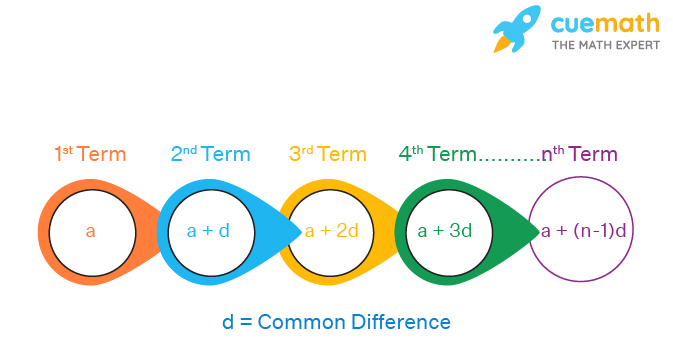
In the above example we have: {a, a + d, a + 2d, a + 3d, ... } = {1, 1 + 4, 1 + 2 × 4, 1 + 3 × 4, ... } = {1, 5, 9, 13, ... }
Arithmetic Progression Formula (AP Formulas)
For the first term 'a' of an AP and common difference 'd', given below is a list of arithmetic progression formulas that are commonly used to solve various problems related to AP:
- Common difference of an AP: d = a2 - a1 = a3 - a2 = a4 - a3 = ... = an - an-1
- nth term of an AP: an = a + (n - 1)d
- Sum of n terms of an AP: Sn = n/2 (2a + (n - 1) d) = n/2 (a + l), where l is the last term of the arithmetic progression.
The following image comprehends all AP formulas.

Common Terms Used in Arithmetic Progression
From now on, we will abbreviate arithmetic progression as AP. An AP generally is shown as follows: a1, a2, a3, . . . It involves the following terminology.
First Term of Arithmetic Progression:
As the name suggests, the first term of an AP is the first number of the progression. It is usually represented by a1 (or) a. For example, in the sequence 6, 13, 20, 27, 34, . . . . the first term is 6. i.e., a1 = 6 (or) a = 6.
Common Difference of Arithmetic Progression:
We know that an AP is a sequence where each term, except the first term, is obtained by adding a fixed number to its previous term. Here, the “fixed number” is called the “common difference” and is denoted by 'd' i.e., if the first term is a1, then: the second term is a1+ d, the third term is a1+ d + d = a1 + 2d, and the fourth term is a1 + 2d + d= a1+ 3d and so on. For example, in the sequence 6, 13, 20, 27, 34,. . . , each term, except the first term, is obtained by the addition of 7 to its previous term. Thus, the common difference is, d=7. In general, the common difference is the difference between every two successive terms of an AP. Thus, the formula for calculating the common difference of an AP is: d = an - an-1.
Here are some AP examples with their first term and common difference.
- 6, 13, 20, 27, 34, . . . . is an AP with the first term 6 and common difference 7.
- 91, 81, 71, 61, 51, . . . . is an AP with the first term 91 and common difference -10.
- π, 2π, 3π, 4π, 5π,… is an AP with the first term π and common difference π.
- -√3, −2√3, −3√3, −4√3, −5√3,… is an AP with the first term -√3 and common difference -√3.
Nth Term of Arithmetic Progression
The general term (or) nth term of an AP whose first term is 'a' and the common difference is 'd' is given by the formula an = a + (n - 1) d. For example, to find the general term (or) nth term of the progression 6, 13, 20, 27, 34,. . . ., we substitute the first term, a1 = 6, and the common difference, d = 7 in the formula for the nth term formula. Then we get, an = a + (n - 1) d = 6 + (n - 1) 7 = 6 + 7n - 7 = 7n -1. Thus, the general term (or) nth term of this AP is: an = 7n - 1. But what is the use of finding the general term of an AP? Let us see.
Use of AP Formula for General Term
We know that to find a term, we can add 'd' to its previous term. For example, if we have to find the 6th term of 6, 13, 20, 27, 34, . . ., we can just add d = 7 to the 5th term which is 34. Then 6th term = 5th term + 7 = 34 + 7 = 41. But what if we have to find the 102nd term? Isn’t it difficult to calculate it manually? In this case, we can just substitute n = 102 (and also a = 6 and d = 7 in the formula of the nth term of an AP). Then we get:
an = a + (n - 1) d
a102 = 6 + (102 - 1) 7 = 6 + (101) 7 = 713
Therefore, the 102nd term of the given AP 6, 13, 20, 27, 34, .... is 713. Thus, the general term (or) nth term of an AP is referred to as the arithmetic sequence explicit formula and can be used to find any term of the AP without finding its previous term.
The following table shows some AP examples and the first term, the common difference, and the general term in each case.
| Arithmetic Progression | First Term | Common Difference |
General Term (nth term) |
|---|---|---|---|
| AP | a | d | an= a + (n-1)d |
| 91, 81, 71, 61, 51, . . . | 91 | -10 | -10n + 101 |
| π, 2π, 3π, 4π, 5π,… | π | π | πn |
|
–√3, −2√3, −3√3, −4√3–,… |
-√3 | -√3 | -√3 n |
Sum of Arithmetic Progression
Consider an arithmetic progression (AP) whose first term is a1 (or) a and the common difference is d.
- The sum of first n terms of an arithmetic progression when the nth term is NOT known is Sn = (n/2) [2a + (n - 1) d]
- The sum of first n terms of an arithmetic progression when the nth term(an) is known is Sn = n/2[a1 + an]
Example: Mr. Kevin earns $400,000 per annum and his salary increases by $50,000 per annum. Then how much does he earn at the end of the first 3 years?
Solution: The amount earned by Mr. Kevin for the first year is, a = 4,00,000. The increment per annum is, d = 50,000. We have to calculate his earnings in the 3 years. So n = 3.
Substituting these values in the AP sum formula,
Sn = n/2 [2a + (n - 1) d]
Sn= 3/2(2(400000) + (3 - 1)(50000))
= 3/2 (800000 + 100000)
= 3/2 (900000)
= 1350000
He earned $1,350,000 in 3 years.
We can get the same answer by general thinking also as follows: The amount earned in 3 years = 400000 + 450000 + 500000 = 1350000. This could be calculated manually as n is a smaller value. But the above formulas are useful when n is a larger value.
Derivation of AP Sum Formula
Let us consider the first n terms of an arithmetic progression a1, a1 + d, a1 + 2d, ...., a1 + (n - 1) d. Assume that the sum of these n terms is Sn. Then
Sn = a1 + (a1 + d) + (a1 + 2d) + … + [a1 + (n–1)d].
We can also start with the nth term and successively subtract the common difference, so,
Sn = an + (an – d) + (an – 2d) + … + [an – (n–1)d].
Thus the sum of the arithmetic progression could be found in either of the ways. However, on adding those two equations together, we get
Sn = a1 + (a1 + d) + (a1 + 2d) + … + [a1 + (n–1)d]
Sn = an + (an – d) + (an – 2d) + … + [an – (n–1)d]
_________________________________________
2Sn = (a1 + an) + (a1 + an) + (a1 + an) + … + (a1 + an).
____________________________________________
Notice all the d terms are cancelled out. So,
2Sn = n (a1 + an)
⇒ Sn = [n(a1 + an)]/2 --- (1)
By substituting an = a1 + (n – 1)d into the last formula, we have
Sn = n/2 [a1 + a1 + (n – 1)d] ...Simplifying
Sn = n/2 [2a1 + (n – 1)d] --- (2)
These two formulas (1) and (2) help us to find the sum of an arithmetic series quickly.
Differences Between Arithmetic Progression and Geometric Progression
The following table explains the differences between arithmetic and geometric progression:
| Property | Arithmetic progression | Geometric progression |
|---|---|---|
| Definition |
It is a sequence in which the difference between every two consecutive terms is constant. |
It is a sequence in which the ratio of every two consecutive terms is constant. |
| Common Difference/Ratio | d | r |
| General form | a, a + d, a + 2d, a + 3d, ... | a, ar, ar2, ar3, ... |
| nth term formula | a + (n - 1) d | a rn - 1 |
| Sum of n terms formula | n/2 [2a + (n – 1)d] | (a(rn - 1)) / (r - 1) |
| How the terms vary? | The consecutive terms vary linearly. | The consecutive terms vary exponentially. |
Important Notes on Arithmetic Progression:
- An AP is a list of numbers in which each term is obtained by adding a fixed number to the preceding number.
- a is represented as the first term, d is a common difference, an as the nth term, and n as the number of terms.
- In general, AP can be represented as a, a + d, a + 2d, a + 3d, ...
- The nth term of an AP can be obtained by an = a + (n − 1)d
- The sum of an AP can be obtained by sn= n/2 [2a + (n − 1) d]
- The graph of an AP is a straight line with the slope as the common difference.
- The common difference doesn't need to be positive always. For example, in the progression, 16, 8, 0, −8, −16, ... the common difference is negative (d = 8 - 16 = 0 - 8 = -8 - 0 = -16 - (-8) =... = -8).
☛ Related Articles:
Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12. Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.
Arithmetic Progression Examples
-
Example 1: Find the general term of the arithmetic progression -3, -(1/2), 2…
Solution:
The given progression is -3, -(1/2),2…
Here, the first term is a = -3, and the common difference is, d = -(1/2) - (-3) = -(1/2) + 3 = 5/2
By AP formulas, the general term of an AP is calculated by the formula:
an = a + (n - 1) d
an = -3 + (n - 1) 5/2
= -3 + (5/2)n - 5/2
= 5n/2 - 11/2
Therefore, the general term of the given AP is:
Answer: an = 5n/2 - 11/2
-
Example 2: Which term of the AP 3, 8, 13, 18,... is 78?
Solution:
The given progression is 3,8,13,18,...
Here the first term is a = 3, and the common difference is, d = 8 - 3= 13 - 8 = ... = 5
Let us assume that the nth term is,
an = 78
Substitute all these values in the general term of an arithmetic progression:
an = a+(n - 1)d
78 = 3 +(n - 1)5
78 = 3 + 5n - 5
78 = 5n - 2
80 = 5n
16 = n
Answer: ∴ 78 is the 16th term.
-
Example 3: Find the sum of the first 5 terms of the arithmetic progression whose first term is 3 and 5th term is 11.
Solution: We have a1 = a = 3 and a5 = 11 and n = 5.
Using the AP formula for the sum of n terms, we have
Sn = (n/2) (a + an)
⇒ S5 = (5/2) (3 + 11)
= (5/2) × 14
= 35
Answer: The required sum of the first 5 terms is 35.

FAQs on Arithmetic Progression
What is the Meaning of Arithmetic Progression in Maths?
A sequence of numbers where each term (other than the first term) is obtained by adding a fixed number to its previous term is called an arithmetic progression (A.P.). For example, is 3, 6, 9, 12, 15, 18, 21, … is an A.P. In simple words, we can say that an arithmetic progression is a sequence of numbers where the difference between each consecutive term is the same.
What is AP formula?
Here are the AP formulas corresponding to the AP a, a + d, a + 2d, a + 3d, . . . a + (n - 1)d:
- The formula to find the nth term is: an = a + (n – 1) × d
- The formula to find the sum of n terms is Sn = n/2 [2a + (n − 1) × d]
What are the Explicit Formula and Recursive Formula of AP?
For an AP a, a + d, a + 2d, ...
- the explicit formula to find the nth term is, an = a + (n - 1) d
- the recursive formula to find the nth term is, an = an - 1 + d
How to Find the Sum of Arithmetic Progression?
To find the sum of arithmetic progression, we have to know the first term (a), the number of terms(n), and the common difference (d) between consecutive terms. Then substitute the values in the formula Sn = n/2[2a + (n − 1) × d].
How to Find Number of Terms in Arithmetic Progression?
The number of terms in an arithmetic progression can be simply found by the division of the difference between the last and first terms by the common difference, and then adding 1.
What is the Sum of N Terms of the Arithmetic Progression Formula?
The sum of first n terms of an arithmetic progression can be calculated using one of the following two formulas:
- Sn = n/2 [2a + (n - 1)d]
- Sn = n/2 [a1 + an].
How to Find Common Difference in Arithmetic Progression?
The common difference is the difference between every two consecutive terms in an arithmetic progression. Therefore, you can say that the formula to find the common difference of an arithmetic sequence is: d = an - an - 1, where an is the nth term in the progression, and an - 1 is the previous term.
How to Find First Term in Arithmetic Progression?
If we know ‘d'(common difference) and any term (nth term) in the progression then we can find ‘a' (first term). If 5th term is 10 and d = 2, then a5= a + 4d; 10 = a + 4(2); 10 = a + 8; a = 2.
What is the Difference Between Arithmetic Series and Arithmetic Progression?
Arithmetic progression is a progression in which the difference between every two consecutive terms is a constant whereas an arithmetic series is the sum of the elements of Arithmetic Progression.
What are the Types of Progressions in Maths?
There are three types of progressions in Maths. They are:
- Arithmetic Progression (AP)
- Geometric Progression (GP)
- Harmonic Progression (HP)
How do you Solve Arithmetic Progression Problems?
The following formulas help to solve arithmetic progression problems:
- Common difference of an AP: d = an - an-1.
- nth term of an AP: an = a + (n - 1)d
- Sum of n terms of an AP: Sn = n/2 (2a + (n - 1)d)
Where is Arithmetic Progression Used?
A real-life application of arithmetic progression is seen when you take a taxi. Once you ride a taxi you will be charged an initial rate and then a per-mile or per-kilometre charge. This shows an arithmetic progression that for every kilometre you will be charged a certain fixed (constant) rate plus the initial rate.
What is Infinite Arithmetic Progression?
When the number of terms in an AP is infinite, we call it an infinite arithmetic progression. For example, 2, 4, 6, 8, 10, ... is an infinite AP; etc. The sum of an infinite arithmetic progression doesn't exist.
What is Nth Term in Arithmetic Progression?
The 'nth' term in an AP is a formula with 'n' in it which enables you to find any term of a progression without having to go up from one term to the next. 'n' stands for the term number so to find the 50th term we would just substitute 50 in the formula an = a+ (n - 1)d in place of 'n'.
How to Find d in Arithmetic Progression?
To find d in an arithmetic progression, we take the difference between any two consecutive terms of the AP. It is always a term minus its previous term. An alternative way to find the common difference is just to see how much each term is getting added to get the next term.
visual curriculum