Imaginary Numbers
A Greek mathematician called Hero of Alexandria first invented imaginary numbers. Later in 1572, an Italian mathematician Gerolamo Cardano developed the rules for multiplying imaginary numbers. These numbers are helpful in finding the square roots of negative numbers.
Let us learn more about imaginary numbers along with their definition, examples, and geometrical interpretation. Also, let us see how to do calculations on these numbers.
| 1. | What are Imaginary Numbers? |
| 2. | Geometrical Interpretation of Imaginary Numbers |
| 3. | i in Math |
| 4. | Calculating Imaginary Numbers |
| 5. | Tips and Tricks on Imaginary Numbers |
| 6. | FAQs on Imaginary Numbers |
What are Imaginary Numbers?
Imaginary numbers are numbers that result in a negative number when squared. They are also defined as the square root of negative numbers. An imaginary number is the product of a non-zero real number and the imaginary unit "i" (which is also known as "iota"), where i = √(-1) (or) i2 = -1.
Let's try squaring some real numbers:
(−2)2 = −2×−2 = 4
52 = 5×5 = 25
(1.3)2 = 1.3×1.3 = 1.69
Is any of the results a negative number? No. It means the square of any real number is always positive. Then what number results in a negative square? It is an imaginary number. In math, we come across the square root of negative numbers many times, especially in the case of solving quadratic equations using the quadratic formula. In such cases, the usage of imaginary numbers is mandatory. Here are some imaginary numbers examples:
- √(-4) = √(-1) · √4 = i (2) = 2i
- √(-3) = √(-1) · √3 = i √3
In the above examples, 2i and i √3 are imaginary numbers. We can see that each of these numbers is a product of a non-zero real number and i. Thus, we can derive a rule for imaginary numbers which is:
- √(-x) = i √x
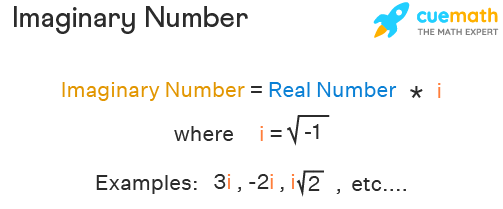
These are a part of complex numbers, where a complex number is the sum of a real number and an imaginary number. i.e., a complex number is of the form a + ib, where both 'a' and 'b' are real numbers and here bi is an imaginary number.
Geometrical Interpretation of Imaginary Numbers
We usually represent a complex number a+bi by a point (a, b) in the Argand plane. For example, a complex number 1-3i represents the point (1, -3) on the Argand plane. So an imaginary number bi (which can be written as 0 + bi) represents a point (0, b) on the plane and hence it is a point on the vertical axis (imaginary axis). Thus, the imaginary numbers always lie on the vertical axis of an Argand plane. Here are a few examples.

i in Math
What exactly is the term i in the complex number x+iyx+iy corresponding to the point P(x, y)? Clearly, "i" cannot be a real number, because if i was real, then x+iyx+iy would also be real, and would lie on the real axis itself. Thus, if i was real, then x+iy would only represent points on the real axis, rather than points in a plane.
If we want to represent points in a plane using numbers, i must be a non-real number, in the sense that it must not lie in the Real set. We interpret i in math as follows: "i is one unit in the direction perpendicular to the real axis". In the above figure, we can see that the point (0, 1) is nothing but "i".
Thus, in the complex number x+iy, the term iy becomes a non-real number: it represents y times i, that is, y units in the i direction. Hence x+iy represents a point that can be reached by moving x units in the Real direction and y units in the i direction (from the origin):

Value of i
It turns out that arithmetically, i2=−1. In other words, the value of i is the square root of −1. For now, don’t ask how! As we said earlier, the various different parts of the puzzle that is Complex Numbers will fall into place as you delve deeper into this subject.
At this point, just keep in mind that:
-
i is a non-real number (it lies outside the Real set).
-
i represents one unit perpendicular to the Real direction.
-
yi represents y units perpendicular to the Real direction
-
x+iy represents the point (x, y)
-
i is the square root of −1, or, i2=−1.
When we say that i is a non-real number, we do not mean that i does not exist or is a figment of our imagination. We mean to say that i is non-real in the sense that it does not like in the Real set. However, it is a perfectly valid mathematical entity. i is also known by the name "iota".
Calculating Imaginary Numbers
We can do all calculations on imaginary numbers also just like how we do with real numbers. Let us see how we do them.
Adding/Subtracting Imaginary Numbers
Adding or subtracting imaginary numbers is just like how we combine the like terms in algebra. For example:
- 2i + 3i = 5i
- 2i - 3i = -i
Multiplying Imaginary Numbers
We multiply the imaginary numbers just like how we multiply the terms in algebra. Here, we may have to use the rule of exponents am × an = am+n. But here, we have to take care of the fact that i2 = -1. Here are some examples.
- 2i × 3i = 6i2 = 6(-1) = -6
- 3i2 × -5i3 = -15i5 = -15 (i2)2 i = -15 (-1)2 i = -15i
We may feel that simplifying the powers of iota is difficult. Here are some rules that make the process of finding powers of "i" easier while multiplying complex numbers.
- i4k = 1
- i4k+1 = 1
- i4k+2 = -1
- i4k+3 = -i
where k is a whole number. These rules state that "i" raised to a number is equal to the "i" raised to the number which is the remainder obtained by dividing the original number by 4. For example:
- i4 = i0 = 1
- i17 = i1 = i
Any power of i is equal to one of 1, i, -i, and -1 after simplification. We can understand this from the figure below.

These rules really made calculating the product of imaginary numbers very easy.
Dividing Imaginary Numbers
While dividing imaginary rules, we use the rule of exponents am / an = am-n. In the result after division, we usually do not keep "i" in the denominator. If we get so, then we use the rule 1/i = -i (this is because 1/i = 1/i · i/i = i/i2 = i/(-1) = -i). Here are some examples:
- 4i/2i = 2
- 3i3 / 4i6 = 3/(4i3) = 3/(4(i2)(i)) = -3/(4i) = (-3/4)(-i) = 3i/4
Tips and Tricks on Imaginary Numbers
- When the minus sign comes out of the square root, it becomes i because the value of i in math is, i = √(-1).
- \(\sqrt[n]{x}\) can be simplified using the imaginary numbers where x is negative and n is even number.
- When "i" is the denominator (or in case of negative powers of i), use the rule 1/i= -i.
- in = ir, where 'r' is the remainder obtained by dividing n by 4. Then we can apply one of the rules: i2 = -1, i3 = -i, i4 = 1.
Examples on Imaginary Numbers
-
Example 1: Determine the value of (3i)2.
Solution:
(3i)2 = (3i)(3i)
= 9i2
= 9(-1)
= -9
The third step is because by the definition of imaginary numbers i = √(-1) and this means that i2 = -1.
Answer: (3i)2 = -9.
-
Example 2: Express the roots of the quadratic equation x2 + x + 1 = 0 in terms of imaginary numbers.
Solution:
Comparing the given quadratic equation with ax2 + bx + c = 0, we get a = 1, b = 1, and c = 1. Substituting these in the quadratic formula:
x = (-b ± √(b2 - 4ac) ) / (4a)
= (-1 ± √(12 - 4 · 1 · 1) ) / (4·1)
= (-1 ± √(1 - 4) ) / 4
= (-1 ± √(-3) ) / 4
= (-1 ± i√3 ) / 4Answer: The roots are (-1 + i√3 ) / 4 and (-1 - i√3 ) / 4.
-
Example 3: Find the values of (a) i101 and (b) i-199.
Solution:
To simplify this, we use the rule of imaginary numbers which says in = ir, where n is the remainder that is obtained by dividing n by 4.
(a) i101 = i1 = i
(b) i-199 = 1/i199
= 1/i3
= 1/(-i) (because i3 = i2 (i)= (-1)(i) = -i)
= -1/i
= - (-i) (because 1/i = -i)
= iAnswer: (a) i101 = i (b) i-199 = i.

FAQs on Imaginary Numbers
What is Imaginary Numbers Definition?
An imaginary number is a number that is the product of a non-zero real number and the iota "i". Here, i = √(-1) or i2 = -1. These numbers are helpful to find the square root of negative numbers. Some examples of imaginary numbers are -4i, 6i, i, etc.
What is the Value of i in Math?
"i" in math is known as an imaginary unit. Its value is √-1. It is used to calculate the square roots of negative numbers. It is also a part of complex numbers.
What is the Process of Simplifying Imaginary Numbers?
To add/subtract imaginary numbers, we just add/subtract their coefficients. For example, -2i + 8i - 4i = i. We multiply/divide imaginary numbers just like how we do with terms in algebra. But we use the facts i2 = -1 and 1/i = -i while multiplying/dividing imaginary numbers.
What is the Difference Between Imaginary Numbers and Complex Numbers?
An imaginary number is of the form bi whereas a complex number is of the form a+bi where both a and b are real numbers. All imaginary numbers are complex numbers (as 'a' may be 0) but all complex numbers may not be imaginary numbers.
What is the Difference Between Imaginary Numbers and Real Numbers?
A real number can be a natural number, a whole number, an integer, a rational number, or an irrational number. But an imaginary number is the product of a real number and "i" where i = √(-1). We use imaginary numbers to evaluate the square root of negative numbers. For example, √(-9) = √(-1) . √9 = i (3) = 3i.
What are Imaginary Numbers Rules?
Here are some rules that are helpful in calculating imaginary numbers.
- i = √(-1)
- i2 = -1
- i3 = -i
- i4 = 1
- in = ir, where r is the remainder obtained by dividing n by 4.
- 1/i = -i and this rule is helpful for calculating the negative powers of i.
How to Write a Real Number in Terms of i in Math?
Any real number x can be written as x + i0. In other words, a real number can also be thought of as a complex number in which the non-real part is 0. Thus, every real number is a complex number. Put differently, the Real set is a subset of the Complex set. This should be geometrically obvious as well: the Real Line is a subset of the Complex Plane.
What are the Applications of Imaginary Numbers?
- Imaginary numbers are used to simplify the square roots of negative numbers.
- They are used in solving quadratic equations.
- They are used in the formation of complex numbers.
- They are used in physics and in advanced calculus.
Is 0 an Imaginary Number?
Though 0 can be written as 0i, it is not an imaginary number as it is not associated with the square root of any negative number. That is why we clearly mention in the imaginary number definition that it is of the form bi where 'b' is a non-zero real number.
visual curriculum