A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
LearnPracticeDownload

Square root of 289

289 is a perfect square number which is obtained by square of 17. Hence, the square root of 289 is a rational number. In this mini-lesson we will learn to find square root of 289 along with solved examples. Let us see what the square root of 289 is.

  • Square Root of 289: √289 = 17
  • Square of 289: 2892 = 83,521
1. What Is the Square Root of 289?
2. Is Square Root of 289 Rational or Irrational?
3. How to Find the Square Root of 289?
4. FAQs on Square Root of 289

What Is the Square Root of 289?

The original number whose square is 289 gives the square root of 289.

√289 = 17

The answer which we get on squaring 17 is 289. This makes 289 a perfect square.

Is the Square Root of 289 Rational or Irrational?

A rational number can be either terminating or non-terminating and has a repeating pattern in its decimal part. We saw that √289 = 17. 17 is a whole number. It is possible to express it in p/q form easily. Hence, √289 is a rational number.

How to Find the Square Root of 289?

There are different methods to find the square root of any number. Click here to know more about it.
The factors of 289 are, 1, 17 and 289.
As 289 has more than 2 factors, it is a composite number

To find the square root of 289:

  • We can use prime factorization method to obtain one number from each pair of the same numbers and multiply them. The factorization of 289 is 17 × 17 which consists of 1 pair of the same number, 17. Thus, the square root of 289 is √(17 × 17) = 17 itself.

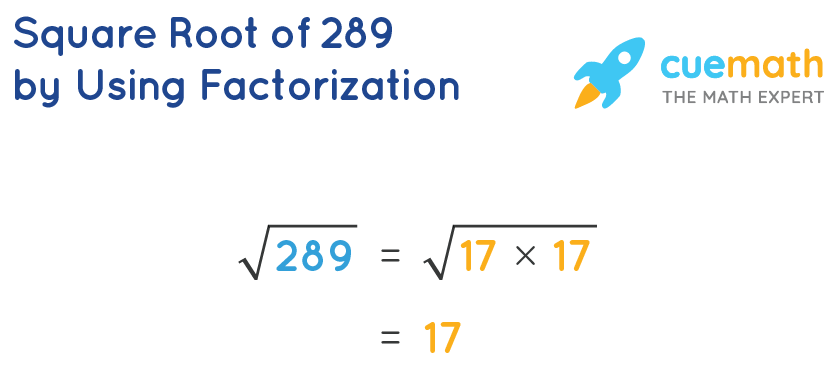
Square Root of 289 Using Factorization

  • Since 289 is a perfect square, we can also express it as 172. The number within square root which gets repeated is 17. Hence, the square root of 289 is 17.

Square Root of 289

The square root of 289 is 17.

Explore Square roots using illustrations and interactive examples

Important Notes:

  • 289 is a perfect square as the answer obtained after square root is a rational number.
  • The square root of 289 can be simplified to 17 either by using the prime factorization of 289 or by expressing 289 as a square of 17.

Think Tank:

  • Can the value of a square root of 289 be decimal?
  • Is √-289 a real number? 
 

Square Root of 289 Solved Examples

  1. Example 1: What is the difference in lengths of square boxes having area 289 square inches and 169 square inches ?

    Solution

    As the area of square box is area = length × length
    The length of square box having area 289 square inches is √289 = 17 inches. 
    Similarly the length of box having area 169 square inches is √169 = 13 inches.
    The difference in lengths of boxes is (17 - 13) inches = 4 inches
    Hence, the difference in length of square boxes having area 289 square inches and 169 square inches is 4 inches.

  2. Example 2: Can you determine the radius of circle having area 289π square inches?

    Solution

    Radius can be found using the formula of area of a circle is πr2 square inches. By the given information,
    πr2 = 289π 
    r2 = 289
    By taking the square root on both sides we get, √r2= √289. We know that the square root of r2 is r.
    By calculating the square root of 289 is 17 inches.

View More >

go to slidego to slide

Breakdown tough concepts through simple visuals.
Math will no longer be a tough subject, especially when you understand the concepts through visualizations.

Book a Free Trial Class

 

FAQs On Square Root of 289

What are the two square roots of 289?

The square roots of 289 are -17 and 17.

Is 289 a perfect square?

Yes, 289 is a perfect square

Does 289 have a square root?

Yes, 289 has a square root

Can square root of 289 simplified?

289 can be broken down as a product of 17 × 17. Either ways, the square root of 289 gives output as 17.

Is the square root of 289 rational or irrational?

The square root of 289 is rational.

Is square root of 289 a real number?

Yes, the square root of 289 is a real number.

Math worksheets and
visual curriculum