A day full of math games & activities. Find one near you.

Square Root of 12

The square root of 12 is expressed as √12 in the radical form and as (12)^½ or (12)^0.5 in the exponent form. The square root of 12 rounded up to 5 decimal places is 3.46410. It is the positive solution of the equation x² = 12. We can express the square root of 12 in its lowest radical form as 2 √3.

Square Root of 12: 3.4641016151377544
Square Root of 12 in exponential form: (12)^½ or (12)^0.5
Square Root of 12 in radical form: √12 or 2 √3

1.	What Is the Square Root of 12?
2.	Is Square Root of 12 Rational or Irrational?
3.	How to Find the Square Root of 12?
4.	Important Notes
5.	FAQs on Square Root of 12
6.	Challenging Questions

What Is the Square Root of 12?

Square root of 12 in the radical form is expressed as √12 and in the exponent form, it is expressed as 12^1/2. Square root of 12 rounded to 5 decimal places is 3.46410. We can also express the square root of 12 in its lowest radical form as 2√3. Numbers which have a radical symbol in their lowest form are called surds.

Is Square Root of 12 Rational or Irrational?

A number which cannot be expressed as a ratio of two integers is an irrational number. The decimal form of the irrational number will be non-terminating (i.e. it never ends) and non-recurring (i.e. the decimal part of the number never repeats a pattern).

Now let us look at the square root of 12.

√12 = 3.4641016151

Do you think the decimal part stops after 3.4641016151? No, it is never-ending and you cannot see a pattern in the decimal part. Thus, √12 is an irrational number.

How to Find the Square Root of 12?

Let us follow the steps to find the square root of 12 by long division.

Step 1: Make a pair of digits (by placing a bar over it) from the unit's place since our number is 12.

Let us represent it inside the division symbol.

Step 2: Find a number such that when you multiply it with itself, the product is less than or equal to 12

We know that 3 × 3 = 9 and 9 is less than 12. Now let us divide 12 by 3.

Step 3: Let us place a decimal point and a pair of zeros next to it and continue our division.

Now, multiply the quotient by 2 and the product becomes the starting digit of our next divisor.

Step 4: Choose a number in the unit's place for the new divisor such that its product with a number is less than or equal to 300.

We know that 6 is in the ten's place and our product has to be 300 and the closest multiplication is 64 × 4 = 256

Step 5: Bring down the next pair of zeros and multiply the quotient 34 (ignore the decimal) by 2, which is 68, and the starting digit of the new divisor.

Step 6: Choose a number in the unit's place for the new divisor such that its product with a number is less than or equal to 4400.

Step 7: Add more pairs of zeros and repeat the process of finding the new divisor and product as in step 2.

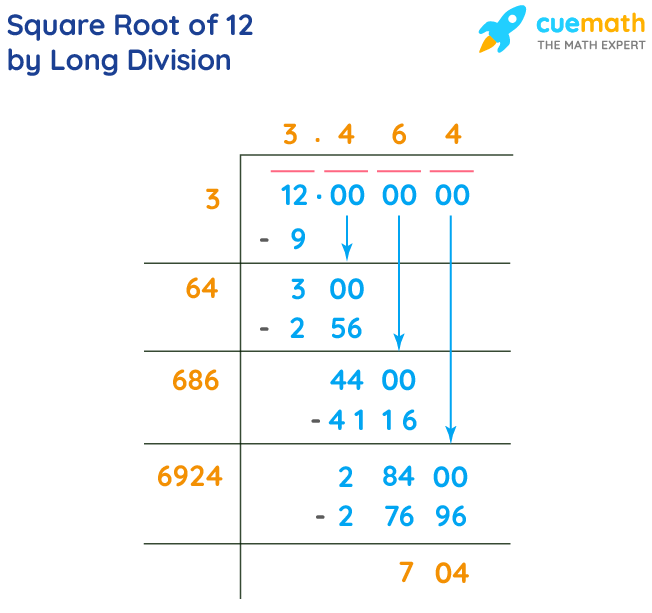
Note that the square root of 12 is an irrational number, i.e., it is never-ending. Hence, we can stop the process after 4 or 5 iterations, and you will get the square root of 12 by the long division method.

Explore square roots using illustrations and interactive examples

Important Notes:

Square root of 12 in the radical form is expressed as √12
In exponent form, square root of 12 is expressed as √12 = 12^1/2.
The real roots of √12 are 3.464...

Challenging Questions:

What is the value of √√√√12
Simplify( (√12)^1/2)^1/2)

Example 1: Tim says that the value of -(√12) is the same as (√-12). What do you think?

Solution

A negative square root cannot have real roots.

-(√12) has real roots but (√-12) has only imaginary roots.

Hence, they are not the same. (√-12) is not the same as (-√12).
Example 2: Help Ryan simplify the square root of 12 to its lowest radical form.

Solution

We need to express 12 as the product of its prime factors.

12 = 3 × 2 × 2

Therefore, √12 = √{ 3 × 2 × 2} = 2√3

Thus, 2√3 is in the lowest radical form.
Example: If the area of a circle is 12π in². Find the radius of the circle.

Solution:

Let 'r' be the radius of the circle.
⇒ Area of the circle = πr² = 12π in²
⇒ r = ±√12 in
Since radius can't be negative,
⇒ r = √12
The square root of 12 is 3.464.
⇒ r = 3.464 in

go to slide go to slide go to slide

Great learning in high school using simple cues

Indulging in rote learning, you are likely to forget concepts. With Cuemath, you will learn visually and be surprised by the outcomes.

Book a Free Trial Class

FAQs on the Square Root of 12

What is the Value of the Square Root of 12?

The square root of 12 is 3.4641.

Why is the Square Root of 12 an Irrational Number?

Upon prime factorizing 12 i.e. 2² × 3¹, 3 is in odd power. Therefore, the square root of 12 is irrational.

What is the Value of 8 square root 12?

The square root of 12 is 3.464. Therefore, 8 √12 = 8 × 3.464 = 27.713.

What is the Square of the Square Root of 12?

The square of the square root of 12 is the number 12 itself i.e. (√12)² = (12)^2/2 = 12.

Is the number 12 a Perfect Square?

The prime factorization of 12 = 2² × 3¹. Here, the prime factor 3 is not in the pair. Therefore, 12 is not a perfect square.

Evaluate 2 plus 15 square root 12

The given expression is 2 + 15 √12. We know that the square root of 12 is 3.464. Therefore, 2 + 15 √12 = 2 + 15 × 3.464 = 2 + 51.962 = 53.962

Math worksheets and
visual curriculum