A day full of math games & activities. Find one near you.

Square Root of 36

The square root of 36 is expressed as √36 in the radical form and as (36)^½ or (36)^0.5 in the exponent form. The square root of 36 is 6. It is the positive solution of the equation x² = 36. The number 36 is a perfect square.

Square Root of 36: 6
Square Root of 36 in exponential form: (36)^½ or (36)^0.5
Square Root of 36 in radical form: √36

1.	What Is the Square Root of 36?
2.	Is Square Root of 36 Rational or Irrational?
3.	How to Find the Square Root of 36?
4.	faqSection

What Is the Square Root of 36?

The square root of a number is a number whose square gives the original number. For example, to find the square root of 36 (which is denoted by √36), we have to think of a number whose square is 36
You can remember it this way: When the square moves from one side to the other side of the equation, it becomes the square root.

6² = 36
√36 = 6

Thus, the square root of 36 is 6.

Is the Square Root of 36 Rational or Irrational?

A rational number can be expressed as a fraction of integers. We already found that

√36 = 6 = 6/1

So we could express √36 as a fraction of integers and hence it is a rational number.

√36 is a rational number.

How to Find the Square Root of 36?

We can find the square root of 36 using various methods.

Repeated Subtraction
Prime Factorization
Estimation and Approximation
Long Division

If you want to learn more about each of these methods, click here.

We know that 36 is a perfect square, so we can find its square root using the prime factorization method easily.

Square Root of 36 Using Prime Factorization

The prime factorization of 36 is as follows:

36 is: 36 = 2 × 2 × 3 × 3

To find the square root of 36, we take one number from each pair of the same numbers and multiply them.

√36 = 2 × 3 = 6

Square Root of 36 By Long Division

The square root of 36 can be found using the long division as follows.

Think of a number which when multiplied by itself gives

a number that is less than or equal to 36
a number that is very close to 36

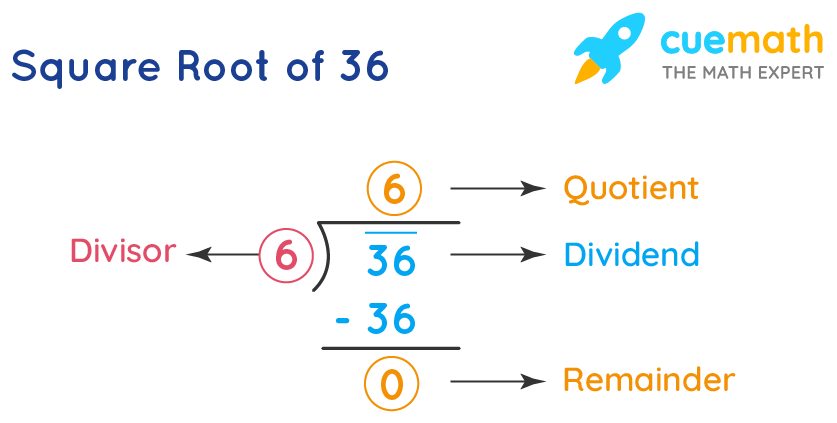
Find the square root of 36 by long division

Since the remainder is 0, we do not need to proceed with long division further and we consider the quotient (which is 6) as the result.

√36 = 6

Explore square roots using illustrations and interactive examples.

Think Tank:

Can the value of √36 be -6 as well?
Hint: Think what is (-6)²
Is √-36 a real number?
Hint: Think whether there is any real number whose square is negative.

Important Notes:

If we do not have pairs of the same numbers as above, then the prime factorization cannot be used to find the exact square root. Instead, we have to use the long division method.
The prime factorization method is used to write a square root of a non-perfect square number in the simplest radical form.
For example:
18 = 2 × 3 × 3 = 2 × 3²
So, √18 = √2 × √3² = 3√2

Square Root of 36 Solved Examples

Example 1

Jack is instructed to find the square root of 36 using the laws of exponents. Can we help him with this?

Solution

The square root can be always replaced with the exponent 1/2.
√36 = 36^½
= (6²)^½

Since 6² = 36 = 6 [(a^m)ⁿ = a^mn]
Thus, √36 = 6
Example 2

There are as many seats in a minivan as the number of rows in it. If there are 36 seats in it, then how many rows are there?

Solution

Let us assume the number of seats in the minivan is y.
By the given information,
y×y = 36
y² = 36
By taking the square root on both sides,
√y² = √36
We know that the square root of y² is y.
Also, we know that 6² = 36 and so the square root of 36 is 6
y= 6

The number of rows = 6
Example: If the area of an equilateral triangle is 36√3 in². Find the length of one of the sides of the triangle.

Solution:

Let 'a' be the length of one of the sides of the equilateral triangle.
⇒ Area of the equilateral triangle = (√3/4)a² = 36√3 in²
⇒ a = ±√144 in
Since length can't be negative,
⇒ a = √144 = 2 √36
We know that the square root of 36 is 6.
⇒ a = 12 in

go to slide go to slide go to slide

Breakdown tough concepts through simple visuals.

Math will no longer be a tough subject, especially when you understand the concepts through visualizations.

Book a Free Trial Class

FAQs on the Square Root of 36

What is the Value of the Square Root of 36?

The square root of 36 is 6.

Why is the Square Root of 36 a Rational Number?

Upon prime factorizing 36 i.e. 2² × 3², we find that all the prime factors are in even power. This implies that the square root of 36 is a positive integer. Therefore, the square root of 36 is rational.

What is the Square Root of -36?

The square root of -36 is an imaginary number. It can be written as √-36 = √-1 × √36 = i √36 = 6i
where i = √-1 and it is called the imaginary unit.

What is the Value of 19 square root 36?

The square root of 36 is 6. Therefore, 19 √36 = 19 × 6 = 114.

Evaluate 10 plus 13 square root 36

The given expression is 10 + 13 √36. We know that the square root of 36 is 6. Therefore, 10 + 13 √36 = 10 + 13 × 6 = 10 + 78 = 88

Is the number 36 a Perfect Square?

The prime factorization of 36 = 2² × 3². Here, all the numbers are in the power of 2. This implies that the square root of 36 is a positive integer. Therefore, 36 is a perfect square.

Math worksheets and
visual curriculum