Square Root of 5

The square root of 5 is expressed as √5 in the radical form and as (5)^½ or (5)^0.5 in the exponent form. The square root of 5 rounded up to 5 decimal places is 2.23607. It is the positive solution of the equation x² = 5.

• Square Root of 5: 2.23606797749979
• Square Root of 5 in exponential form: (5)^½ or (5)^0.5
• Square Root of 5 in radical form: √5

Let us first understand the meaning of square root. The square root of a number is the number which, when multiplied to itself, gives the product as the original number. Consider the example:

• 5² = 5 × 5 is 25

Here 5 is called the square root of 25. 25 is a perfect square. So the square root of 25 is 5. Now, what is the square root of 5? Does that mean non-square numbers cannot have a square root? Non-square numbers also have a square root, just that they are not whole numbers. For real numbers a and b,

• a²=b is a=√b

The square root of 5 in the radical form is expressed as √5 and in exponent form, it is expressed as 5½. The square root of 25 is the inverse operation of squaring 5 and -5

• 5 × 5=25
• (-5) × (-5) = 25. 

Let us look at the square root of 5

Square Root of 5

We know that factors of 5 are 5 × 1 = 5

• √5 = 2.23
• 5 is not a perfect square.

A number that can be expressed as a ratio of two integers, that is, p/q, q ≠ 0 is called a rational number. Now let us look at the square root of 25. √25 = 5 = 5/1. Thus, √25 is a rational number. Now let us look at the square root of 5

• √5 = 2.23

A number that cannot be expressed as a ratio of two integers is called an irrational number.

• 5 is not a perfect square.
• The square root of 5 is an irrational number.

There are different methods to find the square root of 5. The first method is by prime factorization and the second is the conventional long division method.

Square Root of 5 Using Prime Factorization

Let us find the square root of 5 using prime factorization:

• 5 = 5 × 1
• 5 = 5

Taking square root

• √5 = √5
• √5 = 2.23

Let us now try finding the square root of 5 by the long division method.

Square Root of 5 By Long Division

Let us follow these steps to find the square root of 5 by the long division method.

• Step 1: Group the digits into pairs (for digits to the left of the decimal point, pair them from right to left) by placing a bar over them. Since our number is 5, let us represent it inside the division symbol.
• Step 2: Find the largest number such that when you multiply it with itself, the product is less than or equal to 5. We know that  2 × 2 is 4 and is less than 5. Now let us divide 5 by 2
• Step 3: Let us place a decimal point and pairs of zeros and continue our division. Now, multiply the quotient by 2 and the product becomes the starting digit of our next divisor.
• Step 4: Choose a number in the unit's place for the new divisor such that its product with a number is less than or equal to 100. We know that 2 is in the ten's place and our product has to be 100 and the closest multiplication is 42 × 2 = 84
• Step 5:  Bring down the next pair of zeros and multiply the quotient 22 (ignore the decimal) by 2, which is 44 and the starting digit of the new divisor.
• Step 6: Choose the largest digit in the unit's place for the new divisor such that the product of the new divisor with the digit at one's place is less than or equal to 1600. We see that 443, when multiplied by 3, gives 1329 which is less than 1600. Our long division now looks like

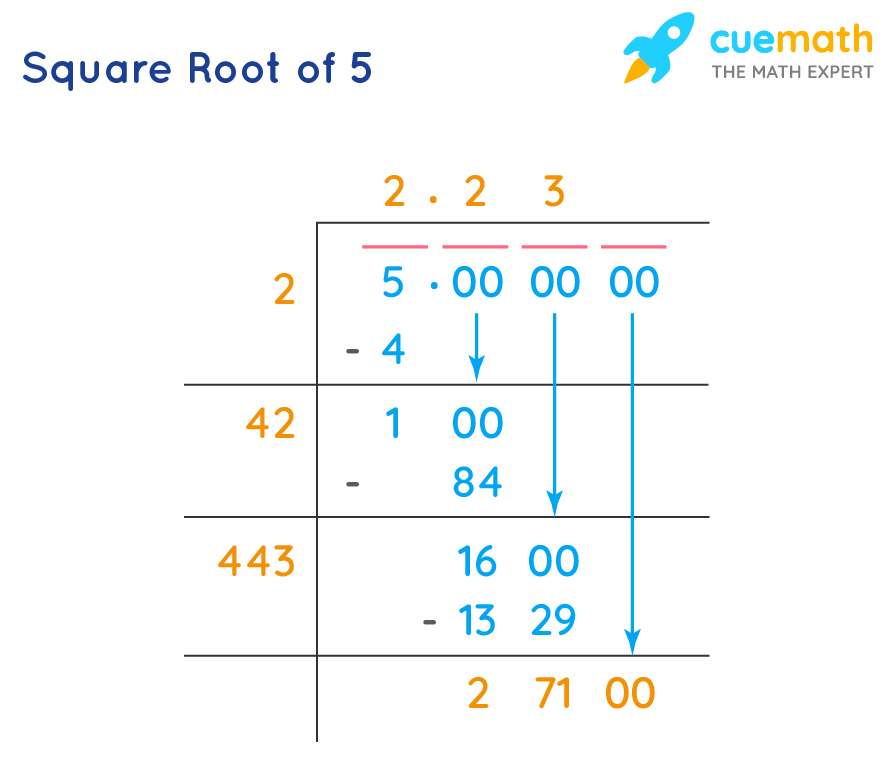
• Step 7: Add more pairs of zeros and repeat the process of finding the new divisor and product as in step 2

Note that the square root of 5 is an irrational number, i.e, it is never-ending. So, stop the process after 4 or 5 iterations, and you have the square root of 5 by the long division method.

Explore Square roots using illustrations and interactive examples

• Square Root of 25
• Square Root of 35
• Square Root of 65
• Square Root of 85
• Square Root of 15

• Evaluate the following:

  a) 5√25 + 5√4 + 5√16
  b) 5√5 + 7√5 - 10√5
  c) 5√6 + 5√25 - 5

• The square root of 5 in the radical form is expressed as √5.
• In exponent form, the square root of 5 is expressed as 5^½.