A day full of math games & activities. Find one near you.

Square Root of 85

The square root of 85 is expressed as √85 in the radical form and as (85)^½ or (85)^0.5 in the exponent form. The square root of 85 rounded up to 10 decimal places is 9.2195444573. It is the positive solution of the equation x² = 85.

Square Root of 85: 9.219544457292887
Square Root of 85 in exponential form: (85)^½ or (85)^0.5
Square Root of 85 in radical form: √85

1.	What Is the Square Root of 85?
2.	Is Square Root of 85 Rational or Irrational?
3.	How to Find the Square Root of 85?
4.	Challenging Questions
5.	FAQs on Square Root of 85

What Is the Square Root of 85?

The square root of a number is the number which, when multiplied to itself, gives the original number. The square root of 85 is 9.21 and is shown as √85 = 9.21. The value of the square root of 85 lies between the whole numbers 9 and 10.

Is the Square Root of 85 Rational or Irrational?

The square root of 85 is a non-terminating decimal, i.e., √85 = 9.219544. Also, it cannot be expressed in the form of a fraction p/q, and hence, it is an irrational number.

How to Find the Square Root of 85?

The number 85 is not a perfect square, so its value can be approximated between 9 and 10. √85 = 9.21. The exact value of the square root of 85 can be calculated using long division. This method to find the square root of 85 is similar to the normal division, where the quotient represents the square root value. Further, since 85 is not a perfect square, the remainder is never 0 and the division process is concluded after a few steps.

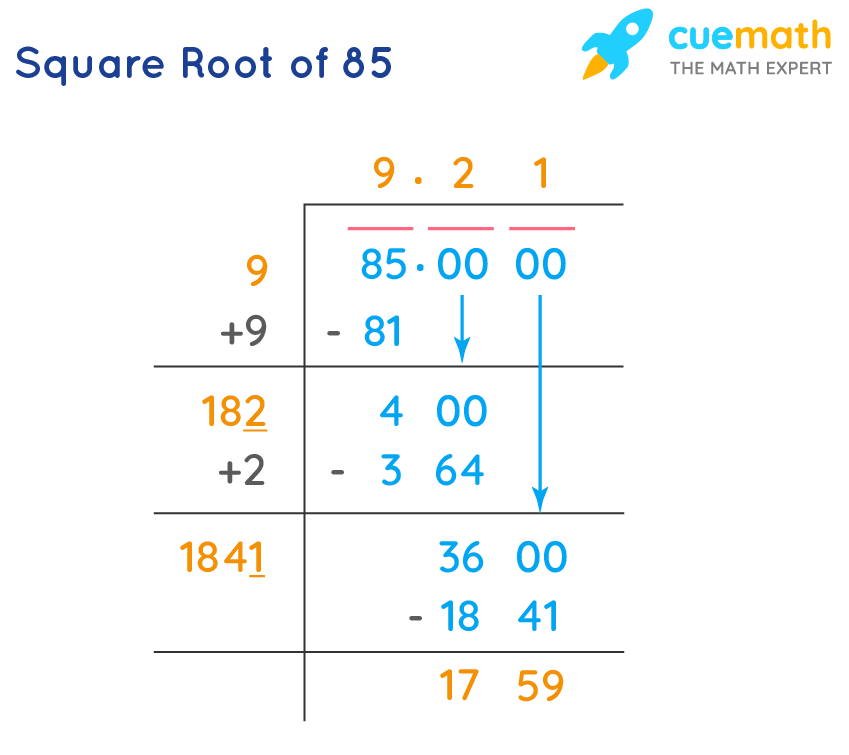
Square Root of 85 By Long Division

The square root of 85 can be found by the following long division method. Let's see the steps to find the square root of 85 by the long division method.

Step 1: Divide the number 85 by 9, because 9² = 81 is a perfect square number that is less than 85.
Step 2: The divisor and the quotient need to be the same numbers; in this case, it is 9. Multiply the quotient and the divisor and subtract the result 81 from 85.
Step 3: For the next divisor, add the previous divisor with the quotient. (9 + 9 = 18); place it as the new divisor with a blank on its right.
Step 4: Put a decimal after quotient 9 and bring down two zeros to place it after 4 so that it becomes 400. The blank needs to be filled with a number, such that when the new divisor is multiplied with the new quotient, the product is less than or equal to the dividend. [182 × 2 = 364] Subtract 364 from 400 [400 - 364 = 36].
Step 5: Bring down two zeros again and place it after 36, so that it becomes 3600. Take the new quotient 2 and add it to 182 [182 + 2 = 184]. Repeating the above steps, we need to fill the blank with a number such that when the new divisor is multiplied with the new quotient, the product is less than or equal to the dividend 3600.
Step 6: Repeat the process till we get the remainder equal to zero. This is how the square root of 85 up to two places is obtained by the long division method.

Long division for square root of 85

Explore square roots using illustrations and interactive examples

Challenging Questions:

Find the square root of √8585
Simplify (((√85)^½)^¾)

Square Root of 85 Solved Examples

Example 1: Jack needs to cut a square-shaped cardboard for his school assignment. The required area of the cardboard is 85 square inches. Can you help Jack find the length of each side of the cardboard?

Solution

Given that the area of the cardboard is 85 square inches.
Area of the square = x²
Let's calculate the value of x.
x² = 85
x = √85
x = 9.2
Thus, the length of each side of the cardboard is 9.2 inches.
Example 2

A cultural club was formed and the members decided to collect an annual subscription fee. The annual subscription fee equals the total number of members in the club. If the total subscription fee collected is $7225, find the number of members in the club.

Solution:

Given that the number of members in the club is equal to the value of the subscription amount per member.
Let the number of members in the club = Subscription per member = x
Total subscription received = $7225
Number of members X subscription per member = $7225
x × x = 7225
x² = 7225
x = √7225
x = √(85 × 85)
x = 85
Thus, the subscription per member is $85.
Example: If the area of an equilateral triangle is 85√3 in². Find the length of one of the sides of the triangle.

Solution:

Let 'a' be the length of one of the sides of the equilateral triangle.
⇒ Area of the equilateral triangle = (√3/4)a² = 85√3 in²
⇒ a = ±√340 in
Since length can't be negative,
⇒ a = √340 = 2 √85
We know that the square root of 85 is 9.220.
⇒ a = 18.439 in

go to slide go to slide go to slide

Ready to see the world through math’s eyes?

Math is a life skill. Help your child perfect it through real-world application.

Book a Free Trial Class

FAQs on the Square Root of 85

What is the Value of the Square Root of 85?

The square root of 85 is 9.21954.

Why is the Square Root of 85 an Irrational Number?

Upon prime factorizing 85 i.e. 5¹ × 17¹, 5 is in odd power. Therefore, the square root of 85 is irrational.

If the Square Root of 85 is 9.220. Find the Value of the Square Root of 0.85.

Let us represent √0.85 in p/q form i.e. √(85/100) = 0.85/10 = 0.922. Hence, the value of √0.85 = 0.922

What is the Square of the Square Root of 85?

The square of the square root of 85 is the number 85 itself i.e. (√85)² = (85)^2/2 = 85.

What is the Square Root of 85 in Simplest Radical Form?

We need to express 85 as the product of its prime factors i.e. 85 = 5 × 17. Therefore, as visible, the radical form of the square root of 85 cannot be simplified further. Therefore, the simplest radical form of the square root of 85 can be written as √85

Is the number 85 a Perfect Square?

The prime factorization of 85 = 5¹ × 17¹. Here, the prime factor 5 is not in the pair. Therefore, 85 is not a perfect square.

Math worksheets and
visual curriculum