Square Root of 18

The square root of 18 is the number when multiplied with itself results in 18. The square root of a number is both positive and negative of the numerical value we obtain using different methods. In this mini-lesson, we will calculate the square root of 18 by prime factorization and long division method along with few interesting problems.

• Square root of 18: √18 = 4.2426
• Square of 18: 18² = 324

• The square root of a number is the number when multiplied by itself results in the original number.
• The square root of 18 is written as √18 = 4.2426
• Square root of 18 in radical form = √18 = √(2 × 3 × 3) = 3√2
• Hence, 18 is not a perfect square

• A rational number is defined as a number that can be expressed in the form of p/q where q ≠ 0
• The square root of 18 is a non-repeating and non-terminating number. Hence, the square root of 18 cannot be represented as a ratio of two integers.
• Therefore, the square root of 18 is an irrational number.

The square of 18 can be evaluated using the prime factorization method or long division method.

Square Root of 18 by Prime Factorization Method

To find the square root of 18 firstly we will find the prime factorization of 18
18 = 2 × 3 × 3
18 = 2 × 3²
Now this can be simplified into √18 = √(2 × 3²)
√18 = √2 × √3²
√18 = 3√2
Therefore, the square root of 18 can be simplified as √18 = 3√2

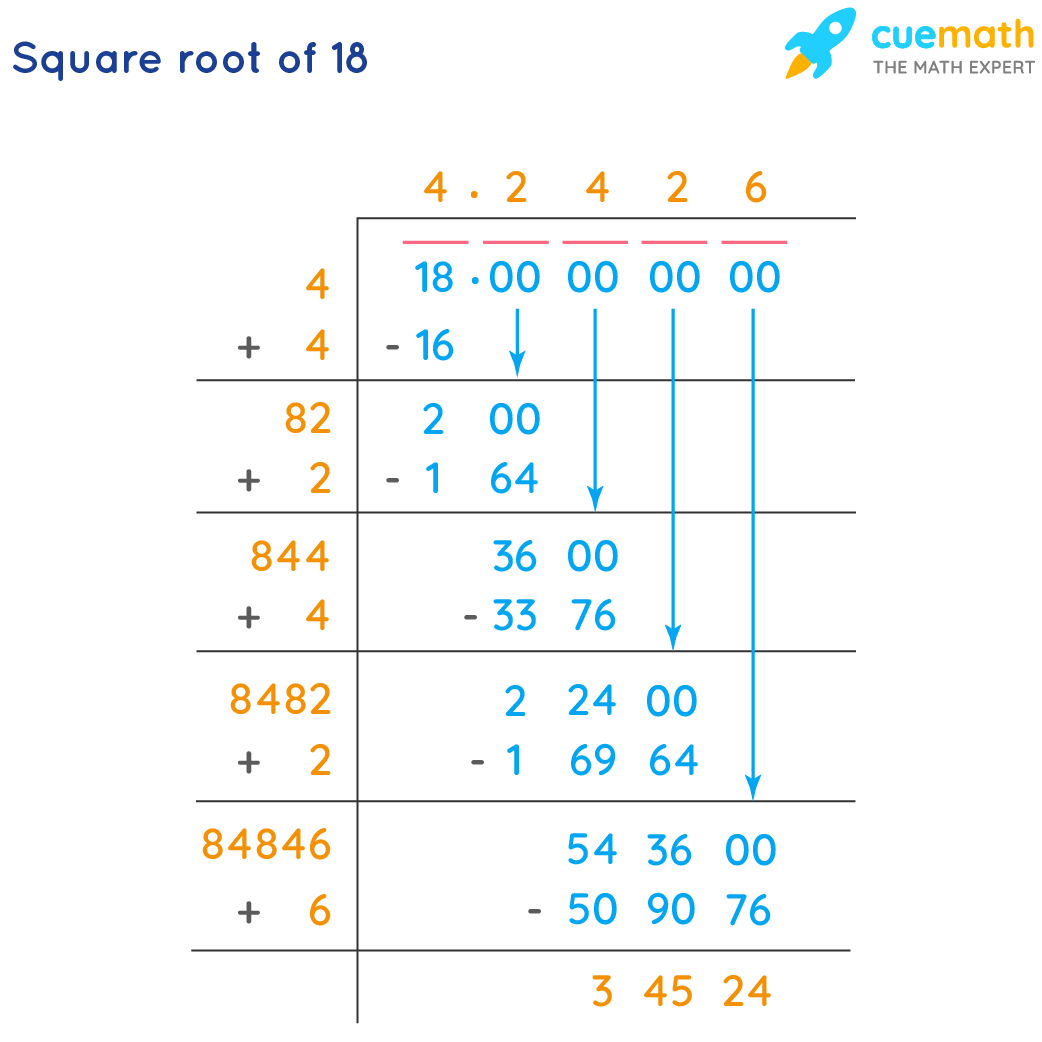
Square Root of 18 By Long Division

With the help of the following steps, we can find the square root of 18 via the long division method.

• Write 18 as shown in the diagram. Start grouping the digits from the right end by putting a bar on top of them.
• Now find a number which when multiplied with itself gives a number less than equal to 18. We know that 4 × 4 = 16
• Calculate the difference as done in the usual division and add the divisor with itself that was calculated in the previous part. The divisor will become 8 and the remainder will be 2.
• Now we have no more number in the dividend left so, we put a decimal point after the dividend and quotient. Then place four pairs of zeros after the decimal of the dividend and bring the pair of zeros down.
• Find a number for the unit’s place of divisor such that will result in a number less than equal to 200.
• Bring the next pair of zeros down and repeat the steps till the last pair of zeros.
• Therefore, we get the square root of √18 = 4.2426 by the long division method.

Explore square roots using illustrations and interactive examples

• Square root of 98
• Square root of 29
• Square root of 11
• Square root of 17
• Square root of 19

• There will be n/2 digits in the square root of an even number with n digits.
• There will be (n+2)/2 digits in the square root of an odd number with n digits
• The square root of 18 is represented as √18 in radical form.
• The square root of 18 is represented as (18)^1/2 in exponential form.

• Find the value of √√18?
• Jake initially planned to make a square-shaped pool of area 20 square feet but was only able to make a pool with an area of 18 square feet. By how many feet the side of the pool is short than what was initially planned?

What is the square root of -18?

The square root of negative numbers is imaginary.
It is expressed as √-18 = 3√2 i.

Can we find the square root of 18 by the repeated subtraction method?

No, we can’t calculate the square root of 18 by repeated subtraction method
This method can only be used if the given number is a perfect square but 18 is not a perfect square.

What is the prime factorization of 18?

Prime factorization of 18: 2 × 3²

Is the square root of 18 is a rational number?

No, the square root of 18 is not a rational number
Because the square root of 18 is a non-repeating and non-terminating number. Hence, cannot be represented in the p/q form.

Is -3√2 is the square root of 18?

Yes, -3√2 is a square root of 18 along with 3√2
As -3√2 × -3√2 = 18