A day full of math games & activities. Find one near you.

Square Root of 8

The square root of 8 is expressed as √8 in the radical form and as (8)^½ or (8)^0.5 in the exponent form. The square root of 8 rounded up to 8 decimal places is 2.82842712. It is the positive solution of the equation x² = 8. We can express the square root of 8 in its lowest radical form as 2 √2.

Square Root of 8: 2.8284271247461903
Square Root of 8 in exponential form: (8)^½ or (8)^0.5
Square Root of 8 in radical form: √8 or 2 √2

1.	What Is the Square Root of 8?
2.	Is Square Root of 8 Rational or Irrational?
3.	How to Find the Square Root of 8?
4.	Important Notes on Square Root of 8
5.	Thinking Out of the Box!
6.	FAQs on Square Root of 8

What Is the Square Root of 8?

We know that addition has an inverse operation as subtraction and multiplication has an inverse operation as division. Similarly, finding the square root is an inverse operation of squaring a number. The square root of 8 gives a number that when multiplied to itself gives the number 8. Hence, we have to think of a number whose square is 8.

Is the Square Root of 8 Rational or Irrational?

A rational number is a number that can be expressed in the form of p/q, where p and q are integers and q is not equal to 0. A number that is not a rational number is called an irrational number. Non-terminating decimals that have repeated numbers after the decimal point are rational numbers. Now let us look at the square root of 8. The decimal representation of √8 is 2.828427125

Do you think the decimal part stops after 2.828427125?

No, it is never-ending. It is a non-terminating decimal with non-repeating digits. The number 2.828427125... can't be written in p/q form.

Hence, the square root of 8 is not a rational number. It is an irrational number.

How to Find the Square Root of 8?

We will discuss two methods to find the square root of 8.

Simplifying the radical of the numbers that are perfect squares
Long division method for perfect and non-perfect squares

The prime factorization of 8 is 8 = 2 × 2 × 2. Therefore, √8 can be simplified further as √8 =√(2 × 2 × 2) = 2√2. Thus, we have expressed the square root of 8 in the simplest radical form as 2√2

So, √8 = 2√2

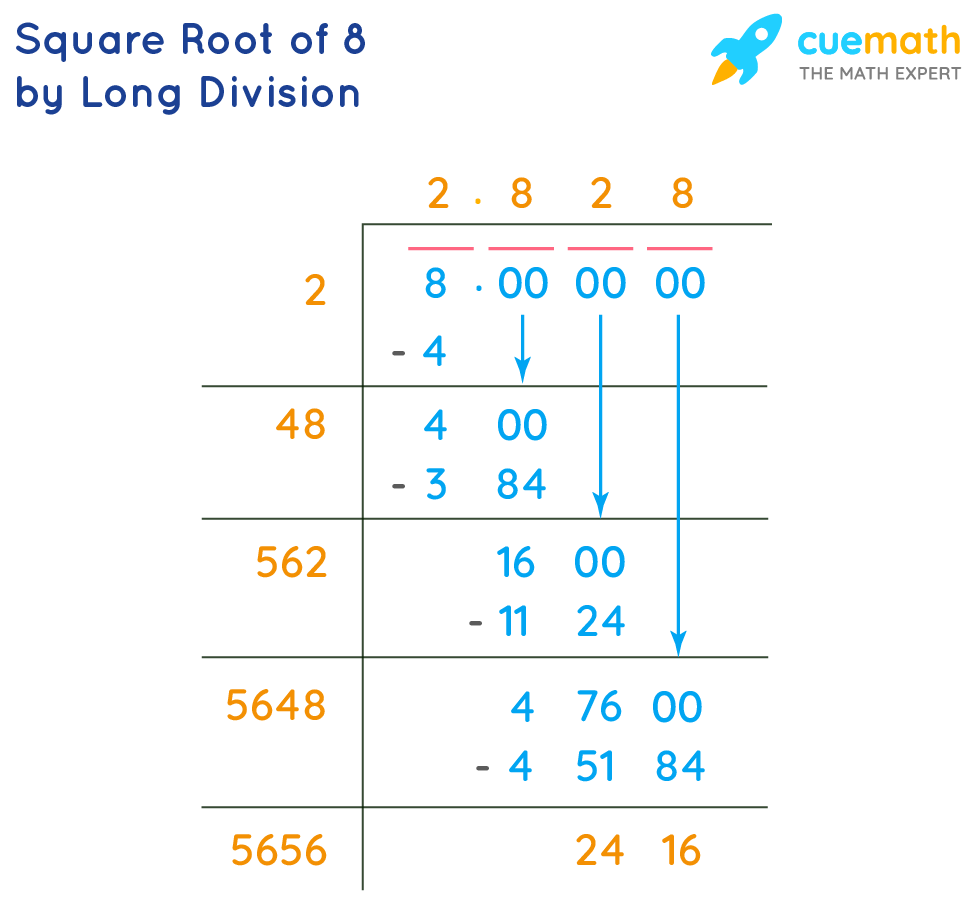
Square Root of 8 by Long Division Method

The value of the square root of 8 by long division method consists of the following steps:

Step 1: Starting from the right, we will pair up the digits by putting a bar above them.
Step 2: Find a number that, when multiplied to itself, gives the product less than or equal to 8. So, the number is 2. Keeping the divisor as 2, we get the quotient as 2 and the remainder as 4.
Step 3: Double the divisor and enter it with a blank on its right. Guess the largest possible digit to fill in the blank which will become the new digit in the quotient, such that when the new divisor is multiplied to the new quotient the resultant product is less than or equal to the dividend. Divide and write the remainder. Repeat this process to get the decimal places you want.

Can you use this method to find the square root of 7?

Explore square roots using illustrations and interactive examples

Important Notes:

Square root is the inverse operation of squaring.
Square root of 8 can be expressed as √8 = 8^1/2.
We can find the square root of 8 using the radical form and the long division method.

Think Tank:

We know that (-2√2) × (-2√2) = 8. So, can we say that -2√2 is a square root of 8?
Can you determine a quadratic equation whose roots are 2√2 and -2√2?

Example 1: Mr. Smith wants to fence his square garden. The garden has an area of 8 square feet. How long is each side of the garden?

Solution

To find the side of the square garden, we will have to find the square root of 8. The square root of 8 is √8 = 2√2. Hence, the side length of the garden is 2√2 feet.

Example 2: Lucy is doing yoga in her yard. The gate in her yard has an area of 12 square feet. What is the height of the gate?
Example 2: Lucy is doing yoga in her yard. The gate in her yard has an area of 12 square feet. What is the height of the gate?

Solution

By finding the square root of the area of the gate, we can find the side length of the gate.

Using the property of square roots, we have √12 = √3 × √4 = √3 × 2 = 2√3

Hence, the side length of the gate is 2√3 feet.
Example 3: If the area of a square is 8 in². Find the length of the side of the square.

Solution:

Let 'a' be the length of the side of the square.
⇒ Area of the square = a² = 8 in²
⇒ a = ±√8 in
Since length can't be negative,
⇒ a = √8 = 2.828 in

go to slide go to slide go to slide

Have questions on basic mathematical concepts?

Become a problem-solving champ using logic, not rules. Learn the why behind math with our certified experts

Book a Free Trial Class

FAQs on the Square Root of 8

What is the Value of the Square Root of 8?

The square root of 8 is 2.82842.

Why is the Square Root of 8 an Irrational Number?

Upon prime factorizing 8 i.e. 2³, 2 is in odd power. Therefore, the square root of 8 is irrational.

What is the Square Root of 8 in Simplest Radical Form?

We need to express 8 as the product of its prime factors i.e. 8 = 2 × 2 × 2. Therefore, √8 = √2 × 2 × 2 = 2 √2. Thus, the square root of 8 in the lowest radical form is 2 √2.

If the Square Root of 8 is 2.828. Find the Value of the Square Root of 0.08.

Let us represent √0.08 in p/q form i.e. √(8/100) = 0.08/10 = 0.283. Hence, the value of √0.08 = 0.283

What is the Square Root of -8?

The square root of -8 is an imaginary number. It can be written as √-8 = √-1 × √8 = i √8 = 2.828i
where i = √-1 and it is called the imaginary unit.

Is the number 8 a Perfect Square?

The prime factorization of 8 = 2³. Here, the prime factor 2 is not in the pair. Therefore, 8 is not a perfect square.

Math worksheets and
visual curriculum