A day full of math games & activities. Find one near you.

Perimeter of Isosceles Triangle

The perimeter of an isosceles triangle is the total length of its boundary which means the sum of all its sides. A triangle is considered to be an isosceles triangle if it has two equal sides and two equal angles. Let us learn more about the perimeter of an isosceles triangle using solved examples.

1.	Perimeter of Isosceles Triangle
2.	Perimeter of Isosceles Triangle Formula
3.	Perimeter of Isosceles Right Triangle
4.	FAQs on Perimeter of Isosceles Triangle

Perimeter of Isosceles Triangle

The perimeter of an isosceles triangle is the sum of all the three sides. Since an isosceles triangle has 2 equal sides, the perimeter is twice the equal side plus the different side. It is measured in linear units such as inches (in), yards (yd), millimeters (mm), centimeters (cm), and meters (m). Let us understand the formula to find the perimeter in the next section.

Perimeter of Isosceles Triangle Formula

The perimeter of an isosceles triangle is calculated by adding the length of all its three sides. Since an isosceles triangle has two equal sides, its perimeter can be calculated if the base and one equal side is known. The formula used to find the perimeter of an isosceles triangle is: Perimeter of isosceles triangle (P) = 2a + b

where, a = the length of the equal sides; b = the length of the base (unequal side)

Derivation of the formula: Observe the figure given below which will help us to derive the formula for the perimeter of an isosceles triangle. Let us consider an isosceles triangle ABC in which side AB = AC. Now, if the equal sides are named as 'a' and the unequal side is named as 'b', the sum of all its sides will be: AB + AC + BC, or, a + a + b. Therefore, the perimeter of an isosceles triangle is : 2a + b

Perimeter of an Isosceles Triangle Formula

Perimeter of Isosceles Right Triangle

The perimeter of an isosceles right-angled triangle can be found by adding the length of all its three sides. Since it is a right-angled triangle, one of its sides is the hypotenuse and the other two sides are equal. If the length of the hypotenuse is 'h' units and the lengths of the other two sides are 'l', then the perimeter of an isosceles right triangle would be: Perimeter of isosceles right triangle = h + l + l. Observe the following figure to understand the dimensions and the formula of an isosceles right triangle.

Perimeter of an Isosceles Right Triangle

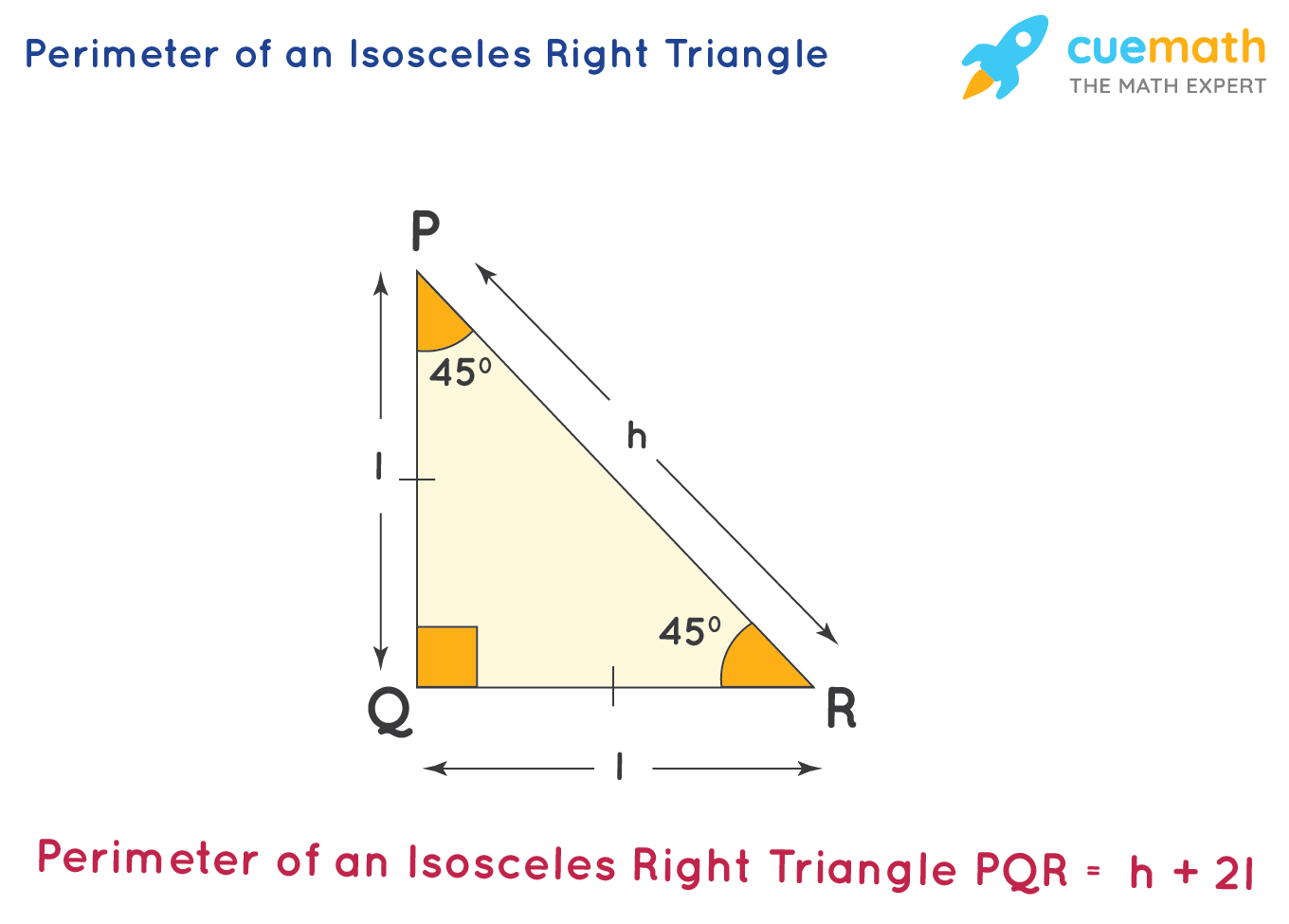
As given in the figure, the perimeter of an isosceles right triangle is P = h + 2l.

Now, let us find the perimeter of an isosceles right triangle in 2 different scenarios given below. If we apply the Pythagoras theorem in the figure, we get h = √(l²+ l²) = √2 × l. This means h = √2 × l, which can also be written as: l = h/√2. These values can be substituted with each other if one of them is not known.

When the length of the equal side is given: Referring to the explanation given above, if the length (l) is given, then the perimeter of an isosceles right triangle will be (P) = 2l + (√2)l = (2 + √2)l
When the hypotenuse is given: Referring to the explanation given above, if the hypotenuse (h) is given, then the perimeter of an isosceles right triangle will be (P) = h + 2(h/√2) = h + √2h = h(1 + √2)

It should be noted that the two congruent angles in the isosceles right triangle measure 45° each.

Important Notes on Perimeter of Isosceles Triangle

Here is a list of a few points that should be remembered while studying the perimeter of an isosceles triangle:

A triangle is considered to be an isosceles triangle if it has two equal sides.
Since an isosceles triangle has two equal sides, its perimeter can be calculated if the base and the equal sides are known.
The formula to calculate the perimeter of an isosceles triangle is P = 2a + b where 'a' is the length of the two equal sides and 'b' is the base of the triangle.
The perimeter of an isosceles right triangle can be calculated with the help of the formula: P = h + 2l, where 'h' is the length of the hypotenuse and 'l' is the length of the adjacent sides.

☛ Related Topics

Examples on Perimeter of Isosceles Triangle

Example 1: What is the perimeter of an isosceles triangle when the length of one of the equal sides = 10 cm and the base = 6 cm?

Solution:

To find the perimeter of isosceles triangle, we use the formula: perimeter = 2a + b. In this case, the length of one equal side (a) = 10 cm; base (b) = 6 cm

Substituting the values in the formula:
= 2 (10) + 6
= 20 + 6
= 26 cm

Answer: The perimeter of the given isosceles triangle is 26 cm.
Example 2: The perimeter of an isosceles triangle is 12 units. Find out the length of the third side of the triangle if the equal sides measure 3 units each.

Solution: Let the third side of the isosceles triangle be 'b'

Given, Perimeter = 12 units, a = 3 units, b = ?

Using the formula for the perimeter of isosceles triangle = 2a + b

Substituting the given values in the above formula,

12 = 2 (3) + b
12 = 6 + b

12 - 6 = b

Therefore, b = 6 units

Answer: The third side of the triangle measures 6 units.
Example 3: Find the perimeter of an isosceles right triangle in which the hypotenuse is 8 units.

Solution: When only the hypotenuse is given, the perimeter of an isosceles right triangle can be calculated with the formula, Perimeter of isosceles right triangle = h(1 + √2); where h = hypotenuse

After substituting the value of h = 8, we get, Perimeter of isosceles right triangle = h(1 + √2) = 8(1 + √2) units.

go to slide go to slide go to slide

Have questions on basic mathematical concepts?

Become a problem-solving champ using logic, not rules. Learn the why behind math with our Cuemath’s certified experts.

Book a Free Trial Class

Practice Questions on the Perimeter of Isosceles Triangle

go to slide go to slide

FAQs on the Perimeter of Isosceles Triangle

What is the Perimeter of Isosceles Triangle?

The perimeter of an isosceles triangle is the sum of all the three sides. Since an isosceles triangle has two equal sides, the perimeter is twice the equal side plus the different side.

How to find the Perimeter of an Isosceles Triangle?

The perimeter of an isosceles triangle is the total length of its boundary. Since an isosceles triangle has 2 equal sides and one different side, the formula that is used to find the perimeter is, Perimeter of isosceles triangle = 2a + b; where 'a' is one of the equal sides and 'b' is the unequal side. The perimeter is measured in linear units like centimeters, meters, inches, and so on.

What is the Formula for the Perimeter of an Isosceles Triangle?

The formula that is used to calculate the perimeter of an isosceles triangle is, Perimeter = 2a + b, where 'a' represents the length of one of the equal sides and 'b' is the base or the 3rd side.

What is the Formula of the Perimeter of an Isosceles Right Triangle?

The perimeter of an isosceles right triangle is calculated with the help of the formula: P = h + 2l, where 'h' is the length of the hypotenuse and 'l' is the length of the adjacent sides. Since it is a right-angled triangle, we can apply the Pythagoras theorem and calculate the perimeter using only the length or the hypotenuse, whichever is given. The formula using only the length is: P = (2 + √2)l. Similarly, the formula using only the hypotenuse is: P = h(1 + √2).

What is the Formula to Calculate the Perimeter of a Triangle?

The perimeter of a triangle can be found by calculating the sum of all its sides. So, the formula for calculating the perimeter of a triangle with side lengths a, b, and c, would be: Perimeter = a + b + c.

What is the Area and Perimeter of Isosceles Triangle?

The area of an isosceles triangle is the region covered by it. This is calculated with the help of the formula, Area = 1/2 × base × height. On the other hand, the perimeter of isosceles triangle is the total length of its boundary. This is calculated with the help of the formula, perimeter of isosceles triangle = 2(a + b); where 'a' = length of one of the equal sides; b = the length of the base (unequal side).

How to Find the Perimeter of an Isosceles Triangle if the Area is Given?

The perimeter of an isosceles triangle can be calculated if the area and height are known. Let us understand this with an example using the following steps. If the area of an isosceles triangle is 90 square units, and the height of the triangle is 9 units, let us find the perimeter.

Step 1: Using the area, A = 90 units², and height, h = 9 units, we can calculate the base (b) of the isosceles triangle using the formula, Base = (2 × Area)/height. In this case, base = (2 × 90)/9 = 20 units.
Step 2: We know that the height of an isosceles triangle bisects the base, so, we can divide the base by 2 to get the dimension of the right triangle that is formed once the height of the triangle is drawn. So, the base which is equal to 20 units can be divided by 2 to get 10.
Step 3: Now, we know two sides of the right-angled triangle, and we need to find the hypotenuse. We can use the Pythagoras theorem to find the hypotenuse with the help of this bisected base (10 units) and height (9 units). The hypotenuse will be, Hypotenuse² = base² + height² = 10² + 9² = 100 + 81 = 181. Therefore, hypotenuse = √181 = 13.45 units
Step 4: This hypotenuse is one of the equal sides of the isosceles triangle. So, now we can easily find the perimeter of the isosceles triangle which is, P = 2a + b. Perimeter = (2 × 13.45) + 20 = 46.9 units.

How to Find the Perimeter of an Isosceles Triangle on a Coordinate Plane?

If the coordinates of the vertices of an isosceles triangle are given, we can calculate the perimeter by finding the length of all sides and then further adding them. To calculate the lengths using coordinates, we apply the distance formula and finally find their sum.

How to Find the Perimeter of an Isosceles Triangle with Hypotenuse?

The perimeter of an isosceles triangle can be calculated if only the hypotenuse is given. Since it is an isosceles right-angled triangle, we can apply the Pythagoras theorem and derive a formula which helps to find the perimeter of the triangle with only the hypotenuse given. The formula is expressed as, Perimeter of Isosceles right-angled triangle = h(1 + √2); where 'h' is the hypotenuse. The value of the hypotenuse can be substituted and the perimeter can be calculated.

Download FREE Study Materials

Worksheet on Perimeter

Math worksheets and
visual curriculum