Heights and Distances
In this topic, we will be studying some ways in which trigonometry is used in life around you.
What is meant by trigonometry?
Trigonometry is one of the most ancient subjects studied by scholars all over the world. Trigonometry was invented because its need arose in astronomy. Since then astronomers have used it, for instance, to calculate distances from the Earth to the planets and stars. Trigonometry is also used in geography and in navigation.

The knowledge of trigonometry is used to find heights of structures, construct maps, determine the position of an island in relation to the longitudes and latitudes.
Lesson Plan
What Do You Mean by Height and Distances?
The most significant definitions that are used when dealing with heights and distances are given as:
Line of sight: It is the line drawn from the eye of an observer to the point in the object viewed by the observer.
Here, the cat is the observer and the object is the bird.

The angle of elevation: The angle between the horizontal and the line of sight joining an observation point to an elevated object.
In the following figure, the angle of elevation of the kite from the point \(A\) is \({30^\circ }\), and from point \(B\) is \({60^\circ }\)

The angle of depression: The angle between the horizontal and the line of sight joining an observation point to an object below the horizontal level.
In the following figure, if the top of the building is our observation point, then the angle of depression of person \(X\) is \({45^\circ}\), and that of person \(Y\) is \({60^\circ }\).

Let us now experience how trigonometry is applied to practical situations.
What Are the Formulas for Heights and Distances?
Trigonometric ratios can be used to find heights and distances. Some useful relations are illustrated by the below-given diagrams which help us to determine heights and distances.



-
The angles of depression of the top and the bottom of an \(8\, yd\) tall building from the top of a multi-storeyed building are \(30^\circ \) and \(45^\circ \), respectively. Find the height of the multi-storeyed building and the distance between the two buildings.
Hint: Try to depict the figure according to a given situation.
How to Find Height and Distances?
To measure the heights and distances of different objects, we use trigonometric ratios.

Use the Tangent rule to calculate the height of the tree (above eye level).
tan(angle) = opposite/adjacent
Where the opposite is the height of the tree and adjacent is the distance between you and the tree.
This is rearranged to:
opposite = tan(angle) x adjacent
or more simply
\[\text{height} = \text{tan(angle)} \times \text{distance}\]
Distance can be calculated as:

\(\text{B (distance)} = \dfrac {\text{A (height)}} {\text{tan (e)}}\)
Therefore, to calculate \(B\) (distance) we will need the value of \(A\) (height) and angle \(e\).

1. The angle between the horizontal and the line of sight joining an observation point to an object below the horizontal level is called the angle of elevation.
2. The angle between the horizontal and the line of sight joining an observation point to an object below the horizontal level is called the angle of depression.
3. \(\text{B (distance)} = \dfrac {\text{A (height)}} {\text{tan (e)}}\)

Trigonometric Ratios Table
Values of trigonometric functions for the standard angles such as 0°, 30°, 45°, 60°, and 90° could be easily found using a trigonometric ratios table.
The table consists of trigonometric ratios – sine, cosine, tangent, cosecant, secant, and cotangent.
In short, these ratios are written as sin, cos, tan, cosec, sec, and cot.
It is best to remember the values of the trigonometric ratios of these standard angles.
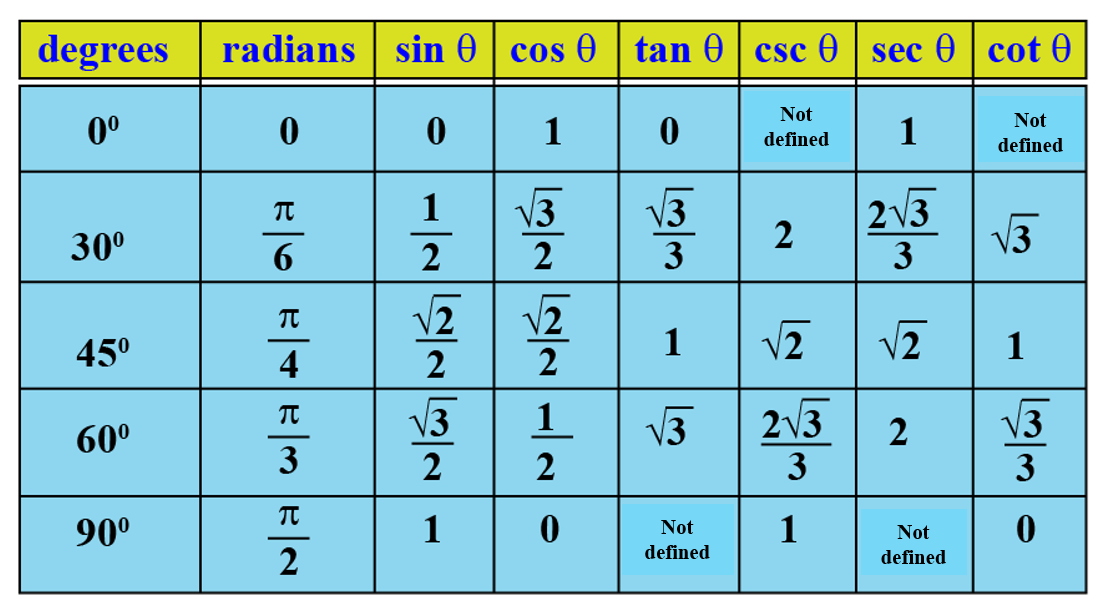
A trigonometric table has wide application in fields like science and engineering.
Solved Examples
| Example 1 |
A man standing at a certain distance from a building, observe the angle of elevation of its top to be \({60^\circ }\). He walks 30 yds away from the building. Now, the angle of elevation of the building’s top is \({30^\circ}\). How high is the building?
Solution
Let the height of the building be \(h\), and \(d\) be the original distance between the man and the building. The following figure depicts the given situation:

We have:
\[\begin{align}
\tan {60^\circ } &= \sqrt 3 \hfill \\
\Rightarrow \frac{h}{d} &= \sqrt 3 \hfill \\
\Rightarrow d &= \frac{h}{{\sqrt 3 }} \hfill \\
\end{align} \]
Also,
\[\begin{align}
\tan {30^\circ } &= \frac{1}{{\sqrt 3 }} \hfill \\
\Rightarrow \frac{h}{{d + 30}} &= \frac{1}{{\sqrt 3 }} \hfill \\
\Rightarrow \sqrt 3 h &= d + 30 \hfill \\
\Rightarrow \sqrt 3 h &= \frac{h}{{\sqrt 3 }} + 30 \hfill \\
\Rightarrow h\left( {\sqrt 3 - \frac{1}{{\sqrt 3 }}} \right) &= 30 \hfill \\
\end{align} \]
\[ \Rightarrow h = 15\sqrt 3 yd \approx 26\;yd\]
|
\(\therefore\) The building's height is about 26 yards. |
| Example 2 |
From a certain point on the ground, the angle of elevation of the top of a tree is \(\alpha \). On moving \(p\) meters towards the tree, the angle of elevation becomes \(\beta \) . Show that the height of the tower is
\[h = \left( {\frac{{p\tan \alpha \tan \beta }}{{\tan \beta - \tan \alpha }}} \right)\;metres\]
Solution
Observe the following figure, which depicts this situation:
Here, \(d\) and \(h\) are unknown and we need to find \(h\) .We have :
\[\tan \beta = \frac{h}{d} \Rightarrow d = h\cot \beta \]
Now, we have,
\[\begin{align}
\tan \alpha &= \frac{h}{{p + d}} \hfill \\
\Rightarrow h &= (p + d)\tan \alpha \hfill \\
&= (p + h\cot \beta )\tan \alpha \hfill \\
&= p\tan \alpha + h\tan \alpha \cot \beta \hfill \\
\Rightarrow h\left( {1 - \tan \alpha \cot \beta } \right) &= p\tan \alpha \hfill \\
\Rightarrow h &= \frac{{p\tan \alpha }}{{1 - \tan \alpha \cot \beta }} \hfill \\
&= \frac{{p\tan \alpha }}{{1 - \frac{{\tan \alpha }}{{\tan \beta }}}} \hfill \\
\end{align} \]
\[ h = \dfrac{p\tan \alpha \tan \beta }{\tan \beta - \tan \alpha }\]
|
\(\therefore\) \( h = \dfrac{p\tan \alpha \tan \beta }{\tan \beta - \tan \alpha }\) |
| Example 3 |
A house has a window \(h\) yards above the ground. Across the street from this house, there is a tall pole. The angle of elevation and depression of the top and bottom of this pole from the window are \(\theta \) and \(\varphi \) respectively. Determine the height of the pole.
Solution
The following figure depicts the given situation:

Note that \(d = h\cot \varphi \) and
\[{h_1} = d\tan \theta = h\tan \theta \cot \varphi \]
Thus, the height of the pole is,
\[\begin{gathered}
H = h + {h_1} \hfill \\
\Rightarrow H = h(1 + \tan \theta \cot \varphi ) \hfill \\
\end{gathered} \]
|
\(\therefore\) The height of the pole is \(= h(1 + \tan \theta \cot \varphi ) \) |
| Example 4 |
From an observation tower, the angle of depression of two cars on the opposite side of the tower are \(\alpha \)and \(\beta \). If the tower’s height is \(h\) yards, find the distance between the cars.
Solution
Observe the following figure:

We have,
\[d_1 = h\cot \alpha, \quad d_2 =h\cot \beta\]
Thus, the distance between the cars is,
\[D = {d_1} + {d_2} = h\left( {\cot \alpha + \cot \beta } \right)\,yd\]
| \(\therefore\) The distance between the cars is\(= h\left( {\cot \alpha + \cot \beta } \right)\,yd\) |
Interactive Questions
Here are a few activities for you to practice. Select/Type your answer and click the "Check Answer" button to see the result.
Let's Summarize
This mini-lesson targeted the fascinating concept of heights and distances. The math journey around the heights and distances starts with what a student already knows, and goes on to creatively crafting a fresh concept in the young minds. Done in a way that not only it is relatable and easy to grasp, but also will stay with them forever. Here lies the magic with Cuemath.
About Cuemath
At Cuemath, our team of math experts is dedicated to making learning fun for our favorite readers, the students!
Through an interactive and engaging learning-teaching-learning approach, the teachers explore all angles of a topic.
Be it problems, online classes, doubt sessions, or any other form of relation, it’s the logical thinking and smart learning approach that we, at Cuemath, believe in.
Frequently Asked Questions
1. How do you find the distance in trigonometry?

\(\text{B (distance)} = \dfrac {\text{A (height)}} {\text{tan (e)}}\)
Therefore, to calculate \(B\) (distance) we will need the value of \(A\) (height) and angle \(e\).
2. What is an angle of depression in trigonometry?
If a person stands and looks down at an object, the angle of depression is the angle between the horizontal line of sight and the object.
3. What is the formula for the angle of depression?
If a person stands and looks down at an object, the angle of depression is the angle between the horizontal line of sight and the object.
4. Is the angle of elevation equal to depression?
An angle of elevation of one location relative to another is always congruent (equal in measure) to the angle of depression of the first location relative to the second.
5. What is the angle of sight in trigonometry?
The angle of elevation of an object as seen by an observer is the angle between the horizontal and the line from the object to the observer's eye (the line of sight).
6. What is the relationship between height and distance?

Using trigonometry, if we are provided with any of the two quantities that may be a side or an angle, we can calculate all the rest of the quantities. By the law of alternate angles, the angle of elevation and angle of depression are consequently equal in magnitude (α = β). Tan α is equal to the ratio of the height and distance.
7. What type of triangle is used to calculate heights and distances?
A right-angled triangle is used to calculate heights and distances.
8. What is the angle of elevation example?

- Live one on one classroom and doubt clearing
- Practice worksheets in and after class for conceptual clarity
- Personalized curriculum to keep up with school
