Alternate Interior Angles Theorem
Alternate Interior Angles theorem states, if two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent. Alternate interior angles are the angles formed on the opposite sides of the transversal. The alternate interior angles can prove whether the given lines are parallel or not. Let us learn more about the alternate interior angles theorem, the proof, and solve a few examples.
What is the Alternate Interior Angles Theorem?
The alternate interior angles theorem states that if a transversal crosses the set of parallel lines, the alternate interior angles are congruent. In the figure given below, a set of parallel lines m and n are intersected by the transversal and the following pairs of alternate interior angles are formed: ∠1 and ∠2, ∠3 and ∠4.
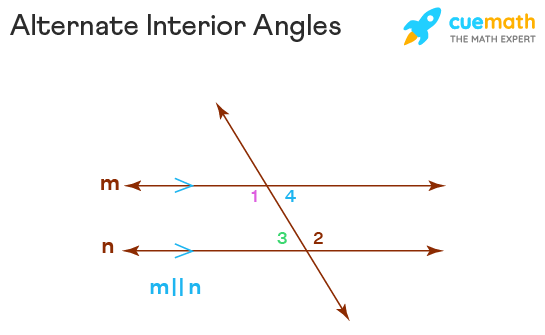
Since the given lines m and n are parallel, therefore the alternate interior angles will be congruent. ∠1 = ∠2 and ∠3 = ∠4.
Interior angles on the same side of the transversal are called consecutive interior angles or co-interior angles in short. Co-interior angles are supplementary when the lines are parallel.
∠2 + ∠3 = 180° and ∠6 +∠7 = 180°

Corresponding angles are a pair of angles on the similar corners of each of two lines on the same side of the transversal line. Corresponding angles formed by two parallel lines and a transversal are equal. Corresponding angles in the above image are: ∠2 and ∠4, ∠1 and ∠3, ∠5 and ∠7, and ∠6 and ∠8.
Definition of Alternate Interior Angles
When two parallel lines are crossed by a transversal, the pair of angles formed on the inner side of the parallel lines, but on the opposite sides of the transversal are called alternate interior angles. Alternate angles are of two types: Alternate interior angles and Alternate exterior angles
- Alternate interior angles: Alternate interior angles are the angles formed when a transversal intersects two coplanar lines. They are on the inner side of the coplanar lines but are on the alternate opposite sides of the transversal.
- Alternate exterior angles: Alternate exterior angles are formed on the exterior of the coplanar lines but on the alternate opposite sides of the transversal.
According to the image below:

Alternate interior angles are: ∠3 and ∠6, ∠4 and ∠5.
Alternate exterior angles are: ∠1 and ∠8, ∠2 and ∠7.
For example: Let us try to spot alternate interior angles in the given figure. Remember the lines do not have to be always parallel for alternate angles to be formed.

Alternate interior angles are: ∠3 and ∠6, ∠4 and ∠5
Alternate exterior angles are: ∠1 and ∠8, ∠2 and ∠7
Properties of Alternate Interior Angles
Here are a few properties of the alternate interior angles:
- The angles are congruent.
- Two lines that never intersect, are equidistant, and are coplanar are called parallel lines. The symbol for parallel to is II.
- If we have two lines (they don't have to be parallel) and have a third line that crosses them, then the crossing line is said to be a transversal.
- The sum of the angles formed on the same side of the transversal which are inside the two parallel lines is always equal to 180°.
- In the case of non – parallel lines, alternate interior angles don’t have any specific properties.
Finding Alternate Interior Angles
For finding alternate interior angles, we use the Z test. Make a zig-zag line including the parallel lines as shown in the diagram. Here, p and q are alternate interior angles. Similarly, a and d are also alternate interior angles.

Alternate Interior Angles Theorem and Proof
Statement: The theorem states that if a transversal intersects parallel lines, the alternate interior angles are congruent.
Given: Line p II line q
To prove: ∠2= ∠7 and ∠3 = ∠6

Proof: Suppose p and q are two parallel lines and t is the transversal that intersects p and q.
We know that, if a transversal intersects any two parallel lines, the corresponding angles and vertically opposite angles are congruent.
Therefore,
∠1 = ∠3 ………..(i) [Corresponding angles]
∠1 = ∠6 ………..(ii) [Vertically opposite angles]
From equations (i) and (ii), we get-
∠3 = ∠6 ..................[Alternate interior angles]
Similarly,
∠2 = ∠7
Hence, it is proved.
Alternate Interior Angles Theorem Converse
The converse of alternate interior angles theorem states that if two lines are intersected by a transversal forming congruent alternate interior angles, then the lines are parallel. Thus according to the converse of alternate interior angles theorem, the below-given lines will be parallel if ∠D is 40° and ∠B is 140°. This is because their corresponding alternate interior angles are of the measure 40° and 140°.

In conclusion, the alternate interior angles theorem states that the alternate interior angles will be equal if the lines are parallel, whereas its converse states that lines will be parallel if the alternate interior angles are congruent.
Co-interior Angles Theorem and Proof
Co-interior angles are the two interior angles that are on the same side of the transversal which makes it supplementary and sums up to 180 degrees. The co-interior angles resemble the shape C due to the placement of the angles but the angles are not equal to each other. The other names for co-interior angles are consecutive interior angles or the same side interior angles. The image below shows the shape of co-interiors.

Theorem: If the transversal intersects the two parallel lines, each pair of co-interior angles sums up to 180 degrees (supplementary angles).
Proof:
Let us consider the image given below:

In the figure, angles 3 and 5 are the co interior angles and angles 4 and 6 are the co-interior angles.
To prove: ∠3 and ∠5 are supplementary and ∠4 and ∠6 are supplementary.
Given that, a and b are parallel to each other and t is the transversal.
By the definition of linear pair,
∠1 and ∠3 form the linear pair.
Similarly, ∠2 and ∠4 form the linear pair.
By using the supplement postulate,
∠1 and ∠3 are supplementary
(i.e.) ∠1 + ∠3 = 180
Similarly,
∠2 and ∠4 are supplementary
(i.e.) ∠2 + ∠4 = 180
By using the corresponding angles theorem, we can write
∠1 ≅∠5 and ∠2 ≅ ∠6
Thus, by using the substitution property, we can say,
∠3 and ∠5 are supplementary and ∠4 and ∠6 are supplementary.
Hence, the co-interior angle theorem (consecutive interior angle) is proved.
The converse of this theorem is if a transversal intersects two lines, such that the pair of co-interior angles are supplementary, then the two lines are parallel.
Related Topics
Listed below are a few interesting topics related to the alternate interior angles theorem, take a look.
Examples on Alternate Interior Angles Theorem
-
Example 1: Cathy has been asked to find the pairs of alternate interior angles from the given diagram. Can you help her?

Solution: The alternate interior angles lie on "alternate" sides of the transversal, and they must be in the "interior" of the two parallel lines. The alternate interior angles are: ∠q and ∠z, ∠r and ∠a.
-
Example 2: Julia asks her students if they can find the relationship between \(\angle q\) and \(\angle d\) if the given lines \(m\) and \(n\) are parallel. Can you tell how are \(\angle q\) and \(\angle d\) related to each other?

Solution: The given lines are parallel and are intersected by a transversal.
According to the alternate interior angles theorem, the two congruent alternate interior angles are produced. They are: ∠q and ∠d,∠c and ∠p.
Therefore, ∠q and ∠d are congruent alternate interior angles.
-
Example 3: If the given two lines are parallel and are intersected by a transversal, what will be the measure of ∠X and ∠Y?

Solution: The given lines are parallel and according to the alternate interior angles theorem, the given angle of measure 85° and ∠X are congruent alternate interior angles.
Therefore, 85° = ∠X
Similarly, 95° and Y are congruent alternate interior angles. Therefore, 95° = ∠Y.

FAQs on Alternate Interior Angles Theorem
What is the Alternate Interior Angles Theorem?
The alternate interior angles theorem states that if a transversal crosses the set of parallel lines, the alternate interior angles are congruent. Two lines that never intersect, are equidistant, and are coplanar are called parallel lines. The symbol for parallel to is II. If we have two lines (they don't have to be parallel) and have a third line that crosses them, then the crossing line is said to be a transversal.
What is the Converse of the Alternate Interior Angles Theorem?
According to the converse of the alternate interior angles theorem, if a transversal intersects two lines such that the alternate interior angles are equal, then the two lines are said to be parallel.
Are Alternate Interior Angles Congruent?
Yes, alternate interior angles are congruent.
How is the Alternate Interior Angles Theorem and the Alternate Exterior Angles Theorem Alike?
The alternate interior angles theorem states that if two parallel lines are cut by a transversal, then the alternate interior angles are congruent. The alternate exterior angles theorem states that if two parallel lines are cut by a transversal, then the alternate exterior angles are congruent. Thus, the two theorems are alike with respect to the congruent angles produced.
visual curriculum