Pairs of Angles

When angles appear in groups of two to display a certain geometrical property they are termed as pairs of angles. There is a special relationship between pairs of angles. Some of the angle pairs include complementary angles, supplementary angles, vertical angles, alternate interior angles, alternate exterior angles, corresponding angles, adjacent angles. In this article, we will read about different pairs of angles with the help of infographic images and interesting solved examples.

When two lines intersect each other, the adjacent angles make a linear pair. The sum of linear pairs is 180°. It should be noted that all linear pairs are supplementary because supplementary angles sum up to 180°. However, all supplementary angles need not be linear pairs because in linear pairs the lines need to intersect each other to form adjacent angles. In the following figure, ∠1 and ∠2 form a linear pair and their sum is equal to 180°.

Any two angles that share a common side, a common vertex, and that do not overlap are called adjacent angles. In the following figure, ∠1 and ∠2 are adjacent angles.

When two lines intersect, the angles opposite to each other are equal and are called vertical angles or vertically opposite angles. In the following figure, ∠1 and ∠2 are equal, and ∠3, and ∠4 equal because they are vertically opposite angles.

When the sum of two angles is 90°, the angles are called complementary angles. Each angle is called the complement of the other angle. In the figure given below, ∠AOB + ∠BOC = 90° ⇒ 20° + 70° = 90°.
Thus, ∠AOB and ∠BOC are complementary angles.

Two angles are considered supplementary when they sum up to 180°. It is not necessary that the angles must always be adjacent to each other, as in the case of linear pairs. In other words, all linear pairs are supplementary, but all supplementary angles need not be linear pairs. However, the sum of the angles in both the cases should always be 180°. When two angles are supplementary angles each angle is called the supplement of the other angle.

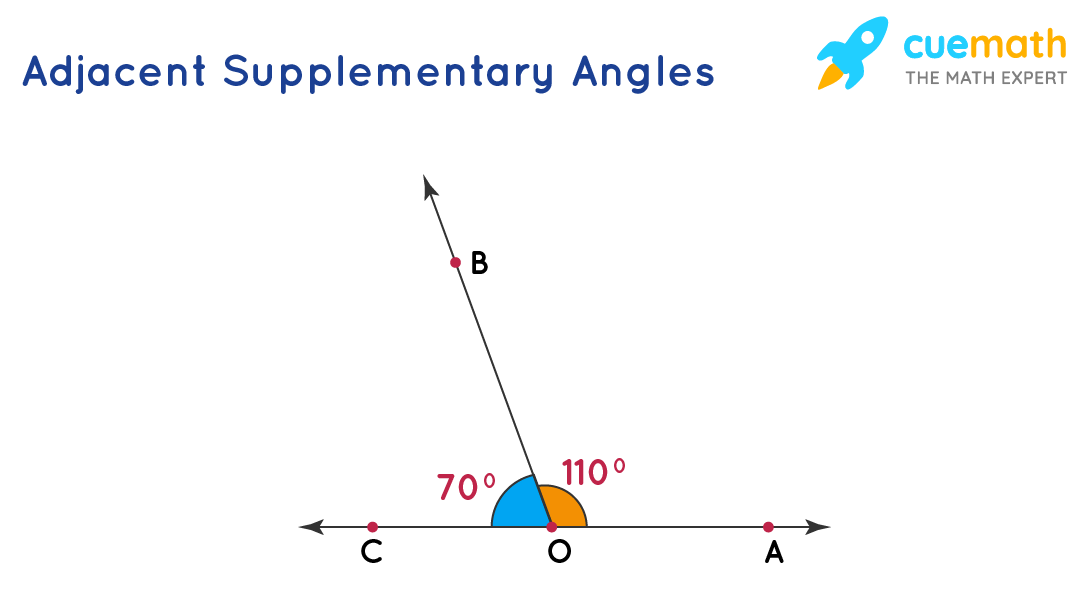
∠BOC + ∠BOA = 180°

∠ABC + ∠PQR = 180°

When 2 parallel lines are cut by a transversal, many pairs of angles are formed. These pair of angles have a special relationship between them. Let us discuss the pairs of angles formed by a transversal in detail.

Co-interior Angles

When a transversal intersects two parallel lines, the co-interior angles are always supplementary. Co-interior angles are those angles that:

• Have different vertices.
• Lie between two lines.
• Are on the same side of the transversal.

In the following figure, ∠3 and ∠6 are co-interior angles. Similarly, ∠4 and ∠5  are co-interior angles. Therefore, they are supplementary.

Alternate Interior Angles

When a transversal intersects two parallel lines, the alternate interior angles formed are always equal. Alternate-interior angles are those angles that:

• Have different vertices.
• Lie on the alternate sides of the transversal.
• Lie between the interior of the two lines.

In the following figure, ∠4 and ∠6, ∠3 and ∠5 are the alternate interior angles.

Alternate Exterior Angles

When a transversal intersects two parallel lines, the alternate exterior angles formed are always equal. Alternate-exterior angles are those angles that:

• Have different vertices.
• Lie on the alternate sides of the transversal.
• Are exterior to the lines.

In the following figure, ∠1 & ∠7, ∠2 & ∠8  are alternate exterior angles.

Corresponding Angles

When a transversal intersects two parallel lines, the corresponding angles formed are always equal. Corresponding angles are the angles that:

• Have different vertices.
• Lie on the same side of the transversal, and lie above (or below) the lines

In the following figure, ∠1 and ∠2 are pairs of corresponding angles that are equal.

Important Notes

Read the following points to overcome some common mistakes and know the real facts behind them.

• Mistake: Complementary angles have to be next to each other.
• Fact: When the sum of two angles is 90°, the angles are called complementary angles. These angles need not be necessarily next to each other but their sum should be 90°.
• Mistake: Any angles next to each other are adjacent angles.
• Fact: For angles to be adjacent, they have to share a common side and vertex.
• Mistake: All supplementary angles are linear pairs.
• Fact: All linear pairs are supplementary, but all supplementary angles need not be linear pairs. However, the sum of the angles in both cases should always be 180°.

Related Articles on Pairs of Angles

Given below is the list of topics that are closely connected to Pairs of Angles. These topics will also give you a glimpse of how such concepts are covered in Cuemath.

• Angles
• Transversal and Related Angles
• Corresponding Angles
• Interior Angles
• Protractor
• Acute Angle
• Supplementary Angles
• Obtuse Angle
• Complementary Angles

How Many Pairs of Angles Are There?

There are nine pairs of angles listed below:

• Alternate Interior Angles
• Alternate Exterior Angles
• Co-interior Angles
• Complementary Angles
• Supplementary Angles
• Adjacent Angles
• Vertical Angles
• Corresponding Angles
• Linear Pair of Angles

How Many Pairs of Angles are Supplementary?

Two angles are considered supplementary when they sum up to 180°. It is not necessary that the angles must always be adjacent to each other, but their sum should always be 180°. When two angles are supplementary angles each angle is called the supplement of the other angle.

What Pairs of Angles are Always Adjacent?

When the two angles share a common side, a common vertex, and they do not overlap, then the pairs of angles are always adjacent angles.

What are Linear Pairs of Angles?

When two lines intersect each other, the adjacent angles make a linear pair. The sum of linear pairs is 180°. It should be noted that all linear pairs are supplementary because supplementary angles sum up to 180°.

Which Pair of Angles are Alternate Interior Angles?

When two parallel lines are intersected by a transversal then alternate interior angles are angles formed. These alternate interior angles have different vertices, they lie on the alternate sides of the transversal and are in between the interior of the two lines.

How to Solve Linear Pairs of Angles?

When two angles form a linear pair and the measurement of one angle is given then it is easy to find the value of the other angle using the linear pairs of angles property. On subtracting the given angle from 180° we get the value of the other angle.