Corresponding Angles
Corresponding angles are the angles that are formed when two parallel lines are intersected by the transversal. The opening and shutting of a lunchbox, solving a Rubik's cube, and never-ending parallel railway tracks are a few everyday examples of corresponding angles. These are formed in the matching corners or corresponding corners with the transversal.
| 1. | What are Corresponding Angles? |
| 2. | How to Find Corresponding Angles? |
| 3. | Corresponding Angles Theorem |
| 4. | FAQs on Corresponding Angles |
What are Corresponding Angles?
The corresponding angles definition tells us that when two parallel lines are intersected by a third one, the angles that occupy the same relative position at each intersection are known to be corresponding angles to each other.
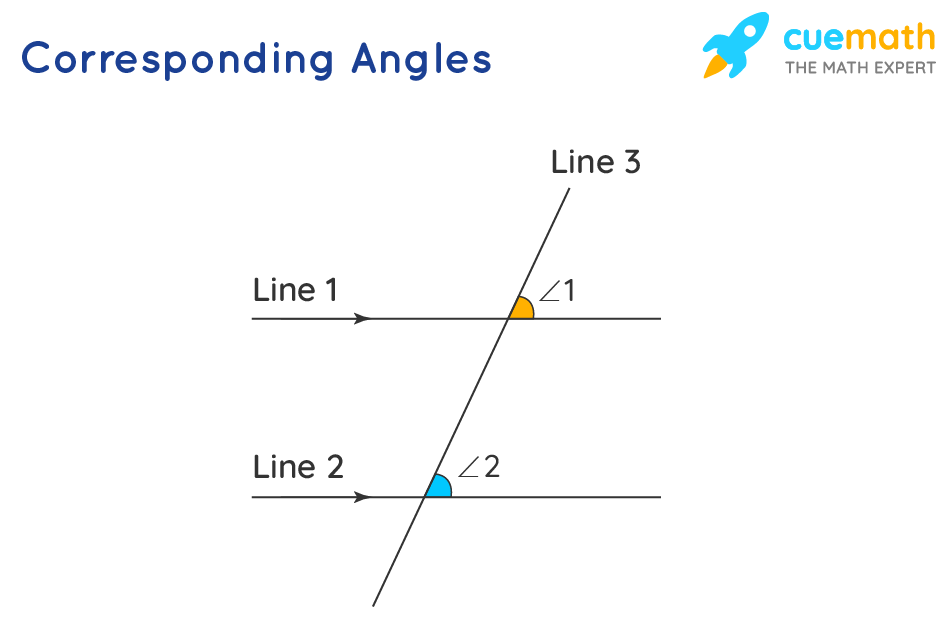
According to geometry, and the definition of the corresponding angles, we can say that:
- Lines 1 and 2 are parallel. Thus, we have two parallel lines
- Line 3 is intersecting lines 1 and 2. Thus, we have intersected parallel lines
- From the diagram, we can see that angles 1 and 2 are occupying the same relative position - the upper right side angles in the intersection region.
Hence, our corresponding angles definition seems to be justified. Therefore, we can say that angles 1 and 2 are corresponding angles.
Now that we have understood the definition of corresponding angles, we can figure out whether any two given angles are corresponding or not in any given diagram. The word “corresponding” itself suggests that the angles can be either inequivalent or equivalent (congruent). Surprisingly, corresponding angles formed by the transversal that intersects two parallel lines are angles that are congruent. When the transversal intersects two non-parallel lines, the corresponding angles are not congruent.
How to Find Corresponding Angles?
We know that each intersection point has 4 angles. Now, each of the four angles in the first intersection region will have another one with the same relative position in the second intersection region.
Now, we will separate each of these four angles into different categories. Look at the table below to get a better understanding of the different types of corresponding angles.
| Name of Angles | Location |
|---|---|
| Angles 1 and 5 | Upper Right Side Angle |
| Angles 2 and 6 | Upper Left Side Angle |
| Angles 3 and 7 | Lower Right Side Angle |
| Angles 4 and 8 | Lower Left Side Angle |
Corresponding Angles Theorem
According to the corresponding angles theorem, the statement “If a line intersects two parallel lines, then the corresponding angles in the two intersection regions are congruent” is true either way.
The Converse of Corresponding Angles Theorem
The corresponding angles converse theorem would be, “If the corresponding angles in the two intersection regions are congruent, then the two lines are said to be parallel.
What if a transversal intersects two parallel lines and the pair of corresponding angles are also equal? Then, the two lines intersected by the transversal are said to be parallel. This is the converse of the corresponding angle theorem.
Important Notes on Corresponding Angles
- When two parallel lines are intersected by a third one, the angles that occupy the same relative position at each intersection are called corresponding angles to each other.
- Corresponding angles are congruent to each other.
- If the corresponding angles in the two intersection regions are congruent, then the two lines are said to be parallel.
Challenging Question on Corresponding Angles
The following information has been given regarding angles A, B, C, and D :
- A and B are corresponding angles
- B and C are supplementary angles
- C and D are co - interior angles
Find the angle (other than B), which will be congruent to angle A.
Corresponding Angles Examples
-
Example 1: Have you ever noticed a tall building? In most tall buildings, each of its floors is designed in exactly the same way, especially the walls of the house on each floor. Compare the corresponding angles in such a case.
Solution:
Let us consider the bottom tiles of floor 1 as line 1 and that of floor 2 as line 2. Now, we know that line 3 is intersecting lines 1 and 2. In this figure, you can notice the geometry of the corresponding angles.
Can you see any similarity between angles 1 and 2? You can see that angles 1 and 2 are corresponding angles. Not only that, as all the floors are always built parallel to each other, we can say that lines 1 and 2 are parallel.
Therefore, ∠1 is corresponding to ∠2
-
Example 2: Did you ever notice the parallel lines on a railway track? There are multiple intersections of different smaller lines with the two main parallel track lines. Compare the angles made by the intersection.
Solution:
Can you see any similarity between the concept of congruent angles and angles 1 and 2 in the diagram given below? Recall the definition we used for corresponding angles to fit into our angles shown here.
You will be able to see that if we consider the track lines to be parallel, angles 1 and 2 can be considered as corresponding angles. This is according to the corresponding angles in the Math definition. Thus, if angle 1 is 90 degrees then angle 2 will also be equal to 90 degrees.
Therefore, ∠1 s corresponding to ∠2 and angle 1 = angle 2 = 90 degrees.
-
Example 3: Have you ever come across two parallel streets? There is usually a connecting road between the two streets that also intersects it. Now, try to relate the angles made by the street at each intersection point with the two parallel roads.
Solution:
Apply our definition for corresponding angles to the angles shown here. You will see that according to our definition, these angles are corresponding!
Not only that, as all the streets are always built parallel to each other, we can also say that angles residing on the same relative positions on the streets will always be corresponding angles.
Therefore, Angles formed by parallel streets are corresponding angles.
FAQs on Corresponding Angles
What are Corresponding Angles in Geometry?
Corresponding angles in geometry are defined as the angles which are formed at corresponding corners with the transversal. When the two parallel lines are intersected by the transversal it forms the pair of corresponding angles.
☛ To know more about corresponding angles check now:
What are the Two Types of Corresponding Angles?
According to the definition of the corresponding angles, we can classify corresponding angles further into two types listed below:
- Corresponding angles - by transversal and parallel lines: Corresponding angles formed are congruent.
- Corresponding angles - by transversal non-parallel lines: Corresponding angles formed are not equal.
☛ Check Corresponding Angles Worksheets now for more practice.
Do Corresponding Angles Add Up to 180?
Yes, corresponding angles can add up to 180. In some cases when both angles are 90 degrees each, the sum will be 180 degrees. These angles are known as supplementary corresponding angles.
☛ Check Supplementary angles now for more clarification.
What are Alternate and Corresponding Angles?
Alternate angles are angles that are at relatively opposite positions to each other; while the corresponding angles are the angles that are at relatively same positions to each other.
Can Corresponding Angles be Consecutive Interior Angles?
No corresponding angles can not be considered as consecutive interior angles because the consecutive interior angles are the angles that are on the same side of the transversal but inside the two parallel lines.
Can Corresponding Angles be Right Angles?
If the transversal is perpendicular to the given parallel lines, then the corresponding angles of a transversal across parallel lines are right angles, all angles are right angles.
☛ Check Supplementary angles now for better understanding.
What do Corresponding Angles Look Like?
When two parallel lines are intersected by a transversal, the angles so formed occupying the same relative position at each intersection are corresponding angles. When two parallel lines are crossed by a transversal, then the angles in the same corners of each line are said to be corresponding angles and the transversal will look like a straight line.
What do you Understand by Corresponding Angles Postulate?
According to the corresponding angles postulate, the corresponding angles are congruent if the transversal intersects two parallel lines.
What is the Converse of Corresponding Angles Postulate?
We just read that the corresponding angles postulate states that the corresponding angles are congruent if the transversal intersects two parallel lines. Whereas converse of corresponding angles postulates says, if the corresponding angles in the two intersection regions are congruent, then the two lines are said to be parallel.
Are Corresponding Angles Sum up to 90 Degrees?
If the corresponding angles are equal then in some cases when both angles are 45 degrees each, the sum will be 90 degrees. These angles are known as complementary corresponding angles.
☛ Check complementary angles now for more details.