Supplementary Angles
Supplementary angles refer to the pair of angles that always sum up to 180°. The word 'supplementary' means 'something when supplied to complete a thing'. Therefore, these two angles are called supplements of each other.
Let us learn more about the definition and meaning of supplementary angles along with some supplementary angles examples. We will also learn the difference between complementary angles and supplementary angles.
What are Supplementary Angles?
Two angles are said to be supplementary angles if they add up to 180°. Supplementary angles form a straight angle (180°) when they are put together.
Definition of Supplementary Angles
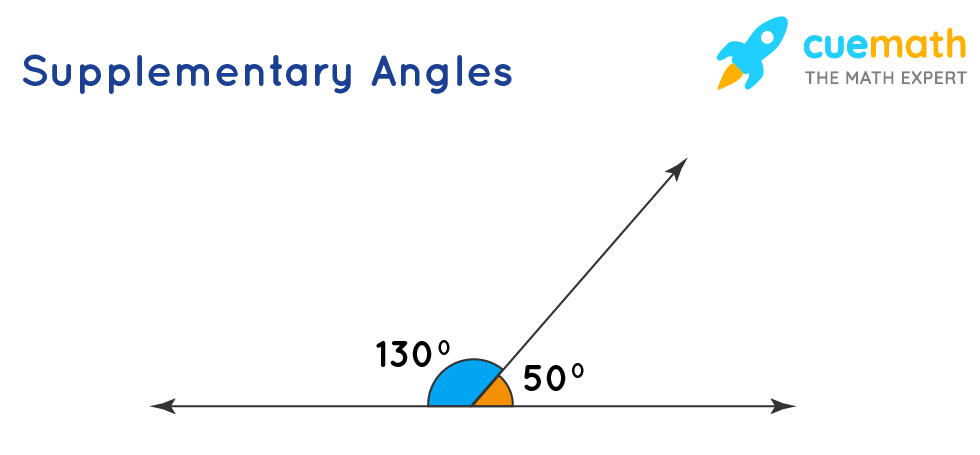
Any two angles that sum up to 180° are called supplementary angles. Observe the following figure which shows two angles 130° and 50° and since they add up to 180°, they are called supplementary angles. In other words, angle 1 and angle 2 are supplementary, if Angle 1 + Angle 2 = 180°. In this case, Angle 1 and Angle 2 are called 'supplements' of each other. Hence, by the definition of supplementary angles, these two angles are supplementary.
Adjacent and Non-Adjacent Supplementary Angles
Supplementary angles can either be adjacent or non-adjacent. So, there are two types of supplementary angles. Each of these types of supplementary angles is explained below.
- Adjacent supplementary angles
- Non-adjacent supplementary angles
Adjacent Supplementary Angles
Two supplementary angles with a common vertex and a common arm are said to be adjacent supplementary angles.
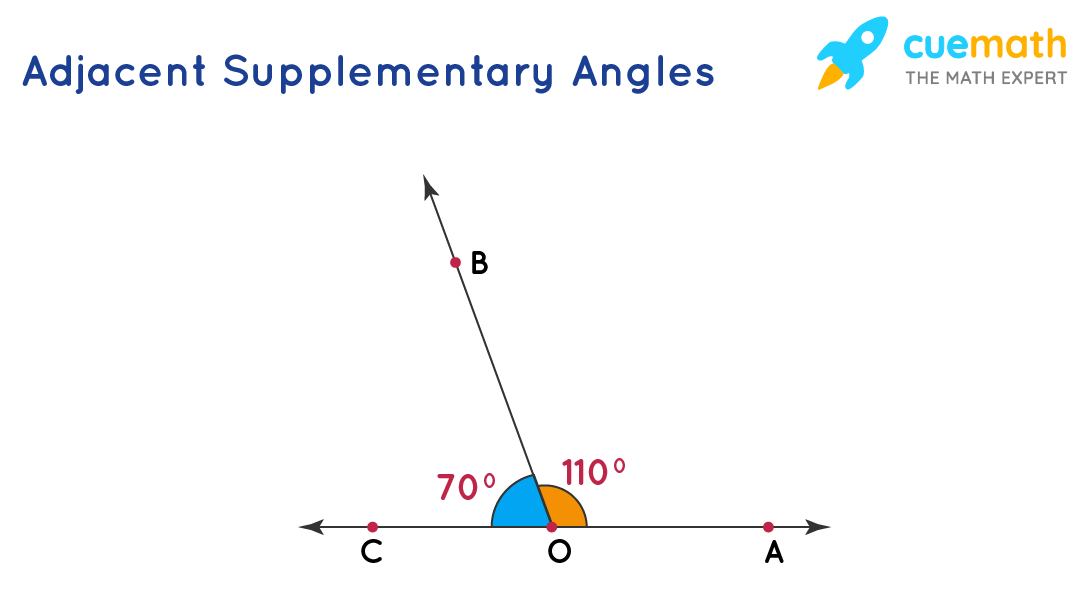
Observe the figure given below which shows that ∠COB and ∠AOB are adjacent angles as they have a common vertex, O, and a common arm OB. They also add up to 180°, that is, ∠COB + ∠ AOB = 70° + 110° = 180°. Hence, these two angles are adjacent supplementary angles.
Non-adjacent Supplementary Angles
Two supplementary angles that are NOT adjacent are said to be non-adjacent supplementary angles. They may add up to 180° but they do not share any common vertex or common arm.
Observe the figure given below which shows ∠ABC and ∠PQR are non-adjacent angles as they neither have a common vertex nor a common arm. They also add up to 180°, that is, ∠ABC+ ∠PQR = 79° + 101° = 180°. Hence, these two angles are non-adjacent supplementary angles. Non-adjacent supplementary angles, when put together, form a straight angle.

Complementary and Supplementary Angles
Complementary angles and supplementary angles are those angles that exist in pairs. While supplementary angles add up to 180°, complementary angles add up to 90°. These angles have numerous real-time applications, the most common being the crossroads. The following table shows the difference between supplementary and complementary angles.
The supplementary vs complementary angles table.
|
Complementary Angles |
Supplementary Angles |
|---|---|
|
Two angles are said to be complementary if they add up to 90°. |
Two angles are said to be supplementary if they add up to 180° |
|
Complement of an angle x is (90 - x)° |
Supplement of an angle x is (180 - x)° |
Tips on Supplementary angles vs Complementary angles
Here is a little trick for you to remember the difference between supplementary angles and complementary angles.
- 'S' is for 'Supplementary' and 'S' is for 'Straight'. Hence, you can remember that two 'Supplementary' angles when put together form a 'Straight' angle.
- 'C' is for 'Complementary' and 'C' is for 'Corner'. Hence, you can remember that two 'Complementary' angles when put together form a 'Corner (right)' angle.
How to find the Supplement of an Angle?
When the sum of two angles is equal to 180°, then we call that pair of angles, supplements of each other. So, we know that the sum of two supplementary angles is 180°, and each of them is said to be a 'supplement' of the other. Thus, the supplement of an angle is found by subtracting it from 180°. This means the supplement of x° is (180 - x)°
Example: Find the supplement of 86°
Solution: The supplement of 86° is obtained by subtracting it from 180°. This means 180° - 86° = 94°. Therefore, the supplement of 77° is 103°
☛ Related Articles
Supplementary Angles Examples
-
Example 1:
Find the value of angle Y in the following figure.

Solution:
In the given figure, Y and 77° are supplementary angles as they lie at a point on a straight line. Hence, their sum is 180°.
Y + 77° = 180°
Y = 180° - 77° = 103°
Therefore, Y = 103°
-
Example 2:
Find the values of Angle A and Angle B, if they are supplementary angles such that ∠A = (2x + 10)° and Angle B = (6x − 46)°
Solution:
Since Angle A and Angle B are supplementary angles, their sum is 180°
∠A + ∠B = 180°
(2x + 10) + (6x - 46) = 180°
8x - 36 =180
8x = 216
x = 27
Therefore, Angle A = 2(27) + 10 = 64° and Angle B = 6(27) - 46 =116°
-
Example 3:
Find the value of x if the following two angles are supplementary.

Solution:
Since the given angles are supplementary, their sum is 180°.
x/2 + x/3 =180°
5x/6 =180°
x =180° × 6/5 = 216°
Therefore, the value of x is 216°. This means one angle is 216/2 = 108° and the other angle is 216/3 = 72°.
They can be verified as supplementary angles because their sum is 180°, that is, 108° + 72° = 180°

FAQs on Supplementary Angles
What is the Meaning of Supplementary Angles in Geometry?
In geometry, two angles are said to be supplementary angles if they add up to 180°. For example, if ∠A + ∠B = 180°, then ∠A and ∠B are called supplementary angles. Supplementary angles always form a straight angle (180°) when they are put together.
Can Two Acute Angles be Supplementary Angles?
No, if two angles are supplementary, then they are both either right angles or one of them is acute and one of them is obtuse. If two acute angles are put together, their sum will always be less than 180°, so two acute angles can never be supplementary angles. For example, let us take two acute angles 70° and 50°, if we add them we get 120°. Similarly, we can check for other acute angles and conclude that two acute angles cannot be supplementary.
Can Two Obtuse Angles be Supplementary Angles?
No, if two angles are supplementary, then they are both either right angles or one of them is acute and one of them is obtuse. If two obtuse angles are put together, their sum will always be greater than 180°, so two obtuse angles can never be supplementary angles. For example, let us take two obtuse angles 110° and 130°, if we add them we get 240°. Similarly, we can check for other obtuse angles and conclude that two obtuse angles cannot be supplementary.
Can Two Right angles be Supplementary Angles?
Yes, two right angles are always supplementary because 90° + 90° = 180°.
Are Supplementary and Complementary Angles the Same?
No, supplementary and complementary angles are not the same. Two angles form a pair of complementary angles when their sum is 90°, whereas, two angles form a pair of supplementary angles when their sum is 180°.
Can Three Angles be Supplementary?
No, three angles can never be supplementary even if their sum is 180°. Though the sum of angles, 40°, 90°, and 50° is 180°, they are not supplementary angles because supplementary angles always occur in pairs. The definition of supplementary angles holds true only for two angles.
What Angle is Supplementary to 84 Degrees?
The supplement of an angle is obtained by subtracting it from 180°. Thus, the angle that is supplementary to 84° is 180° - 84° = 96°.
What Angle is Formed if we Put the Supplementary Angles Together?
When a pair of supplementary angles are put together, they form a straight angle.
What are Adjacent Supplementary Angles?
Adjacent supplementary angles are those angles that share a common arm and a common vertex and they always sum up to 180°.
What is the Sum of Two Supplementary Angles?
The sum of two supplementary angles is always 180°. Supplementary angles may be adjacent angles or non-adjacent angles but they always add up to 180°.
How to Identify Supplementary Angles?
Supplementary angles can be easily identified by their sum. If any two angles add up to 180°, they are supplementary angles.
Can Two Adjacent Angles be Supplementary?
Yes, two adjacent angles can be supplementary if they form a straight line together. However, all adjacent angles may not always necessarily be supplementary because the definition of adjacent angles says that adjacent angles are those angles that share a common side and a common vertex, but their sum may not always necessarily be 180°.
How to Find Supplementary Angles?
When two angles are supplementary and we know the value of one angle, we can find the value of the other angle by subtracting the given angle from 180° because supplementary angles always add up to 180°. For example, if we need to find the supplement of 60°, we will subtract 180° - 60° = 120°.
What do Supplementary Angles Add up to?
Supplementary angles always add up to 180deg;. This means if any two angles add up to 180°, they are called supplementary angles.
visual curriculum