Common Multiples
Common multiples are the multiples that are shared by a given set of numbers. For example, in order to find the common multiples of 3 and 6, we list the multiples of 3 and 6 separately and then find the multiples that are common in both the lists. The multiples of 3 can be listed as 3, 6, 9, 12, 15, 18, and so on. The multiples of 6 can be listed as 6, 12, 18, 24, 30, 36, 42, and so on. Now, if we find the multiples that are common in both the lists, we get 6, 12, and 18. These are termed as the common multiples of 3 and 6.
| 1. | Common Multiples Definition |
| 2. | How To Find Common Multiples? |
| 3. | Common Multiples of Two Numbers |
| 4. | Common Multiples of Three Numbers |
| 5. | Least Common Multiple |
| 6. | FAQs on Common Multiples |
Common Multiples Definition
The multiples that are common to two or more numbers are termed as the common multiples of the given numbers. Before understanding more about common multiples, let us recollect what multiples mean. When we multiply a number by counting numbers, we get its multiples. This means that we can get the multiples of 4 by multiplying 4 with the numbers 1, 2, 3.... and so on. For example, if we say 4 × 5 = 20, here, 20 is a multiple of 4 and 5. The other multiples of 4 can be listed as 4 (4 ×1 = 4), 8 (4 × 2 = 8), 12 (4 × 3 = 12), and so on.
The common multiples of two or more numbers are the numbers that can be completely divisible by each of the given numbers. For example, let us find the common multiples of 6 and 8. First, let us list the multiples of 6 and 8. If we observe the two lists, we find that 24 and 48 are their common multiples.
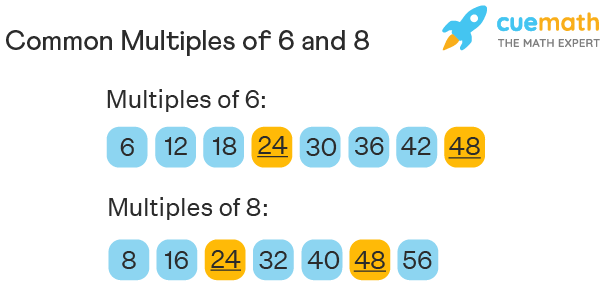
Thus, the common multiples of 6 and 8 can be listed as, 24, 48, and so on.
How to Find Common Multiples?
To find the common multiples for a given set of numbers, first, we need to list all the multiples of the given numbers and then start selecting the common multiples.
For example, the common multiples of 20 and 40 can be found out by listing the multiples of 20 and 40.
Multiples of 20 ⇒ 20, 40, 60, 80, 100, 120, 140, 160,...and so on.
Multiples of 40 ⇒ 40, 80, 120, 160, 200, 240, 280, 320,..and so on.
The common multiples of 20 and 40 are 40, 80, 120, 160,.....and so on.
Common Multiples of Two Numbers
The common multiples of two numbers can be easily found by listing their multiples. After listing the multiples of the given numbers, we can mark or circle the multiples that are shared by both the numbers. These are the common multiples of the two numbers. For example, let us find the common multiples of 2 and 5.
Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, ....
Multiples of 5: 5, 10, 15, 20, 25, 30,...
Therefore, the common multiples of 2 and 5 are: 10, 20, ...., and so on. It should be noted that all the common multiples are completely divisible by 2 and 5.
Common Multiples of Three Numbers
The common multiples of three numbers can be found in the same way as we find the common multiples of two numbers. The multiples that are shared by the given three numbers are their common multiples.
For example, let us find out the common multiples of 10, 20, and 30. If we observe, there are some multiples that are common in 10 and 20 but they are not present in the multiples of 30. So, they cannot be considered as the common multiples of all the three numbers. We need to select the multiples that are shared among all the three numbers.
Let us list the multiples of 10, 20, and 30 to get their common multiples.
Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120...and so on.
Multiples of 20: 20, 40, 60, 80, 100, 120, 140, 160, 180,.... and so on.
Multiples of 30: 30, 60, 90, 120, 150, 180, 210,.... and so on.
So the common multiples of 10, 20, and 30 are 60 and 120,..... and so on.
Least Common Multiple
The least common multiple is the smallest number that is the product of two or more numbers. In other words, it is the lowest possible number that can be divisible by the given numbers. The least common multiple (LCM) of numbers can be calculated by various methods like the listing method, the prime factorization method, and the division method. Let us find the LCM of 3 and 7 by the listing method.
Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42,...
Multiples of 7: 7, 14, 21, 28, 35, 42, 49,.....
We can see that the common multiples of 3 and 7 are 21, 42, and so on. Among these common multiples, the least multiple is 21. Therefore, the LCM of 3 and 7 is 21 because it is the smallest among all the common multiples. So, the LCM of 3 and 7 is 21.
Related Articles on Common Multiples
Check out these interesting articles to know more about common multiples and its related topics.
FAQs on Common Multiples
What are Common Multiples?
Common multiples are the multiples that are common to two or more given numbers. For example, let us find the common multiples of 4 and 6. The multiples of 4 can be listed as 4, 8, 12, 16, 20, 24, and so on. The multiples of 6 can be listed as 6, 12, 18, 24, 30, 36, 42, and so on. Now, if we find the multiples that are common in both the lists, we get 12 and 24. These are termed as the common multiples of 4 and 6.
How to find the Common Multiples of Two Numbers?
We can find out the common multiples of two numbers by listing the multiples of the given numbers and then select the common multiples among them.
For example, in order to find the common multiples of 2 and 3, we will first write the multiples of 2 and 3.
Multiples of 2 ⇒ 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24,....
Multiples of 3 ⇒ 3, 6, 9, 12, 15, 18, 21, 24,......
Now, if we observe these multiples, we find that the common multiples of 2 and 3 are 6, 12, 18, 24,...and so on.
What are the Common Multiples of 3 and 4?
The common multiples of 3 and 4 can be found by writing the multiples of 3 and 4. Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24,......and so on. Multiples of 4: 4, 8, 12, 16, 20, 24,... and so on. The common multiples in these two lists are 12, 24... and so on.
What are Least Common Multiples?
The least common multiple is the smallest number that is the product of two or more numbers. In other words, it is the lowest possible number that is divisible by the given numbers. The least common multiple (LCM) of numbers can be calculated by various methods like the listing method, the prime factorization method, and the division method. Let us find the least common multiple (LCM) of 5 and 6 by the listing method.
Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60....
Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60,...
The common multiples of 5 and 6 are 30 and 60,...and so on. Among these common multiples, the smallest multiple is 30. Therefore, the LCM of 5 and 6 is 30 because it is the least among all the common multiples.
How to find the Common Multiples of Three Numbers?
The common multiples of three numbers can be calculated in the same way as we find the common multiples of two numbers. The multiples that are shared by the given three numbers are their common multiples. For example, let us find the common multiples of 2, 3 and 6.
Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24,.....,....and so on
Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24,..........and so on
Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48,...and so on
The common multiples of 2, 3, and 6 are 6, 12, 18, 24,...and so on. Among these common multiples, the smallest multiple is 6. Therefore, the LCM of 2, 3, and 6 is 6 because it is the least among all the common multiples. So, the LCM of 2, 3, and 6 is 6.
What are the Common Multiples of 12 and 18?
In order to find the common multiples of 12 and 18, we will first write the multiples of 12 and 18. Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144, ... and so on. Multiples of 18: 18, 36, 54, 72, 90, 108, 126, 144, and so on. Among these, the multiples that are common in the lists are 36, 72, 108, 144, and so on.
What is the Least Common Multiple of 8 and 12?
The Least Common Multiple of 8 and 12 is 24. The following steps show the procedure to calculate the least common multiple of 8 and 12.
- Write down the multiples of 8. They are 8, 16, 24, 32, 40, 48, 56, 64, 72.... and so on.
- Write down the multiples of 12. They are 12, 24, 36, 48, 60, 72, 84... and so on.
- Now, list the common multiples of 8 and 12: 24, 48, 72, and so on. Among these, the smallest multiple is 24.
- Therefore, the least common multiple (LCM) of 8 and 12 is 24.
What are the First Three Common Multiples of 3 and 6?
First, let us find out the multiples of 3 and 6.
- Multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24,... and so on.
- Multiples of 6 are 6, 12, 18, 24, 30, 36,... and so on.
Therefore, the first three common multiples of 3 and 6 are 6, 12, and 18.