HCF - Highest Common Factor

The Highest Common Factor (HCF) of two numbers is the highest possible number that divides both the numbers completely. The Highest Common Factor (HCF) is also called the Greatest Common Divisor (GCD).

There are many ways to find the HCF of two numbers. One of the quickest ways to find the HCF of two or more numbers is by using the prime factorization method. Explore the world of HCF by going through its various aspects and properties. Find answers to questions like what is the highest common factor for a group of numbers, easy ways to calculate HCF, HCF by division method, its relation with LCM, and discover more interesting facts around them.

1.	What is HCF?
2.	How to Find HCF?
3.	Relation Between LCM and HCF
4.	FAQs on HCF

The HCF (Highest Common Factor) of two or more numbers is the highest number among all the common factors of the given numbers. In simple words, the HCF (Highest Common Factor) of two natural numbers x and y is the largest possible number that divides both x and y. Let us understand this HCF definition using two numbers, 18 and 27. The common factors of 18 and 27 are 1, 3, and 9. Among these numbers, 9 is the highest (largest) number. So, the HCF of 18 and 27 is 9. This is written as: HCF (18, 27) = 9. Observe the following figure to understand this concept.

HCF Examples

Using the above HCF definition, the HCF of a few sets of numbers can be listed as follows:

• HCF of 60 and 40 is 20, i.e., HCF (60, 40) = 20
• HCF of 100 and 150 is 50, i.e., HCF (150, 50) = 50
• HCF of 144 and 24 is 24, i.e., HCF (144, 24) = 24
• HCF of 17 and 89 is 1, i.e., HCF (17, 89) = 1

There are many ways to find the highest common factor of the given numbers. Irrespective of the method, the answer to the HCF of the numbers is always the same. There are 3 methods to calculate the HCF of two numbers:

• HCF by listing factors method
• HCF by prime factorization
• HCF by division method

Let us discuss each method in detail with the help of examples.

HCF by Listing Factors Method

In this method, we list the factors of each number and find the common factors of those numbers. Then, among the common factors, we determine the highest common factor. Let us understand this method using an example.

Example: Find the HCF of 30 and 42.

Solution: We will list the factors of 30 and 42. The factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30 and the factors of 42 are 1, 2, 3, 6, 7, 14, 21, and 42. Clearly, 1, 2, 3, and 6 are the common factors of 30 and 42. But 6 is the greatest of all the common factors. Hence, the HCF of 30 and 42 is 6.

HCF by Prime Factorization

In order to find the HCF of numbers by the prime factorization method, we use the following steps. Let us understand this method using the example given below.

• Step 1: Find the common prime factors of the given numbers.
• Step 2: Then, multiply the common prime factors that have the least or smallest power to obtain the HCF of those numbers.

Example: Find the HCF of 60 and 90.

Solution:

The prime factors of 60 = 2 × 2 × 3 × 5 or 2² × 3 × 5

The prime factors of 90 = 2 × 3 × 3 × 5 or 2 × 3² × 5.

Now, the HCF of 60 and 90 will be the product of the common prime factors that have the least powers, which are, 2, 3, and 5. So, HCF of 60 and 90 = 2 × 3 × 5 = 30

HCF by Division Method

The HCF of two numbers can be calculated using the division method. Let us understand this using the following steps and the example given below.

• Step 1: In this method, we divide the larger number by the smaller number and check the remainder.
• Step 2: Then, we make the remainder of the previous step as the new divisor; and the divisor of the previous step becomes the new dividend. After this, we perform the long division again.
• Step 3: We continue the long division process till we get the remainder as 0. It should be noted that the last divisor will be the HCF of those two numbers.

Example: Find the HCF of 198 and 360 using the division method.

Solution: Let us find the HCF of the given numbers using the following steps.

• Step 1: Among the two given numbers, 360 is the larger number, and 198 is the smaller number.
• Step 2: We divide 360 by 198 and check the remainder. Here, the remainder is 162. Make the remainder 162 as the new divisor and the previous divisor 198 as the new dividend and perform the long division again.
• Step 3: We will continue this process till we get the remainder as 0. Here, the last divisor is 18 which is the HCF of 198 and 360. Therefore, the HCF of 198 and 360 is 18.

HCF of Multiple Numbers

The method to find the HCF of multiple numbers is the same when we use the 'listing factors method' and 'the prime factorization method'. However, while using the division method, there is a slight change in the case of multiple numbers. Let us learn how to find the HCF of three numbers using the division method.

HCF of Three Numbers

In order to find the HCF of three numbers, we use the following procedure. Let us understand this using the steps and the example given below.

• Step 1: First, find the HCF of the largest and the smallest of the given numbers.
• Step 2: Then, find the HCF of the third number and the HCF obtained from the first two numbers in the previous step.
• Step 3: This gives the HCF of the three numbers.

Example: Find the HCF of 126, 162, and 180.

Solution: First, we will find the HCF of the two numbers 126 and 180. The HCF of 126 and 180 = 18. Then, we will find the HCF of the third number, which is 162, and the HCF of the two numbers obtained in the previous step, that is, 18. This will give the final HCF of all the three numbers.

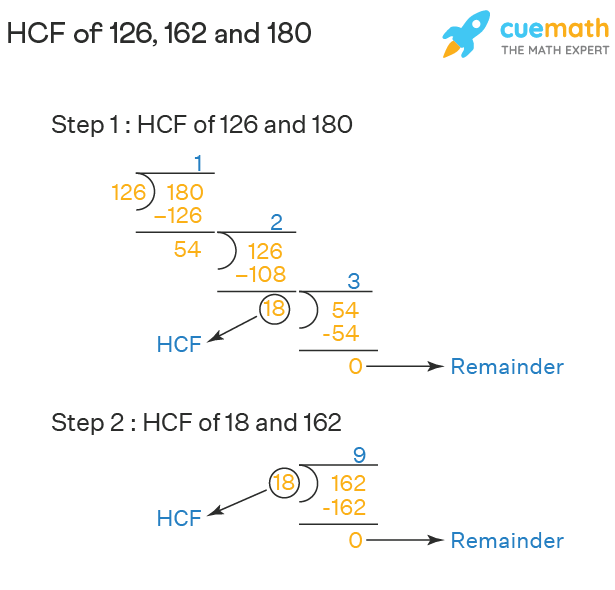
Therefore, HCF of 126, 162 and 180 = 18

HCF of Four Numbers

To find the HCF of four numbers, we use the following steps.

• Step 1: First, we will find the HCF of the two pairs of numbers separately.
• Step 2: Then, we will find the HCF of the HCFs that were calculated in the previous step.

HCF of Prime Numbers

We know that a prime number has only two factors, 1 and the number itself. Let us consider two prime numbers 2 and 7, and find their HCF by listing their factors. The factors of 2 = 1, 2; and the factors of 7 = 1, 7. We can see that the only common factor of 2 and 7 is 1. Hence, the HCF of prime numbers is always equal to 1.

Properties of HCF

We already know that the HCF of a and b is the highest common factor of the numbers a and b. Let us have a look at the important properties of HCF:

• The HCF of two or more numbers divides each of the numbers without a remainder.
• The HCF of two or more numbers is a factor of each of the numbers.
• The HCF of two or more numbers is always less than or equal to each of the numbers.
• The HCF of two or more prime numbers is 1 always.

The HCF of two or more numbers is the highest common factor of the given numbers. It is found by multiplying the common prime factors of the given numbers. Whereas the Least Common Multiple (LCM) of two or more numbers is the smallest number among all common multiples of the given numbers.
Let us assume 'a' and 'b' are the two numbers. Therefore, the formula that expresses the relationship between their LCM and HCF is given as:

LCM (a,b) × HCF (a,b) = a × b

Let us understand this relationship with an example.

Example: Let us find the HCF and LCM of 6 and 8 to understand their relationship.

Solution: The HCF of 6 and 8 = 2; The LCM of 6 and 8 = 24; The product of the two given numbers is 6 × 8 = 48. So, let us substitute these values in the formula that explains the relationship between the LCM and HCF of two numbers. On substituting the values in the formula, LCM (a,b) × HCF (a,b) = a × b, we get, 24 × 2 = 48.

☛ Related Articles

• HCF of 24 and 32
• HCF of 2 and 4
• HCF of 336 and 54
• HCF of 825, 675, and 450
• HCF of 135 and 225
• HCF of 196 and 38220
• HCF of 65 and 117
• HCF of 4 and 6
• HCF of 616 and 32
• HCF of 403, 434 and 465
• HCF of 20 and 30
• HCF of 18 and 24
• HCF of 867 and 225
• HCF of 12 and 18

Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12. Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.

 

What is HCF in Math?

The HCF (Highest Common Factor) of two numbers is the highest number among all the common factors of the given numbers. For example, the HCF of 12 and 36 is 12 because 12 is the highest common factor of 12 and 36.

How to find the HCF of Two Numbers?

There are 3 methods to calculate the HCF of two numbers:

• HCF by the listing factors method
• HCF by prime factorization
• HCF by division method

These methods are explained in detail with examples under the section How to find HCF? on this page.

What are the Properties of HCF?

The properties of HCF are listed as follows:

• The HCF of two or more numbers divides each of the numbers without a remainder.
• The HCF of two or more numbers is a factor of each of the numbers.
• The HCF of two or more numbers is always less than or equal to each of the numbers.
• The HCF of two or more prime numbers is 1 always.

How to find HCF by Division Method?

The steps to find the HCF of two numbers using long division are mentioned below:

• Step 1: In this method, we divide the larger number by the smaller number and check the remainder.
• Step 2: Then, we make the remainder of the previous step as the new divisor and the divisor of the previous step becomes the new dividend. After this step, we perform the long division again.
• Step 3: We continue the long division process till we get the remainder as 0. It should be noted that the last divisor will be the HCF of those two numbers.

What is the Difference Between HCF and LCM?

The Least Common Multiple (LCM) of two or more numbers is the smallest number among all the common multiples of the given numbers and the HCF (Highest Common Factor) of two or more numbers is the highest number among all the common factors of the given numbers.

What is the Relationship between HCF and LCM of two Numbers?

The formula that expresses the relationship between the Least Common Multiple (LCM) and HCF is given as, LCM (a,b) × HCF (a,b) = a × b; where 'a' and 'b' are the two numbers.

What is the HCF of two Consecutive Natural Numbers?

The HCF of two consecutive natural numbers is 1. This is due to the fact that there is no common factor between any two consecutive numbers other than 1. Therefore, 1 is always the HCF between two consecutive numbers.

What is the HCF of two Co-prime Numbers?

Co-prime numbers are those numbers whose common factor is only 1. These need not necessarily be prime numbers. For example, (4 and 7) and (8 and 15) are co-prime numbers. Since Co-prime numbers have only 1 as their highest common factor, their HCF is always 1.

What is the HCF of two Consecutive Even Numbers?

The HCF of two consecutive even numbers is always 2. We know that the HCF (Highest Common Factor) of two or more numbers is the highest number among all the common factors of the given set of numbers. For example, the HCF of 6 and 8 is 2, the HCF of 14 and 16 is also 2.

How to Find the HCF of 3 Numbers?

To find the HCF of three numbers, we use the following steps. Let us find the HCF of 4, 6, and 8 to understand the steps.

• Step 1: First, find the HCF of the largest and the smallest of the given numbers. Here, the HCF of 4 and 8 is 4.
• Step 2: Then, find the HCF of the third number and the HCF of the first two numbers which was obtained in the previous step. This means we need to find the HCF of 4 and 6. So, the HCF 4 and 6 is 2. This will be considered to be the HCF of the given numbers.
• Step 3: Therefore, the HCF of 4, 6, and 8 is 2.

How to find HCF by Prime Factorization?

In order to find the HCF of numbers by prime factorization, we use the following steps. For example, let us find the HCF of 24 and 36.

• Step 1: Find the prime factors of the given numbers. In this case, the prime factors of 24 = 2 × 2 × 2 × 3 or 2³ × 3, the prime factors of 36 = 2 × 2 × 3 × 3 or 2² × 3² . The HCF of these two numbers will be the product of the common factors that have the smallest power.
• Step 2: Here, the common prime factors that have the smallest power are 2² and 3. So, 2² × 3 = 12.
• Step 3: Therefore, the HCF of 24 and 36 is 12.

Why is HCF Important?

HCF is important because it is used to split something into small sections, to distribute items to larger groups, or to arrange something into groups.