Co-prime Numbers

Co-prime numbers are the numbers whose common factor is only 1. There should be a minimum of two numbers to form a set of co-prime numbers. Such numbers have only 1 as their highest common factor, for example, {4 and 7}, {5, 7, 9} are co-prime numbers. Co-prime numbers need not be prime numbers always. Two composite numbers like 4 and 9 also form a pair of co-primes.

If the only common factor of two numbers a and b is 1, then a and b are co-prime numbers. In this case, (a, b) is said to be a co-prime pair. Co-prime numbers are also referred to as relatively prime or mutually prime numbers.

List of Co-prime Numbers

Given below is the list of few co-prime numbers for your reference.

To find whether any two numbers are co-prime, we first find their GCF. If their GCF is 1, we can say that they are co-prime.

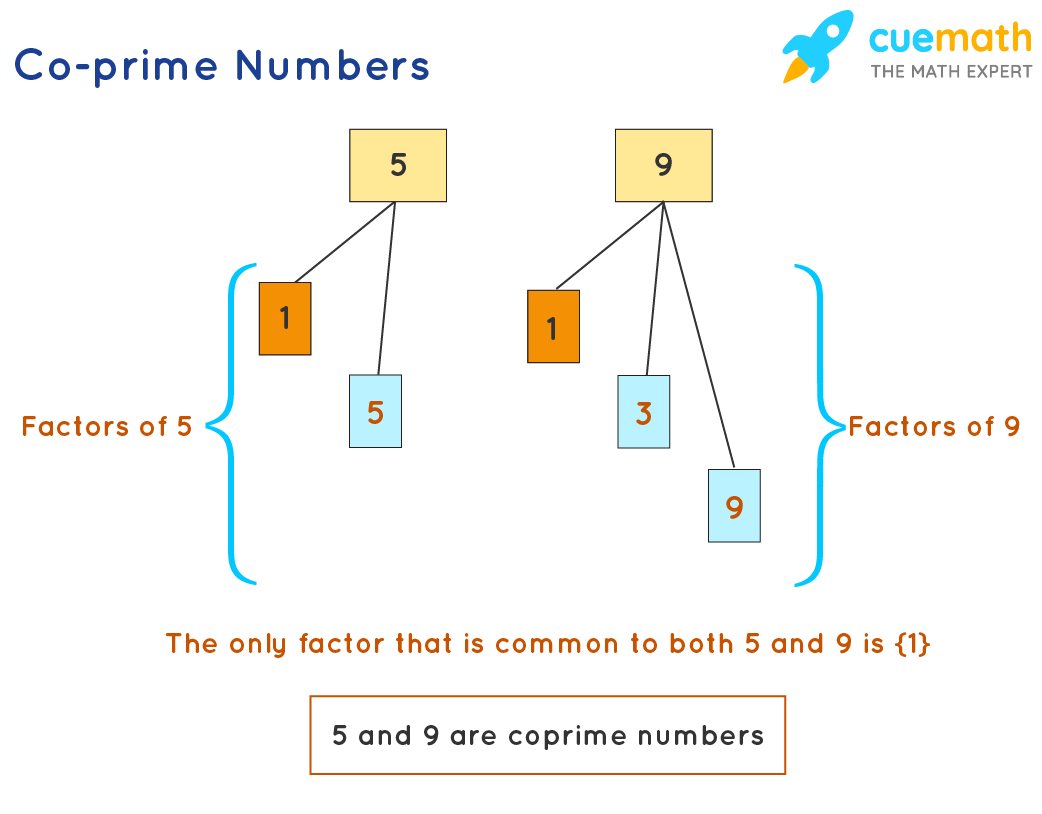
Example 1: Let us consider two numbers 5 and 9. The factors of 5 are 1 and 5. The factors of 9 are 1, 3, and 9. The factor that is common to both 5 and 9 is 1. GCF of (5, 9) = 1. Thus, (5, 9) is a co-prime pair.

Example 2: Let us consider two numbers 6 and 10. The factors of 6 are 1, 2, 3, and 6. The factors of 10 are 1, 2, 5, and 10. Factors that are common to both 6 and 10 are 1 and 2. So GCF (6, 10) = 2. Thus, (6, 10) is NOT a co-prime pair.

Co-prime numbers can be identified easily with the help of some properties that are explained below:

• The HCF of two coprime numbers is always 1. For example, 5 and 9 are coprime numbers, there, HCF (5, 9) = 1.
• The LCM of two co-prime numbers is always their product. For example, 5 and 9 are co-prime numbers. Hence, LCM (5, 9) = 45.
• 1 forms a co-prime number pair with every number.
• Two even numbers cannot be co-prime numbers as they always have 2 as the common factor.
• The sum of two co-prime numbers is always co-prime with their product. For example, 5 and 9 are co-prime numbers. Here, 5 + 9 = 14 is co-prime with 5 × 9 = 45.
• Two prime numbers are always co-prime. They have only 1 as their common factor. Consider 29 and 31. 29 has 2 prime factors, 1 and 29 only. 31 has 2 prime factors, 1 and 31 only. 29 and 31 are prime numbers. They have only one common factor 1. Thus they are co-prime. We can check any two prime numbers and get them as co-prime. For example, 2 and 3, 5 and 7, 11 and 13, and so on.
• All pairs of two consecutive numbers are co-prime numbers. Any two consecutive numbers have 1 as their common factor.

Consider a few pairs of such numbers. Let us try with 14 and 15.

There are multiple such combinations as 1 is the only common factor.

Co-prime numbers are those whose HCF is 1 or two numbers whose only common factor is 1 are known as co-prime numbers. On the other hand, twin prime numbers are those prime numbers whose difference is always 2. For example, 3 and 5 are twin prime numbers.

• Twin numbers are always prime numbers while co-prime numbers can be composite numbers as well.
• The difference between two twin primes is always 2 while the difference between two co-primes can be any number.
• All the pairs of twin prime numbers are also co-prime, while all co-prime numbers may or may not be twin primes.
• 1 forms a co-prime pair with every number, while it forms twin prime pair with only 3.

In the list of co-prime numbers from 1 to 100, there are so many pairs that can be listed as co-prime numbers based on the above properties. Some of the co-prime number pairs that exist from 1 to 100 are (1, 2), (3, 67), (2, 7), (99, 100), (34, 79), (54, 67), (10, 11), etc. Try out forming more such pairs of co-prime numbers by yourself. Here is Cuemath's online co-prime calculator for our ease.

Important Notes:

• Two numbers are co-prime if their GCF is 1 and vice versa.
• Co-prime numbers don't need to be prime numbers. For example, 12 and 35 are co-prime numbers. However, 12 and 35 are NOT prime numbers.

Tips and Tricks:

• Any two prime numbers are co-prime.
• Any two consecutive numbers are co-prime.
• 1 forms a co-prime pair with any other number.
• A prime number is co-prime with any other number that is not it's multiple.
• Two even numbers are NEVER co-prime.

☛ Related Topics on Co-prime Numbers

Check out few more interesting articles related to co-prime numbers for better understanding.

• HCF of 2 Co-prime Numbers
• Is 2 a Prime Number?
• Is 41 a Prime Number?
• Co-prime Calculator

What are Co-prime Numbers in Math?

If the only factor of two numbers a and b is 1, then a and b are co-prime numbers. It is difficult to determine the co-prime numbers list. But you can try to generate the one using the above theory.

What is the Difference Between Prime and Co-prime Numbers?

A prime number is a number that is greater than 1 which has exactly two factors 1 and itself. Co-prime numbers are numbers whose HCF (Highest Common Factor) is 1.

How to Find the Co-prime of a Number?

The HCF of two co-prime numbers is 1. Thus, to find the co-prime number of a number, it is sufficient to find a number that is NOT divisible by any of the factors of the given number.

Which Numbers are Identified as Co-prime Numbers?

A single number cannot be co-prime. Two numbers are said to be co-prime if their HCF is 1.

Are 18 and 35 Co-prime Numbers?

The factors of 18 are 1, 2, 3, 6, 9, 18. The factors of 35 are 1, 5, 7, 35. Here, 18 and 35 have no common factor other than 1. Thus, 18 and 35 are co-prime.

Are Co-prime Numbers Always Prime Numbers?

No, co-prime numbers don't have to be prime numbers. For example, 18 and 25 are co-prime numbers as their HCF is 1. But 18 and 25 are NOT prime numbers.

What is the HCF of Two Co-prime Numbers?

HCF of two co-prime numbers is always 1. As 1 is the only common factor of two co-prime numbers.

Are Twin Prime Numbers Always Co-prime?

Yes. Twin prime numbers are always co-prime as they are a pair of even numbers and even numbers have only 1 as the common factor.