A day full of math games & activities. Find one near you.

Factors of 180

180, a positive integer with more divisors than any other smaller positive integer, is also a highly composite number. 180 is a number which is refactorable. In this lesson, we will calculate the factors of 180, prime factors of 180, and factors of 180 in pairs along with solved examples for a better understanding.

Factors of 180: 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, and 180
Prime Factorization of 180: 180 = 2² × 3²× 5

1.	What Are the Factors of 180?
2.	How to Calculate the Factors of 180?
3.	Factors of 180 by Prime Factorization
4.	Factors of 180 in Pairs
5.	Important Notes
6.	FAQs on Factors of 180

What Are the Factors of 180?

The number 180 is an even composite number. As it is even, it will have 2 as its factor. To understand why it is composite, let's recall the definition of a composite number. A number is said to be composite if it has more than two factors. Consider the number 19. It has only two factors, 1 and 19. So, it's prime. Now, let's take the case of 60. The factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60. There are more than two factors of 60, hence it's composite. Let's come back to 180. The factors of 180 are all the integers that 180 can be divided into.

How to Calculate the Factors of 180?

We can use different methods like prime factorization and the division method to calculate the factors of 180. In prime factorization, we express 180 as a product of its prime factors and in the division method, we see what numbers divide 180 exactly without a remainder.

Factors of 180 by Prime Factorization

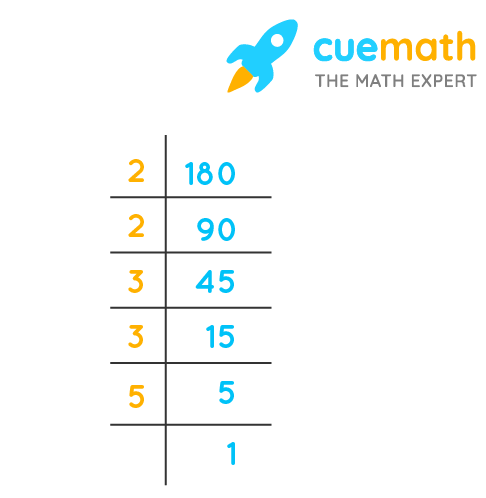
The number 180 is divided by the smallest prime number which divides 180 exactly, i.e., it leaves a remainder of 0. The quotient is then divided by the smallest or second smallest prime number and the process continues till the quotient gets undividable. Let us divide 180 by the prime number 2.

180 ÷ 2 = 90

Now we need to divide the quotient 90 by the next least prime number.

90 ÷ 2 = 45

Now, 45 is a odd number so it is not divisible by 2, but it is divisible by 3.

45 ÷ 3 = 15

Again 15 is divisible by 3.

15 ÷ 3 = 5

5 is a prime number we cannot divide further. Therefore, the prime factors of 180 are 2, 3, and 5 only. Exponentially it can be written as 180 = 2² x 3² x 5

Factors of 180 by prime factorization

Explore factors using illustrations and interactive examples.

Factors of 80 - The factors of 80 are 1, 2, 4, 5, 8, 10, 16, 20, 40, and 80.
Factors of 90 - The factors of 90 are 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, and 90.
Factors of 108 - The factors of 108 are 1, 2, 3 , 4, 6, 9, 12, 18, 27, 36, 54, and 108.
Factors of 40 - The factors of 40 are 1, 2, 4, 5, 8, 10, 20, and 40.
Factors of 192 - The factors of 192 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, and 192.

Factors of 180 in Pairs

The pairs of numbers which give 180 when multiplied are known as factor pairs of 180. The following are the factors of 180 in pairs or factor pairs of 180 can be given as

The product as 180	Pair factor
1 × 180 = 180	(1, 180)
2 × 90 = 180	(2, 90)
3 × 60 = 180	(3, 60)
4 × 45 = 180	(4, 45)
5 × 36 = 180	(5, 36)
6 × 30 = 180	(6, 30)
9 × 20 = 180	(9, 20)
10 × 18 = 180	(10, 18)
12 × 15 = 180	(12, 15)
15 × 12 = 180	(15, 12)
18 × 10 = 180	(18, 10)
20 × 9 = 180	(20, 9)
30 × 6 = 180	(30, 6)
36 × 5 = 180	(36, 5)
45 × 4 = 180	(45, 4)
60 × 3 = 180	(60, 3)
90 × 2 = 180	(90, 2)
180 × 1 = 180	(180, 1)

Observe in the table above, after 12 × 15, the factors start repeating except the order. So, it is enough to find factors until (12,15).

If we consider negative integers, then both the numbers in the pair factors will be negative.
36 is positive and - ve (×) - ve = +ve.
So, we can have factor pairs of 180 as (-1,-180) ; (-2,-90); (-4,-45); (-5,-36) ; (-6,-30) ; (-9, -20); (-10,-18) ; (-9, -20).

Pair factors of 180

Important Notes:

The numbers which we multiply to get 180 are the factors of 180.
Factors of 180 are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, and 180.
Factor pairs of 180 are (1,180) (2, 90) (3, 60) (4,45) (5, 36) (6, 30) (9, 20) (10, 18 ) and (12, 15).

Do you know 180 is a refactorable number?
Do you know 180 is an abundant number, with its proper divisors summing up to 366?

Example 1: Can you help Lisa list the factors of 180 and find the factor pairs?

Solution:

The factors of 180 are the numbers that divide without any remainder.
They are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, and 180.
Factors pairs are the pairs of two numbers which, when multiplied, give 180.
- 1 × 180 = 180
- 2 × 90 = 180
- 3 × 60 = 180
- 4 × 45 = 180
- 5 × 36 = 180
- 6 × 30 = 180
- 9 × 20 = 180
- 10 × 18 = 180
Factors of 180 are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, and 180.
Factor pairs of 180 are (1,180), (2,90), (3, 60), (4,45), (5, 36), (6, 30), (9, 20), (10, 18), and (12, 15).
Example 2: Joel has to list the factors of 180 and the factors of 120 and find the common factors between them. Can you help him do it?

Solution:

Factors of 120 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, and 120.
Factors of 180 are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, and 180.
We can see that 1, 2, 5, 10, 12, 15, 20, 30, and 60 are the common factors of 120 and 180.
Therefore, common factors of 120 and 180 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60.

Example 3: The area of a rectangle is 180 square inches. List all the possible combinations possible for length and breadth.

Solution:

Area of rectangle = length × breadth
Given the area is 180 square inches, the possible length and breadth are the factors of 180.
There are 18 possible combinations.
We can swap the values of length and breadth.

Length	Breadth
1 in	180 in
2 in	90 in
3 in	60 in
4 in	45 in
5 in	36 in
6 in	30 in
9 in	20 in
10 in	18 in
12 in	15 in
15 in	12 in
18 in	10 in
20 in	9 in
30 in	6 in
36 in	5 in
45 in	4 in
60 in	3 in
90 in	2 in
180 in	1 in

go to slide go to slide go to slide

Want to build a strong foundation in Math?

Go beyond memorizing formulas and understand the ‘why’ behind them. Experience Cuemath and get started.

Book a Free Trial Class

go to slide go to slide

FAQs on Factors of 180

What are the factors of 180?

Factors of 180 are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, and 180.

What are all the factors pair of 180?

Factor pairs of 180 are (1,180), (2,90), (3, 60), (4,45), (5, 36), (6, 30), (9, 20), (10, 18), and (12, 15).

Is 180 a perfect square?

180 is not a perfect square number because its square root is not a whole number.

What are the factors of 180 between 50 and 100?

The factors of 180 between 50 and 100 are 60 and 90 only.

What are the negative factors of 180?

-1, -2, -3, -4, -5, -6, -9, -10, -12, -15, -18, -20, -30, -36, -45, -60, -90, and -180.

Math worksheets and
visual curriculum